
- •2. Оптика кристаллов
- •2.1. Описание анизотропной среды
- •2.2. Структура плоской гармонической волны в кристалле
- •2.3. Уравнение Френеля
- •2.4. Лучевой и волновой эллипсоиды Френеля
- •2.5. Лучевая поверхность
- •2.6. Одноосные кристаллы
- •2.7. Двойное лучепреломление
- •2.8. Поляризационные элементы
- •2.9. Искусственная анизотропия
- •2.10. Задачи и примеры
2. Оптика кристаллов
2.1. Описание анизотропной среды
В
этом разделе будут рассмотрены особенности
прохождения света через среду,
обладающую электрической анизотропией.
В естественных условиях к таким
средам относятся прежде всего кристаллы.
Для подобных сред материальные
уравнения, связывающие векторы
![]() и
и
![]() ,
имеют вид, отличный от используемых для
изотропных сред (
,
имеют вид, отличный от используемых для
изотропных сред (![]() ):
):
 (2.1)
(2.1)
Девять
величин
![]() ;
;
![]() образуют тензор диэлектрической
проницаемости анизотропной среды.
В более компактной форме выражения
(2.1) можно записать так:
образуют тензор диэлектрической
проницаемости анизотропной среды.
В более компактной форме выражения
(2.1) можно записать так:
![]() ,
, ![]() (2.2)
(2.2)
Плотность электрической энергии в среде выражается формулой
![]() . (2.3)
. (2.3)
Изменяя
обозначения индексов суммирования (![]() ),
запишем выражение (2.3) в виде
),
запишем выражение (2.3) в виде
![]() ; (2.4)
; (2.4)
вычитая почленно (2.3) из (2.4), получим
![]() .
.
Поскольку
проекции
![]() ,
,
![]() независимы и в общем случае не равны
нулю, из последнего выражения заключаем,
что
независимы и в общем случае не равны
нулю, из последнего выражения заключаем,
что![]() ,
т.е. тензор диэлектрической проницаемости
симметричен. Как известно из курса
математики, такой тензор поворотом
системы координат может быть приведен
к диагональному виду, тогда в этой
системе координат связь между векторами
и
примет наиболее простой вид:
,
т.е. тензор диэлектрической проницаемости
симметричен. Как известно из курса
математики, такой тензор поворотом
системы координат может быть приведен
к диагональному виду, тогда в этой
системе координат связь между векторами
и
примет наиболее простой вид:
![]() . (2.5)
. (2.5)
Такую
систему координат в кристалле называют
системой главных диэлектрических осей,
а соответствующие значения
![]() ,
,![]() и
и
![]() - главными диэлектрическими проницаемостями
кристалла. В этой системе объемная
плотность электрической энергии может
быть выражена двумя различными и
наиболее простыми формулами:
- главными диэлектрическими проницаемостями
кристалла. В этой системе объемная
плотность электрической энергии может
быть выражена двумя различными и
наиболее простыми формулами:
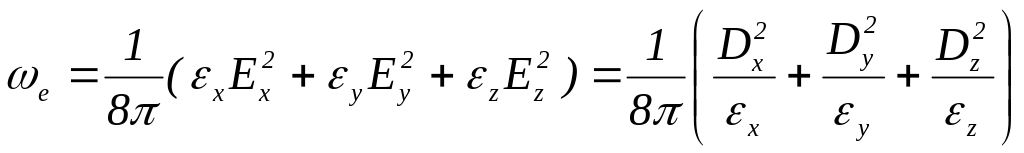 . (2.6)
. (2.6)
В
 Рис.8
Рис.8
2.2. Структура плоской гармонической волны в кристалле
Рассмотрим
плоскую гармоническую волну с частотой
![]() ,
распространяющуюся в кристалле в
направлении
,
распространяющуюся в кристалле в
направлении
![]() .
Тогда векторы
,
,
.
Тогда векторы
,
,![]() и
и
![]() такой волны можно записать в виде
такой волны можно записать в виде
![]() ,
, ![]() ,
, ![]() ,
,
(2.7)
,
,
(2.7)
где
![]() ,
,
![]() ,
,
![]() - амплитуды волн;
- амплитуды волн;
![]() - пространственно-временной параметр,
характеризующий плоскую волну (фаза
волны).
- пространственно-временной параметр,
характеризующий плоскую волну (фаза
волны).
Подставим
выражения (2.7) в уравнения Максвелла (
1.1) - (1.4), при этом учтем, что действие
операторов
![]() и
и
![]() на векторы поля равносильно умножению
на эти векторы величин
на векторы поля равносильно умножению
на эти векторы величин
![]() и
и
![]() соответственно. Тогда после
преобразований получим
соответственно. Тогда после
преобразований получим
![]() (2.8)
(2.8)
где
![]() - показатель преломления.
- показатель преломления.
Из
уравнения (2.8) видно, что вектор
и, следовательно, вектор
![]() перпендикулярны векторам
,
и
,
которые поэтому должны быть компланарны.
Кроме того, вектор
ортогонален
.
Следовательно, векторы
и
перпендикулярны к направлению
распространения волны
,
а вектор
составляет с ним некоторый угол, в
общем случае отличный от прямого (рис.
9).
перпендикулярны векторам
,
и
,
которые поэтому должны быть компланарны.
Кроме того, вектор
ортогонален
.
Следовательно, векторы
и
перпендикулярны к направлению
распространения волны
,
а вектор
составляет с ним некоторый угол, в
общем случае отличный от прямого (рис.
9).
Н
Рис.9
![]() .
.
Введем
единичный вектор
![]() ,
характеризующий это направление,
тогда получим, что векторы
,
и
с одной стороны, и
,
и
,
характеризующий это направление,
тогда получим, что векторы
,
и
с одной стороны, и
,
и
![]() -с другой, образуют ортогональные тройки
векторов с общим вектором
,
повернутые относительно друг друга на
угол
-с другой, образуют ортогональные тройки
векторов с общим вектором
,
повернутые относительно друг друга на
угол
![]() .
Таким образом, в анизотропной среде
в отличие от изотропной направление
распространения энергии (луча)
не совпадает с направлением распространения
волнового фронта
.
Вместе с тем равенство плотностей
электрической и магнитной энергий
сохраняется. Действительно, из (2.8)
получим
.
Таким образом, в анизотропной среде
в отличие от изотропной направление
распространения энергии (луча)
не совпадает с направлением распространения
волнового фронта
.
Вместе с тем равенство плотностей
электрической и магнитной энергий
сохраняется. Действительно, из (2.8)
получим
![]() ;
; ![]() ,
,
откуда
видно, что, согласно свойствам смешанного
произведения векторов,
![]() .
Полная плотность электромагнитной
энергии
.
Полная плотность электромагнитной
энергии
![]() .(2.9)
.(2.9)
Из последнего выражения получим
![]() , (2.10)
, (2.10)
где
![]() - фазовая скорость волны.
- фазовая скорость волны.
Сравнив (2.10) и (1.13), можно заметить, что величина
![]() (2.11)
(2.11)
характеризует
скорость распространения энергии;
поэтому она называется групповой,
или лучевой, скоростью. Очевидно, что
отношение
![]() определяет лучевой, или групповой,
показатель преломления, который
связан с фазовым как
определяет лучевой, или групповой,
показатель преломления, который
связан с фазовым как
![]() .
.
