Понятие амплитудно-фазовой частотной характеристики и ее взаимосвязь с остальными частотными характеристиками.
Амплитудно-фазовая частотная характеристика (АФЧХ) есть отношение выходного и входного гармонического сигна-лов, записанных в комплексной форме, при изменении часто-ты входного сигнала от нуля до бесконечности:
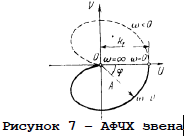
АФЧХ изображается на комплексной плоскости и для каж-дой частоты представляет собой вектор длиной A(ω), идущий под углом ψ(ω) к вещественной положительной полуоси. Го-дограф, соединяющий концы векторов, построенных для всех частот от нуля и до бесконечности, и будет являться АФЧХ.
Амплитудно-фазовая частотная характеристика (ее еще называют комплексной передаточной функцией) звена получа-ется из передаточной функции W(p) подстановкой p=jω:
Амплитудно-фазовая частотная характеристика представ-ляет собой комплексное число и может быть представлена в виде:
где
– амплитудно-частотная характеристика;
U(ω) - вещественная частотная характеристика;
V(ω) - мнимая частотная характеристика.
Если передаточная функция представлена в виде отноше-ния полиномов числителя и знаменателя, то модуль ампли-тудно-фазовой характеристики удобно находить как отношение модулей числителя и знаменателя:
а фазу - как разность аргументов числителя и знаменателя
Графически амплитудно-фазовая частотная характеристи-ка изображается на комплексной плоскости (рисунок 7) в координатах (U, V), как годограф функции W(jω). Можно строить амплитудно-фазовую частотную характеристику, вы-делив в выражении W(jω) вещественную и мнимую части. При этом частоту ω изменяют от 0 до ∞ (сплошная кривая на ри-сунке 7) или же от —∞ до +∞, когда добавляется еще сим-метричная к ней пунктирная кривая.
Прямое и обратное преобразование Лапласа.
Преобразование Лапласа выполняется в соответствии с формулой:
где f(t) - оригинал функции;
F(p) - изображение функции по Лапласу.
Переход от оригинала к изображению называется прямым преобразовании Лапласа и имеет символическую запись:
Переход от изображения к оригиналу называется обрат-ным преобразованием Лапласа и имеет символическую запись:
На практике прямое и обратное преобразования осущест-вляются по таблицам изображений типовых функций.
Регулировочная характеристика.
Уравнение статики позволяет исследовать зависимость скорости вращения двигателя ωдв (или нагрузки) от величины подводимого к якорю управляющего напряжения Uтп и момента сопротивления нагрузки Mс в установившемся режиме. Статические характеристики ωдв=f(uтп) при Mс=const и ωдв=f(Mс) при Uтп=const называют соответственнорегулировочной и механической.
Для определения регулировочной характеристики перепишем уравнение статики, выделив напряжение тиристорного преобразователя в «чистом» виде:
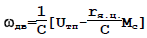
В этом выражении коэффициент 1/С [рад/В⋅с] показывает, на сколько изменяется скорость вращения двигателя при изменении управляющего напряжения на одну единицу. Поэтому коэффициент 1/С =kдв называют еще коэффициентом
преобразования двигателя.
Обозначим
теперь
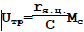где
rя.ц.
—
сопротивление
якорной
цепи (Ом); Mс
—
момент сопротивления нагрузки
(Н⋅м),
С
-
постоянная двигателя [Н⋅м/А].
Следовательно, Uтр
измеряется
в вольтах, а так как при Mс≠0
двигатель
вращается только при выполнении условия:
То величину Uтр называют напряжением трогания. Таким образом, регулировочная характеристика двигателя может быть записана в виде ωдв=kдв(Uтп-Uтр) при
Uтп>Uтр, если двигатель вращается в одну сторону. При изменении знака управляющего напряжения меняется и направление вращения двигателя. Тогда
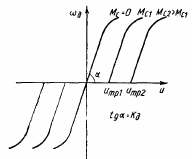
По полученным формулам строятся регулировочные характеристики для различных значений момента сопротивления нагрузки, учитывая, что при больших токах якоря (больших значениях напряжения Uтп) в характеристиках может появиться ограничение, вызываемое реакцией якоря. Возможный вид регулировочных характеристик показан на рисунке 5, а, из которого видно, что наличие момента
сопротивления приводит к появлению зоны статической нечувствительности тем большей, чем больше момент Мс. Зона нечувствительности меньше у двигателей, имеющих малое сопротивление обмотки якоря и большую токовую постоянную С.
