Шпоры по вычислительной математике

1. Численное дифференцирование функции одной переменной.

Пусть на отрезке задана функция в некоторой системе точек:

,

где . Известно, что у этой функции есть производные всех порядков. Требуется найти в некоторой точке ту или иную производную функции .

Первый способ решения этой задачи напрашивается сам по себе: заменим функцию ее многочленом Лагранжа, построенным по заданной таблице значений функции, а потом возьмем требуемую производную от него, пользуясь особой простотой строения многочлена в смысле правил дифференцирования.

Второй способ предполагает, что точка, в которой надо найти производную, является одним из узлов таблицы, например, . Тогда в качестве искомой первой производной берется число

.

По этому принципу можно вычислить в точках . Затем по первым производным и прежнему принципу можно найти в точках затем - - в точках и т.д.

6,17. Численное интегрирование функции одной переменной.

Требуется найти

с той или иной степенью точности. Известны три классических способа сделать это.

Способ № 1: метод прямоугольников. Отрезок разбивается на равных частей: длиной , где

.

Затем на каждом участке функция заменяется на константу , после чего искомый интеграл заменяется на интеграл от новой ступенчатой функции, т.е. на число

.

Можно доказать, что справедлива следующая оценка:

,

где - максимум модуля первой производной функции на отрезке .

Способ № 2: метод трапеций.

В этом методе искомый интеграл после разбиения отрезка на равные части заменяется на следующую сумму (суммируются площади трапеций, а не прямоугольников, как в предыду-щем случае):

,

где Можно доказать, что если - исходный обсуждаемый интеграл,то

,

где на отрезке .

: Способ № 3: метод парабол(Cимпсона). В этой ситуации отрезок разбивается на равных частей: , где . На участках , функцию заменяют на параболу, проходящую через точки и интегралом от этой параболы на участке заменяют интеграл от функции на этом же участке, после чего все эти интегралы суммируют и результаты принимают за интеграл от по всему отрезку . Полученная приближенная формула называется формулой парабол или формулой Симпсона. Вот ее окончательный

вид:

.

Если левую часть этого приближенного равенства обозначить через I а правую – через S, то окажется выполненной следующая формула для оценки погрешности:

,

где - максимум на интервале четвертой производной функции .

19, 21. Погрешности вычислений. Устойчивость и экономичность алгоритма.

Реальное проведение любых вычислений проводится над числами, которые задаются не только точно, но и приближенно. Например, запись 7/3 обозначает число, но записать его в виде десятичной дроби можно только приближенно. Если же вычисления проводятся на компьютере, то приближенно записывать приходится не только числа типа 7/3, но многие другие. В результате возникают ошибки, которые постепенно накапливаются и искажают результат.

К настоящему времени все программные средства, благодаря которым на компьютерах проводятся вычисления, устроены так, что точность проводимых расчетов можно регулировать программно. Можно, например, «поручить» компьютеру вести вычисления с точностью до трех знаков после десятичной запятой; определение точности результата в этом случае может оказаться сложнейшей математической задачей. В некоторых случаях полученный результат можно запросить заново с большей точностью или оставить без изменения.

Алгоритм, по которому ведутся вычисления, может быть устойчивым к приближенным числам и может не быть таковым. Слова «устойчивый алгоритм» означают, что чем точнее задаются числа для обработки, тем точнее получается результат, причем для любой точности результата можно указать такую точность обрабатываемых чисел, что алгоритм приведет к результату именно с этой заданной точностью. В последующем мы столкнемся именно с такой ситуацией при изучении метода итераций для решения систем линейных алгебраических уравнений. Примером метода, который не является устойчивым к приближенным числам, является метод последовательного исключения неизвестных для решения тех же систем. Одну из его реализаций мы рассмотрим в ближайшее время.

И последнее. Алгоритм, реализующий те или иные вычисления, может требовать различное время для своей работы. Чем большего времени требует алгоритм, тем более высокую сложность по времени он имеет. Точно так же, чем больше компьютерной памяти требуется для реализации алгоритма, тем более высокую сложность по памяти он имеет.

12. Задача аппроксимации функции.

Пусть на отрезке [a,b] некоторая функция f(x) задана лишь в некоторых точках , т.е. известны ее значения , которые, как правило, собирают в таблицу:

Кроме того, пусть задана некоторая точка . Задача аппроксимации функции состоит в том, чтобы по имеющейся таблице найти число с известной степенью точности. Слово «аппроксимация» означает «приближение».

Легко понять, что если на функцию не накладываются никакие дополнительные условия, то постановка задачи бесперспективна. Мы будем далее предполагать, что функция обладает всеми производными. Оказывается, что в этом случае по имеющимся n+1 значениям можно найти еще одно и оценить, насколько оно точно.

Для осуществления равномерного приближения должна быть задана не только таблица, но и некоторый класс функций G внутри которого и будет выделена функция . Введем величину

,

в которой числа берутся из таблицы, а числа для каждой функции из класса G предполагаются вычислимыми. Функция выбирается как доставляющая минимум величине . Эту функцию называют наилучшим равномерным приближением функ-ции из класса G. Конечно, как оценить разность в такой ситуации, - это от-дельная тема, тесно связанная как с природой класса G, так и с таблицей.

Предположим, что класс G представляет собой множество всех многочленов степени не превосходящей некоторого конкретного числа m. Тогда задача равномерного приближения функций приобретает следующий вид:

среди многочленов найти такой, при котором величина

принимает минимальное значение.

Для этого надо найти такие , при которых функция

принимает минимальное возможное значение, а это происходит тогда, когда равны нулю все ее частные производные:

это - система из m+1линейных алгебраических уравнений с m+1 неизвестными ; можно доказать, что эта система всегда совместна и определенна. Ее решение и есть искомый многочлен.

Распишем эту систему в традиционной форме, раскрыв скобки и приведя подобные

члены:

;

включив процедуру решения систем линейных алгебраических уравнений теперь легко получить ответ.

10. Полиномиальная интерполяция. Полином Логранжа.

Пусть на отрезке [a,b] некоторая функция f(x) задана лишь в некоторых точках , т.е. известны ее значения , которые, как правило, собирают в таблицу:

Кроме того, пусть задана некоторая точка . Задача аппроксимации функции состоит в том, чтобы по имеющейся таблице найти число с известной степенью точности. Слово «аппроксимация» означает «приближение».

Легко понять, что если на функцию не накладываются никакие дополнительные условия, то постановка задачи бесперспективна. Мы будем далее предполагать, что функция обладает всеми производными. Оказывается, что в этом случае по имеющимся n+1 значениям можно найти еще одно и оценить, насколько оно точно.

Построим следующий многочлен:

Для ясности надо заметить, что в этой сумме - () слагаемых, что в слагаемом № k в числителе ровно множителей и что каждый из них является многочленом степени n. Этот многочлен называется многочленом Лагранжа таблицы значений функции.

Вот его основные свойства:

1. это - многочлен степени ;

2) , т.е. многочлен Лагранжа имеет в точках те же значения, что

и функция ;

3) если фиксировать любое число то окажется выполненным неравенство

где на участке , т.е. число ограничивает производную го порядка функции .

Сказанное означает, что если функция задана своей таблицей и требуется найти значение где-то в промежуточной точке c, то можно по таблице построить многочлен Лагранжа и его значение в этой точке принять за значение функции; ошибка, которая при этом возникнет, может быть оценена с помощью формулы, написанной выше в п.3).

Отыскание промежуточного значения функции называется интерполяцией; когда это делается с помощью многочлена Лагранжа, то говорят об интерпорляционном многочлене Лагранжа или об интерполяции по Лагранжу.

Замечание. Можно доказать, что существует один и только один многочлен степени n, который в заданных n+1 точках принимает заданные значения. Поэтому многочлен Лагранжа - это всего лишь одна из форм записи того самого единственного многочлена степени n, который определяется таблицей.

13,18. Метод простых итераций

Будем использовать обозначения предыдущей лекции. В частности, мы будем рассматривать систему линейных алгебраических уравнений, которую можно записывать и в матричном виде:

.

Напомним, что здесь А - матрица системы, B - столбец свободных членов, а X -столбец неизвестных. В предыдущей лекции речь шла о таком решении системы (3.1.1), которое с математической точки зрения является точным. В действительности ни один компьютер не манипулирует с точными числами - там числа приближенные; поэтому и при методе Гаусса, и при методе Крамера, и при методе жордановых исключений в действительности компьютер выдаст не точный, а приближенный ответ, хотя у самих этих методов «погрешность метода» равна нулю.

Существуют, однако, методы решения системы (3.1.1), которые по самой своей природе дают не точный, а приближенный ответ. Самым известным из таких методов является метод простых итераций. Вот его описание.

Преобразуем систему (3.1.1) к другому виду, выражая все неизвестные через самих себя,-

где - новые числовые матрицы, а Х - прежний столбец неизвестных. Переход от (3.1.1) к (3.1.2) можно сделать многими способами. Вот пример:

имеется система

;

из первого уравнения получим из второго уравнения следовательно, при таком преобразовании

Пусть столбцу неизвестных Х произвольным образом приписано конкретное числовое значение Тогда возникает возможность с помощью матричного равенства (3.1.2) построить реку-рентно столбцы , где k=2,3,4,... . Оказывается, что при некоторых условиях на D столбцы «приближаются как угодно близко» к решению системы (3.1.1). Действие по

вычислению с помощью называется итерацией; отсюда – метод итераций.

Введем новые термины для точного выражения последнего утверждения.

Пусть - столбец из n чисел, записанный ради экономии места в виде строки, заданный для каждого k=1,2,3,... . Пусть, далее, имеется столбец Назовем расстоянием от до число

ясно, что - числовая последовательность; если эта числовая последова-тельность стремится к нулю, то говорят, что столбцы стремятся к столбцу Z или что Z является пределом последовательности .

Таким образом, метод итераций решения системы линейных алгебраических уравнений состоит в построении последовательности , имеющей своим пределом столбец-решение.

Основное в организации процесса итераций - создать такую матрицу D, чтобы последо-вательность столбцов сходилась к решению. Сформулируем два условия, при выполнении лю-бого из которых процесс итераций сходится:

(1) если , то процесс итераций сходится к решению системы (3.1.1);

(2) если , то процесс итераций сходится к решению системы (3.1.1).

8. Разностные методы решения задачи Коши для ОДУ. Метод Эйлера.

Предположим, что порядок уравнения (6.3.1) равен 1 и, более того, его можно представить виде

(6.4.1) .

В случае первого порядка начальные условия превращаются в единственное равенство:

.

Искомая функция при численном подходе к проблеме решения всегда воспринимается через какую-то таблицу своих значений; иными словами, по заданным значениям аргумента надо найти такие , чтобы таблица

оказалась таблицей значений искомой функции. Для этого, в свою очередь, достаточно по заданному значению уметь находить значение в любой точке . Вот метод Эйлера для этого последнего поиска:

1й шаг. Фиксируем точность, с которой нужно найти значение . Обозначим это число через . Поясним, что это означает, что числа, отличающиеся меньше, чем на , считаются одинаковыми.

2й шаг. Фиксируем произвольное и разделим отрезок на равных частей: , где .

3й шаг. Построим последовательность чисел

,

в которой, напомним, . Обозначим через .

4й шаг. Заменим на и повторим шаги 2 и 3. Полученное число (т.е. последнее из вычисляемых на шаге 3) обозначим теперь через .

5й шаг. Если окажется, что числа и отличаются друг от друга меньше, чем на , то число считается найденным и равным . В противном случае переобо-значим через и вернемся к шагу 4.

Можно доказать, что когда функция из (7.4.1) имеет непрерывные частные производные, описанный процесс обязательно конечен и ответ находится действительно с любой наперед заданной точностью.

5. Интерполяция и приближение функций.

Пусть на отрезке [a,b] некоторая функция f(x) задана лишь в некоторых точках , т.е. известны ее значения , которые, как правило, собирают в таблицу:

Кроме того, пусть задана некоторая точка . Задача аппроксимации функции состоит в том, чтобы по имеющейся таблице найти число с известной степенью точности. Слово «аппроксимация» означает «приближение».

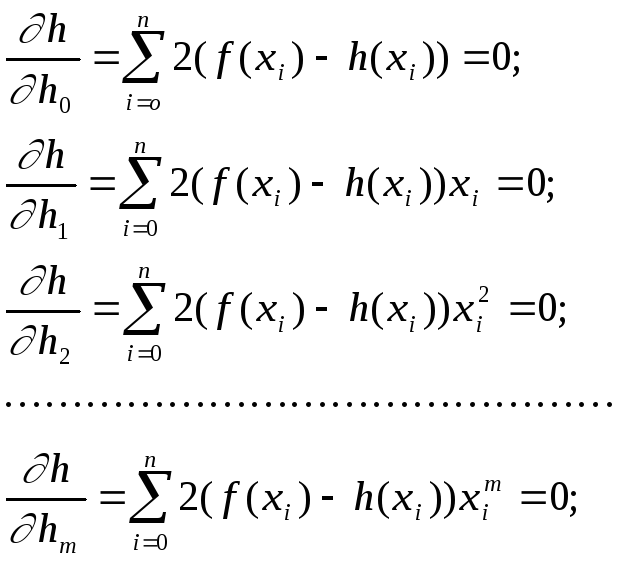
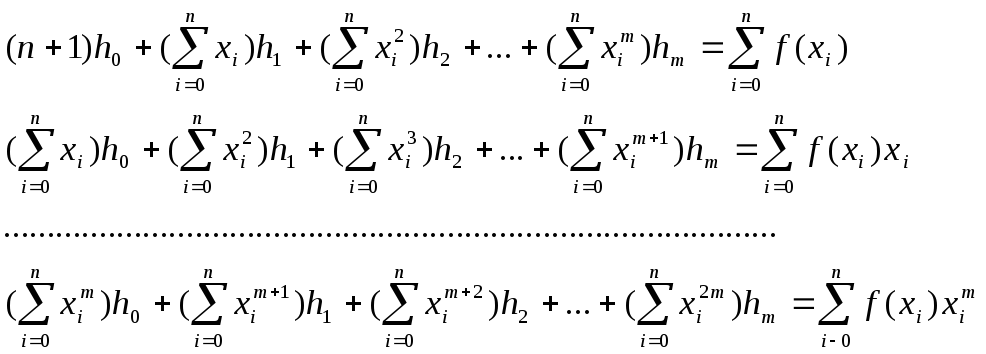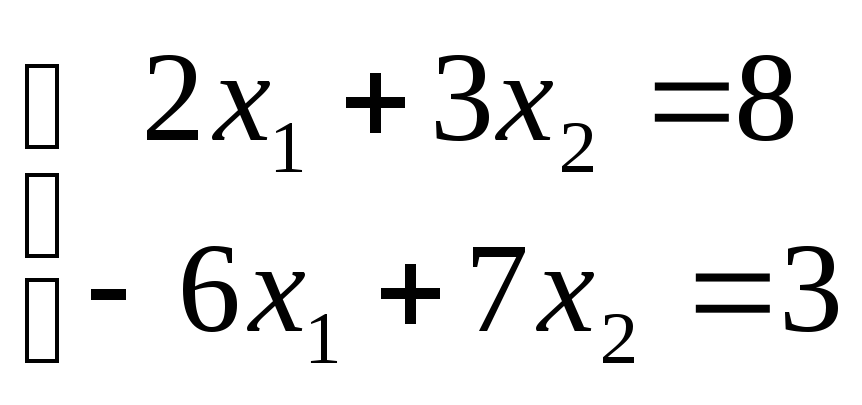Легко понять, что если на функцию не накладываются никакие дополнительные условия, то постановка задачи бесперспективна. Мы будем далее предполагать, что функция обладает всеми производными. Оказывается, что в этом случае по имеющимся n+1 значениям можно найти еще одно и оценить, насколько оно точно.