|
20.
Разностные методы решения задачи Коши
для ОДУ. Метод Рунге-Кутта.
В
той же ситуации, что и выше, т.е. при
поиске числа
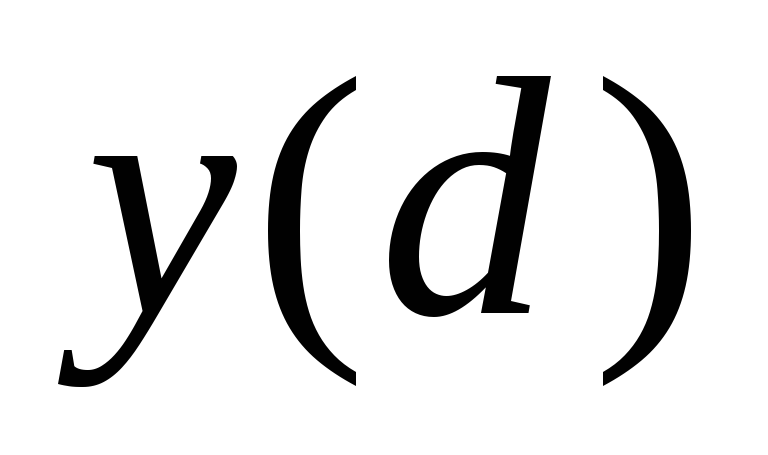 по числу
по числу
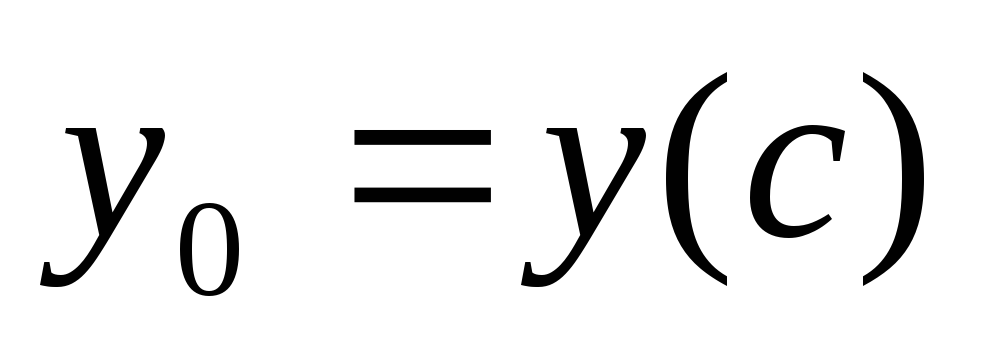 и равенству (6.4.1), существует еще один
широко применяемый метод - метод
Рунге-Кутта, который, как правило,
быстрее приводит к числу
и равенству (6.4.1), существует еще один
широко применяемый метод - метод
Рунге-Кутта, который, как правило,
быстрее приводит к числу
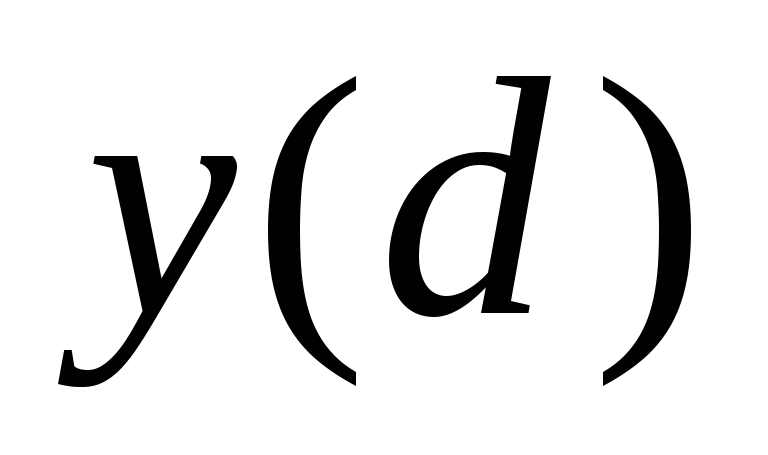 ,
чем метод Эйлера. Сформулируем действия
по методу Рунге-Кутта: ,
чем метод Эйлера. Сформулируем действия
по методу Рунге-Кутта:
1й
шаг.
Фиксируем точность, с которой нужно
найти значение
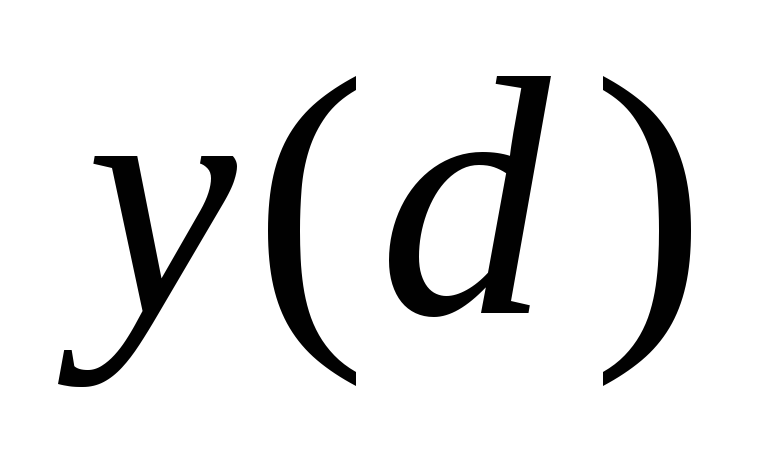 .
Обозначим это число через .
Обозначим это число через
 .
Поясним, что это означает, что числа,
отличающиеся меньше, чем на .
Поясним, что это означает, что числа,
отличающиеся меньше, чем на
 ,
считаются одинаковыми. ,
считаются одинаковыми.
2й
шаг.
Фиксируем произвольное
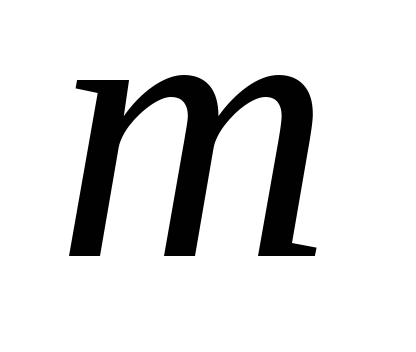 и разделим отрезок
и разделим отрезок
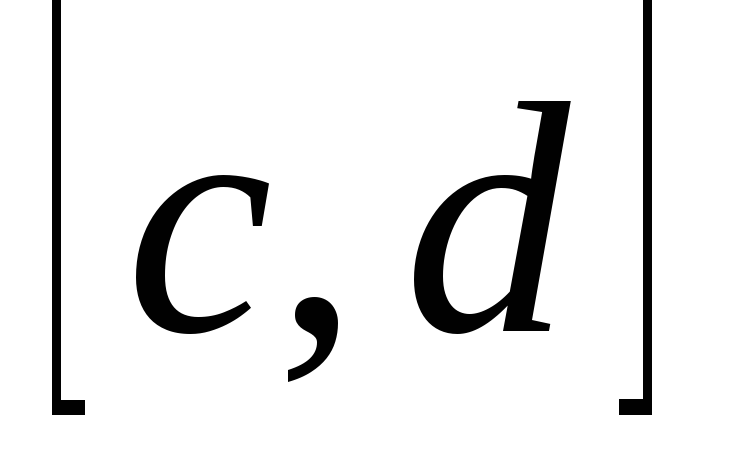 на
на
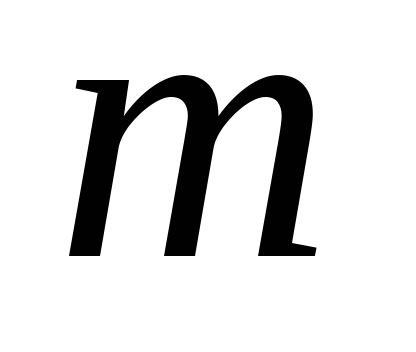 равных частей:
равных частей:
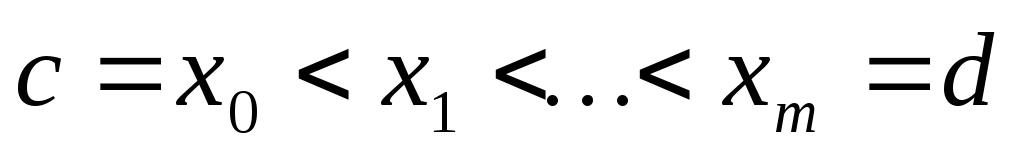 ,
где ,
где
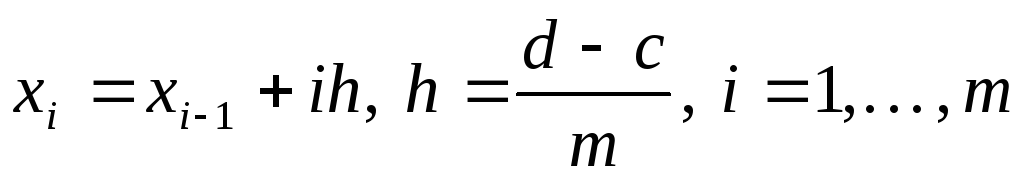 . .
3й
шаг.
Построим последовательность чисел
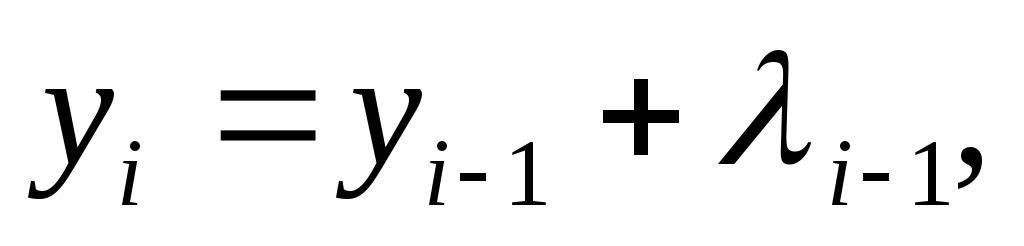 ,
где ,
где
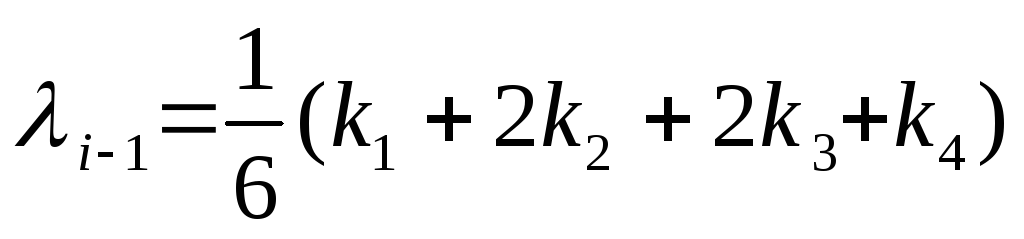 и
и

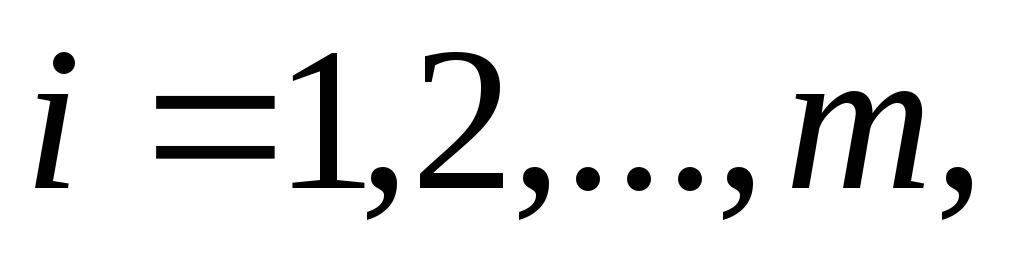
в
которой, напомним,
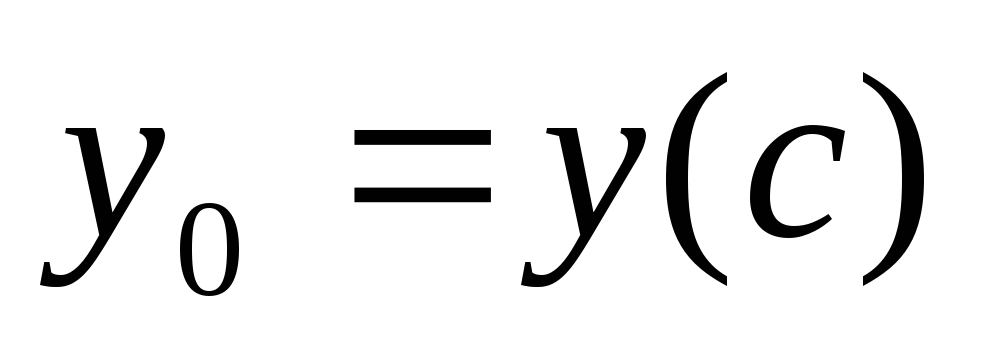 .
Обозначим .
Обозначим
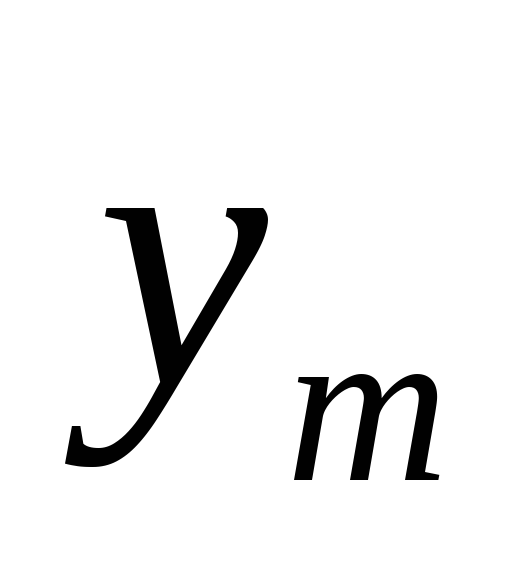 через
через
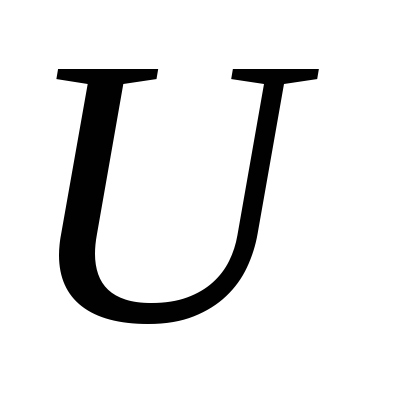 . .
4й
шаг.
Заменим
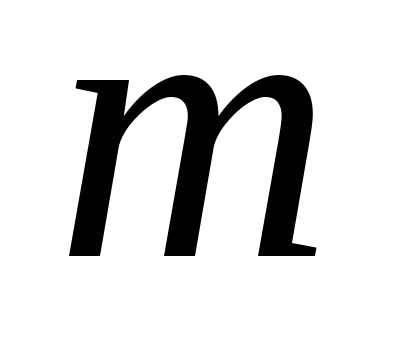 на
на
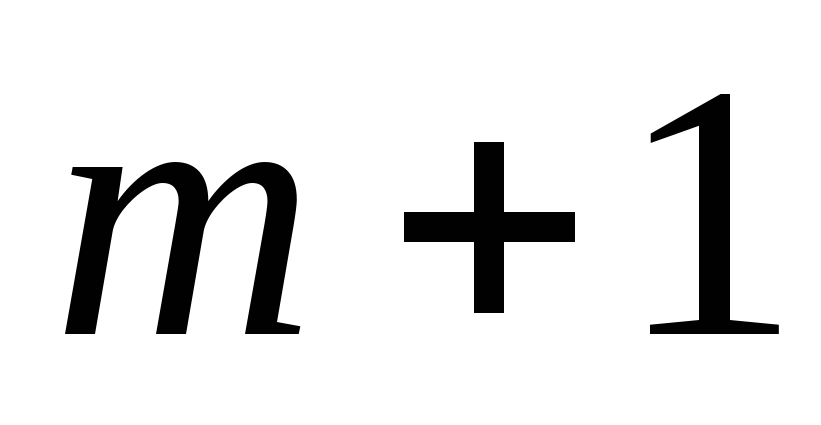 и повторим шаги 2 и 3. Полученное число
и повторим шаги 2 и 3. Полученное число
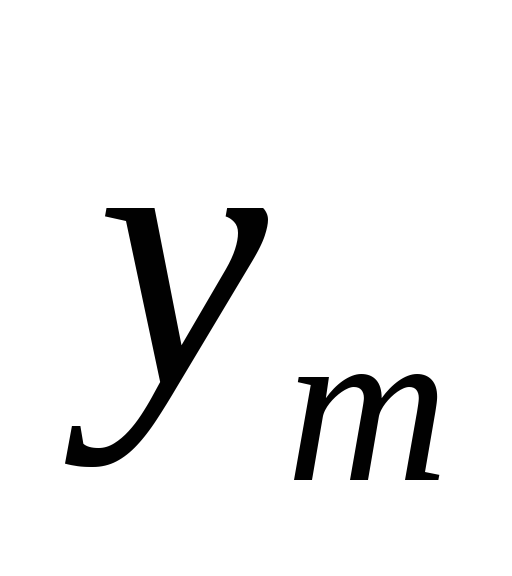 (т.е. послед-нее из вычисляемых на шаге
3) обозначим теперь через
(т.е. послед-нее из вычисляемых на шаге
3) обозначим теперь через
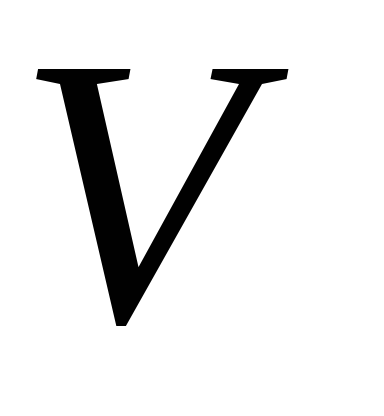 . .
5й
шаг.
Если окажется, что числа
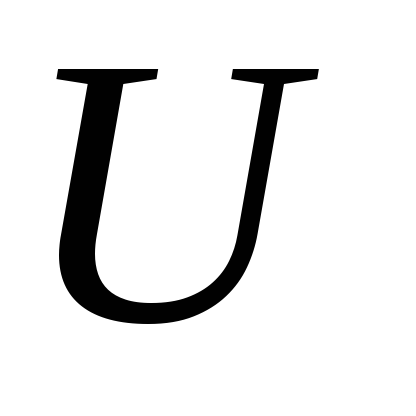 и
и
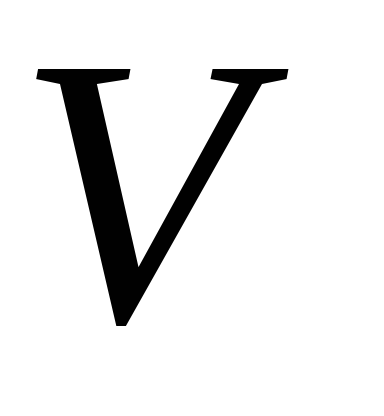 отличаются друг от друга меньше, чем
на
отличаются друг от друга меньше, чем
на
 ,
то число ,
то число
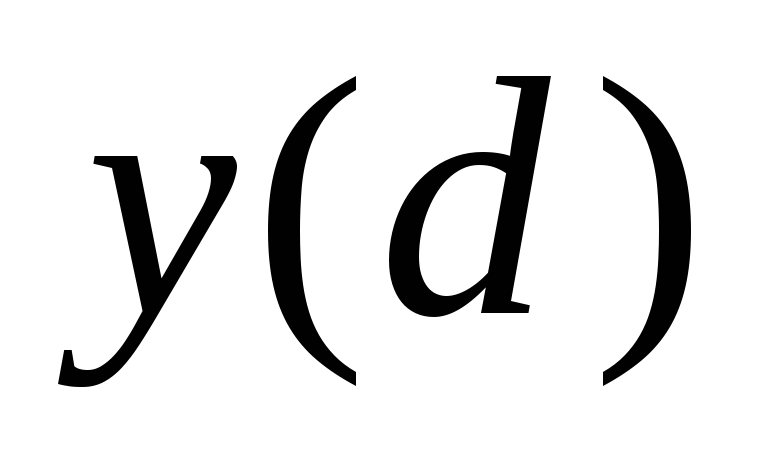 считается найденным и равным
считается найденным и равным
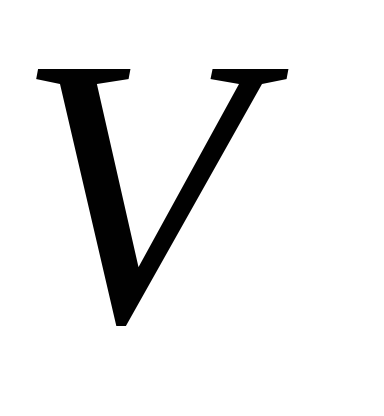 .
В противном случае переобозначим .
В противном случае переобозначим
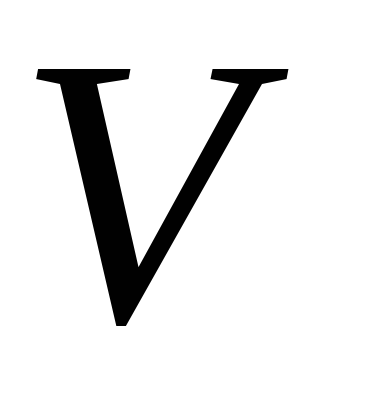 через
через
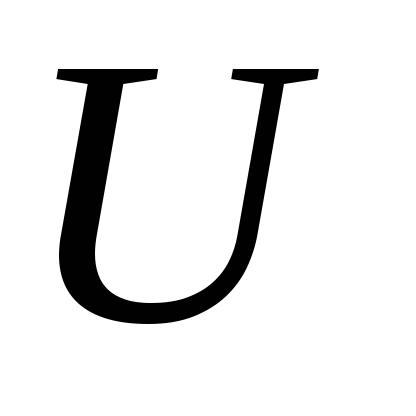 и вернемся к шагу 4.
и вернемся к шагу 4.
Можно
доказать, что когда
функция
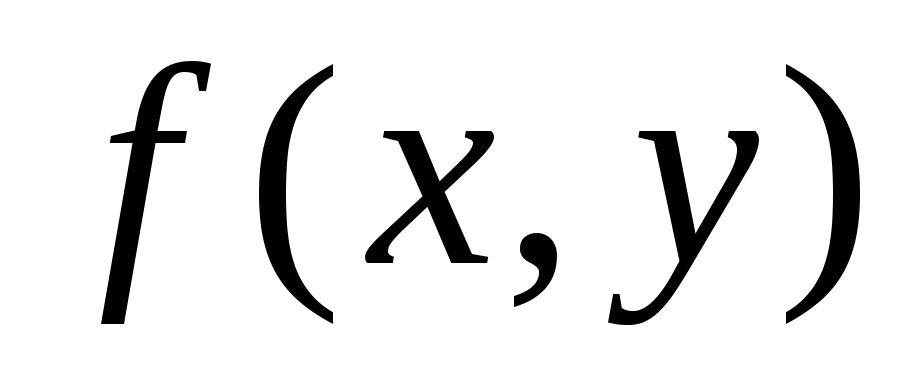 из
(7.4.1) имеет
непрерывные частные производные,
описанный процесс обязательно конечен
и ответ находится действительно с
любой наперед заданной точностью.
из
(7.4.1) имеет
непрерывные частные производные,
описанный процесс обязательно конечен
и ответ находится действительно с
любой наперед заданной точностью.
|
13.
Приближенные методы решения нелинейных
уравнений. Метод Дихатоми.
Предположим,
что имеется система уравнений вида:
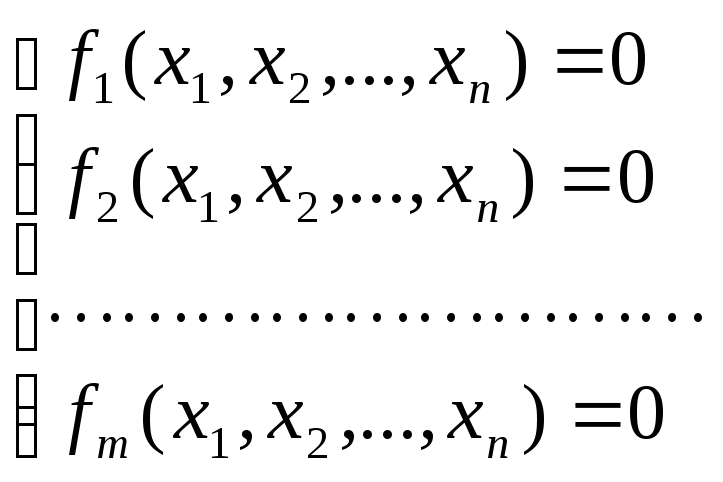 . .
Ее
решение - это любой набор чисел
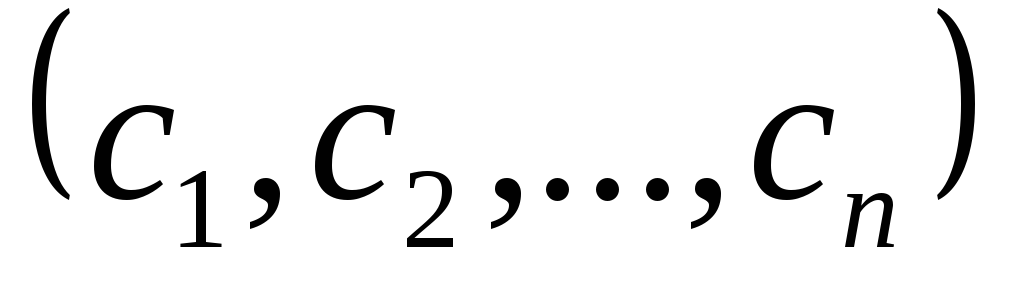 такой, что при подстановке в систему
ci
вместо xi
, i=1,2,...,n,
все равенства становятся тождествами
(т.е. получаются выражения типа «0=0»).
Решить систему - это значит найти все
решения.
такой, что при подстановке в систему
ci
вместо xi
, i=1,2,...,n,
все равенства становятся тождествами
(т.е. получаются выражения типа «0=0»).
Решить систему - это значит найти все
решения.
отделить
корень уравнения
(3.3.1) - это значит найти такой интервал
(a,b),
который, во-первых, содержит корень
уравнения (3.3.1) и, во-вторых, со-держит
только один корень этого уравнения.
Доказывается, что если
на концах некоторого интервала (a,b)
функция
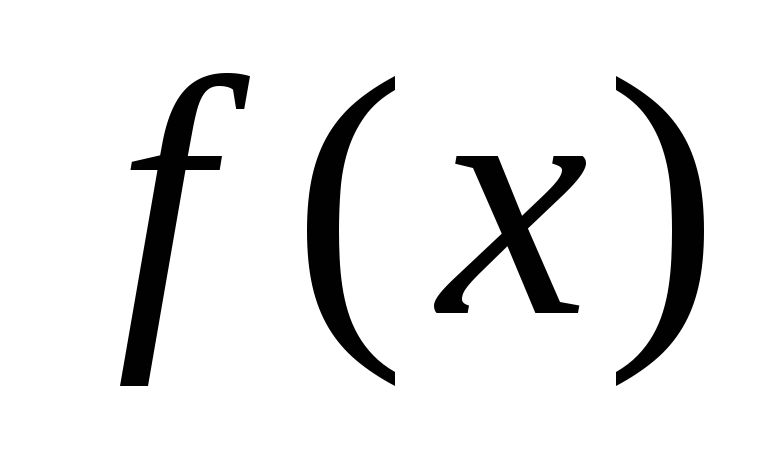 имеет разные знаки, а внутри этого
интервала производная
имеет разные знаки, а внутри этого
интервала производная
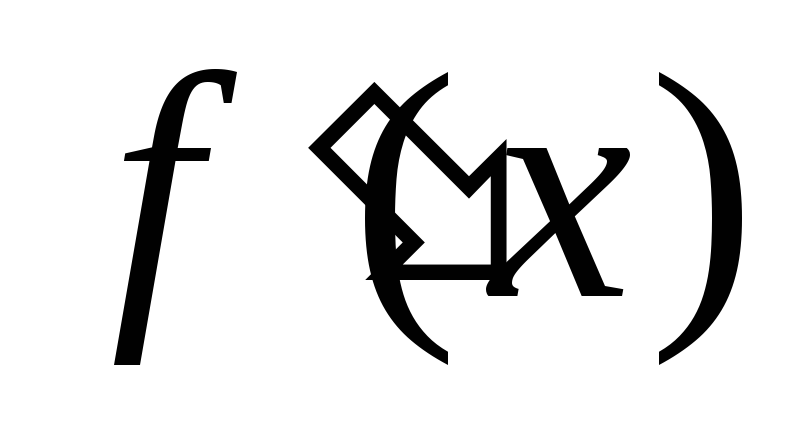 знак
не меняет, то в интервале (a,b) корень
уравнения (3.3.1)
есть и, притом, только один. знак
не меняет, то в интервале (a,b) корень
уравнения (3.3.1)
есть и, притом, только один.
Отсюда
возникает простая методика приближенного
поиска корня, отделенного в интервале
(a,b):
надо построить последовательность
точек
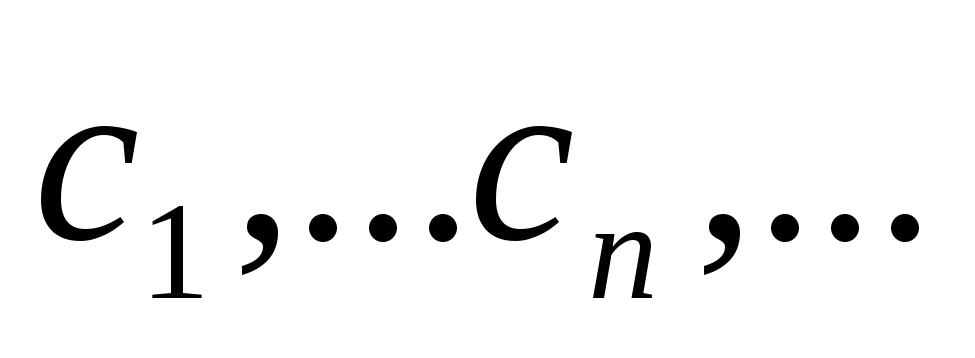 по
следующему правилу: по
следующему правилу:
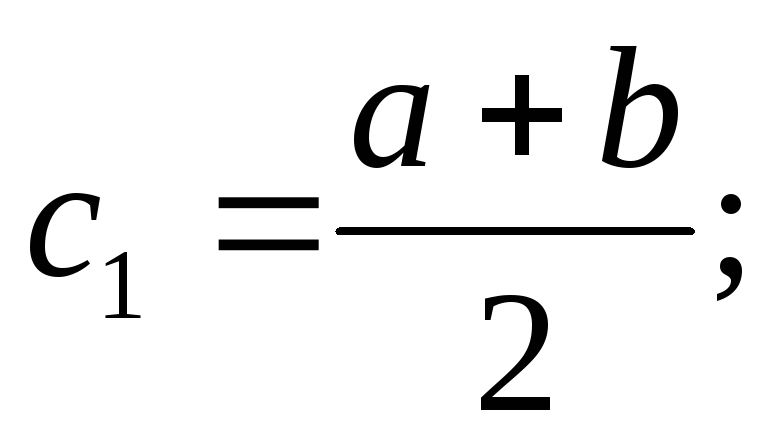 затем
из двух интервалов (a,c1)
и (c1,b)
выбирается тот, на концах которого затем
из двух интервалов (a,c1)
и (c1,b)
выбирается тот, на концах которого
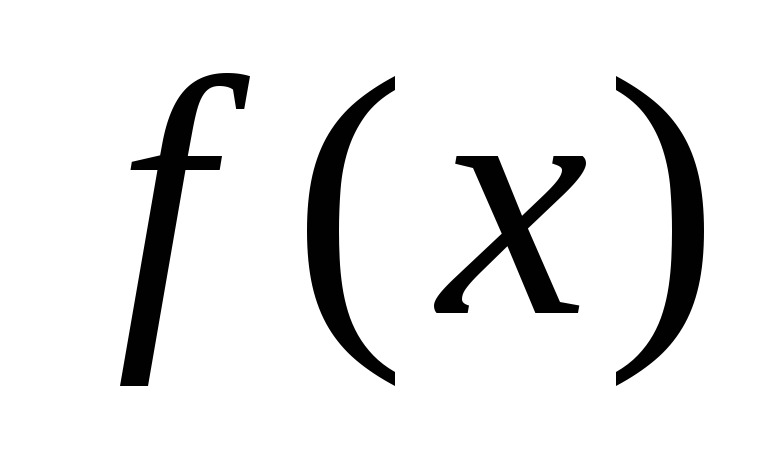 имеет разные знаки и его середина
принимается за
имеет разные знаки и его середина
принимается за
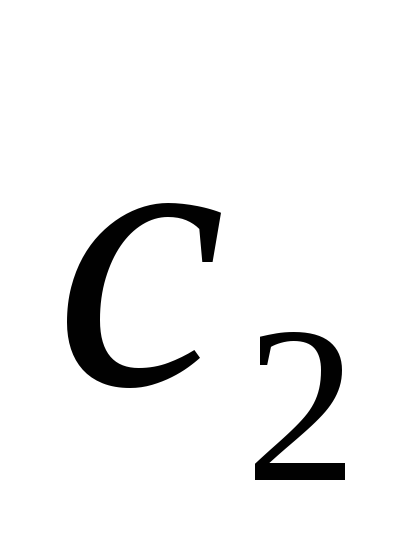 ;
обозначим кон-цы этого интервала (у
которого ;
обозначим кон-цы этого интервала (у
которого
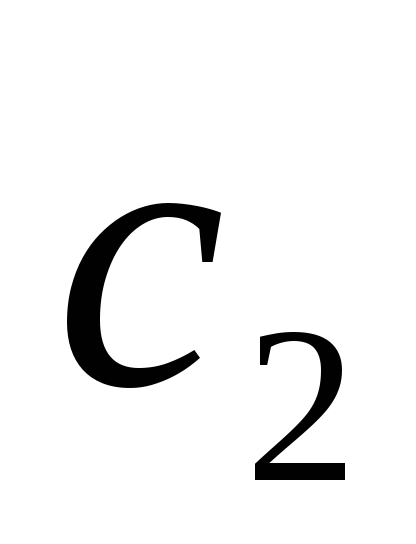 -
середина) через (a2,b2),
а затем выберем ту из его половин, на
концах которой -
середина) через (a2,b2),
а затем выберем ту из его половин, на
концах которой
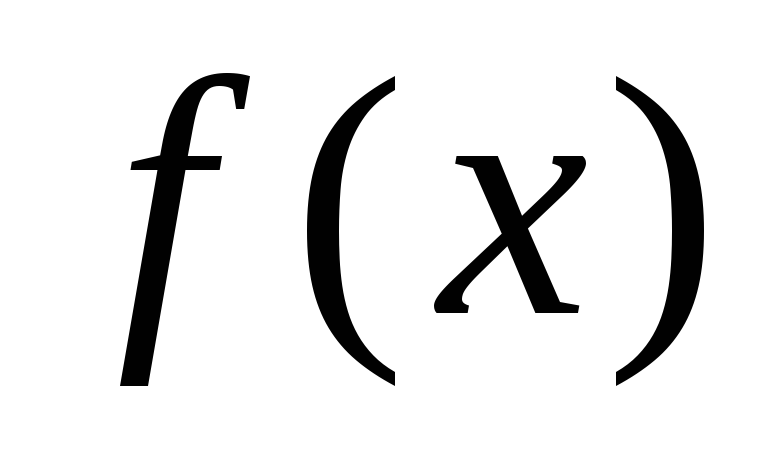 имеет
разные знаки. Пусть (a3,b3)
- эта половина и имеет
разные знаки. Пусть (a3,b3)
- эта половина и
 - середина этого отрезка и т.д.
Доказывается, что построенная
последовательность
- середина этого отрезка и т.д.
Доказывается, что построенная
последовательность
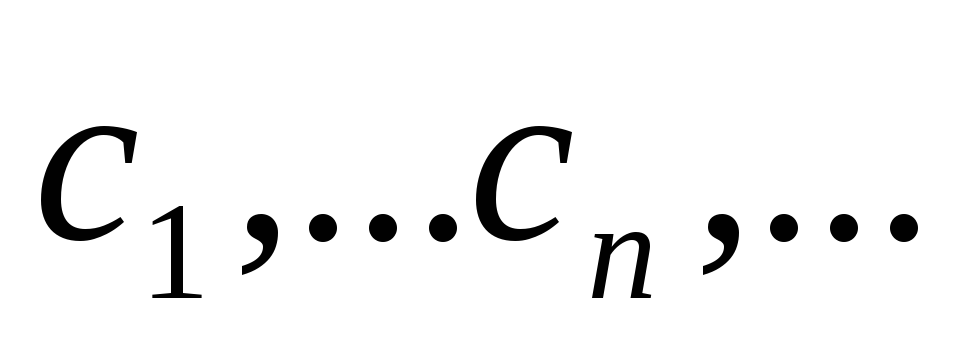 сходится к корню уравнения (3.3.1). Если
с самого начала задается некоторая
точность вычислений, то на практике
построение последовательности
сходится к корню уравнения (3.3.1). Если
с самого начала задается некоторая
точность вычислений, то на практике
построение последовательности
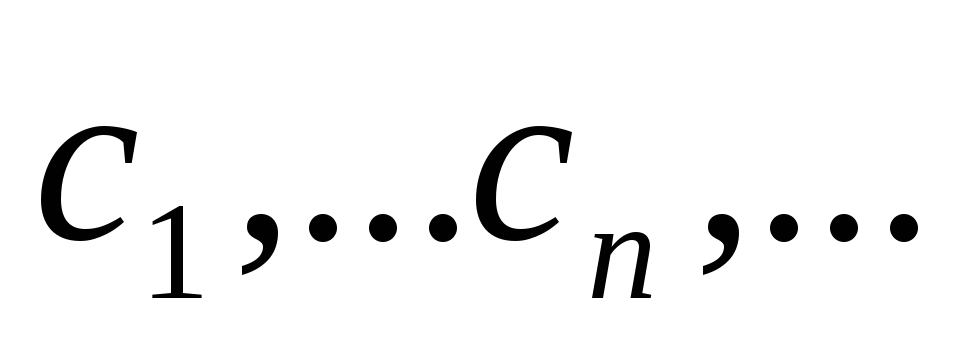 прерывается тогда, когда два раза
подряд получаются одинаковые с заданной
точностью числа. Это последнее перед
прерыванием построения последовательности
число и принимается за приближенное
с заданной степенью точности значение
корня.
прерывается тогда, когда два раза
подряд получаются одинаковые с заданной
точностью числа. Это последнее перед
прерыванием построения последовательности
число и принимается за приближенное
с заданной степенью точности значение
корня.
Описанный
метод уточнения корня называется
методом
деления отрезка пополам.
9.
Приближенные методы решения нелинейных
уравнений. Методы касательных и секущих
(хорд).
Предположим,
что имеется система уравнений вида:
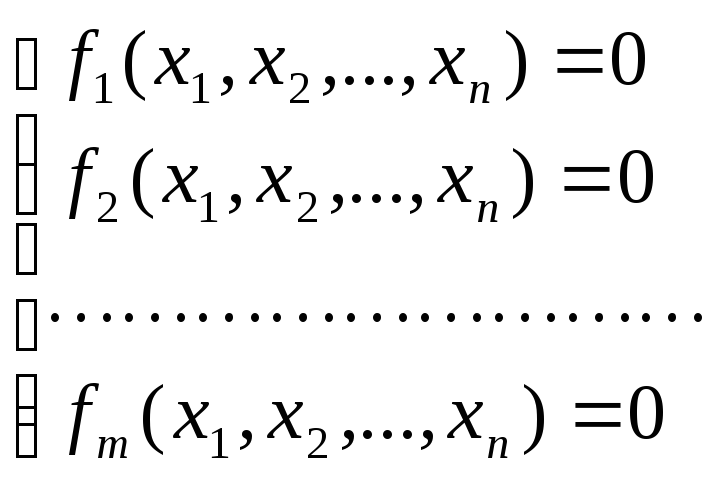 . .
Ее
решение - это любой набор чисел
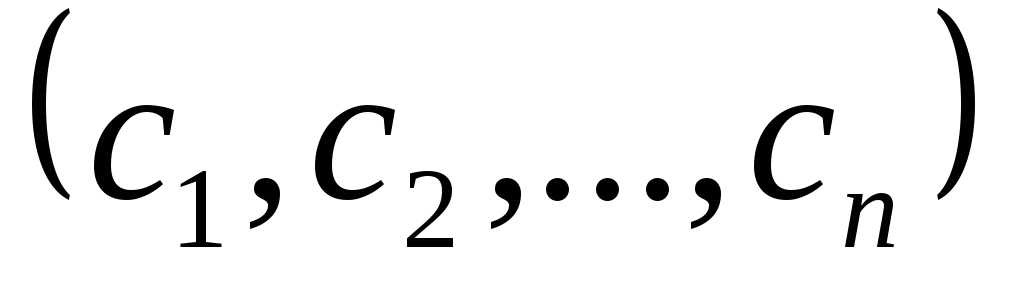 такой, что при подстановке в систему
ci
вместо xi
, i=1,2,...,n,
все равенства становятся тождествами
(т.е. получаются выражения типа «0=0»).
Решить систему - это значит найти все
решения.
такой, что при подстановке в систему
ci
вместо xi
, i=1,2,...,n,
все равенства становятся тождествами
(т.е. получаются выражения типа «0=0»).
Решить систему - это значит найти все
решения.
Метод
хорд
Предположим
теперь на отрезке
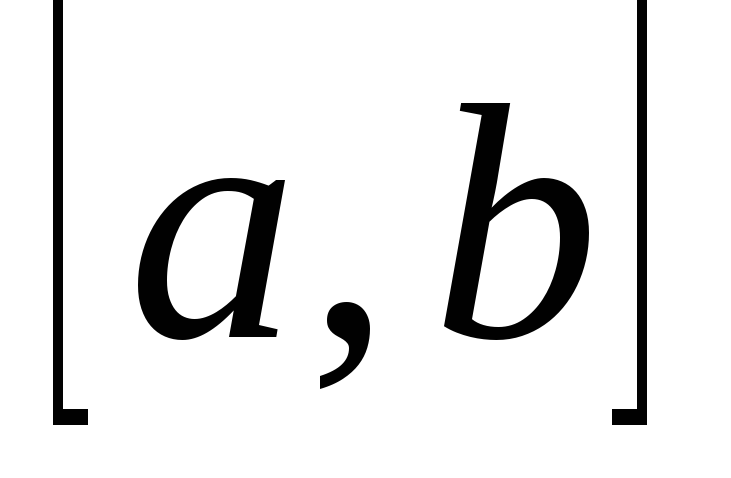 уже
отделен корень уравнения (3.3.1). В методе
хорд строится некоторая последовательность
отрезков
уже
отделен корень уравнения (3.3.1). В методе
хорд строится некоторая последовательность
отрезков
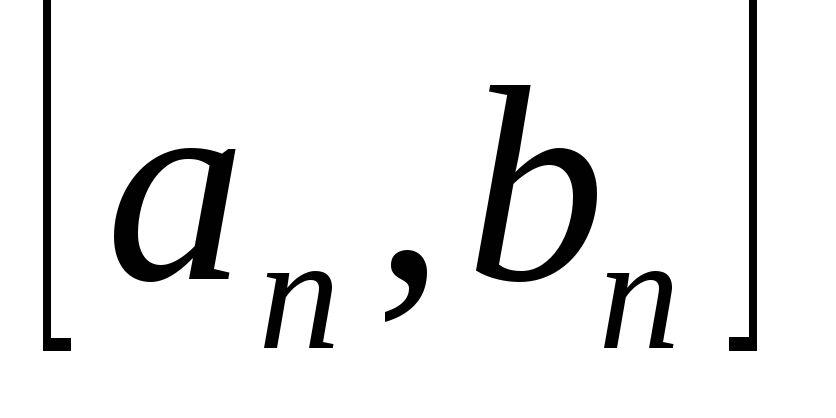 и точек
и точек
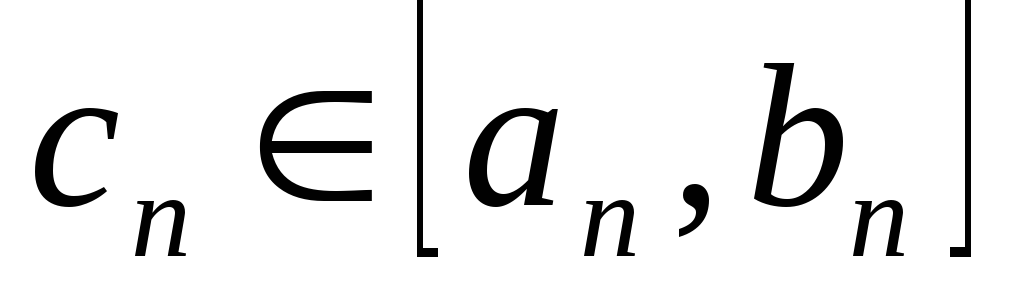 ,
сходящихся к корню. ,
сходящихся к корню.
В
качестве отрезка
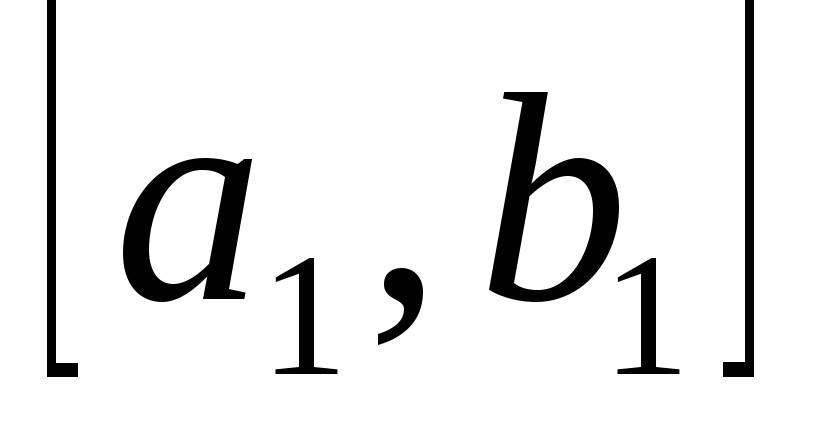 берется отрезок
берется отрезок
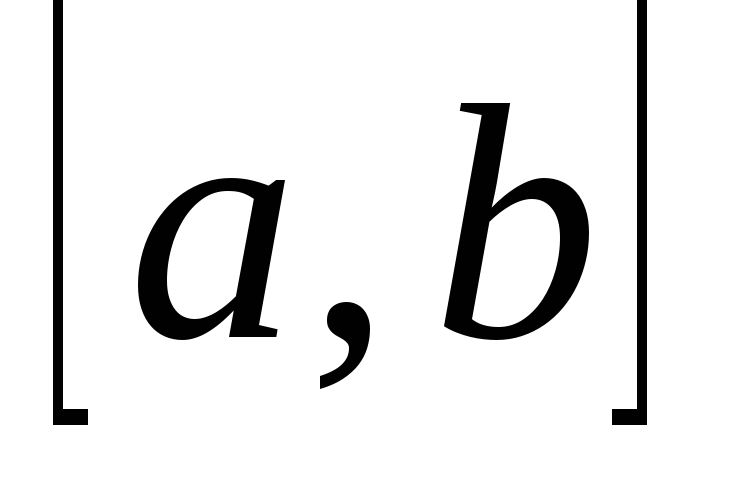 .
Точка с1
берется как точка пересечения с осью
абсцисс прямой, проходящей через точки .
Точка с1
берется как точка пересечения с осью
абсцисс прямой, проходящей через точки
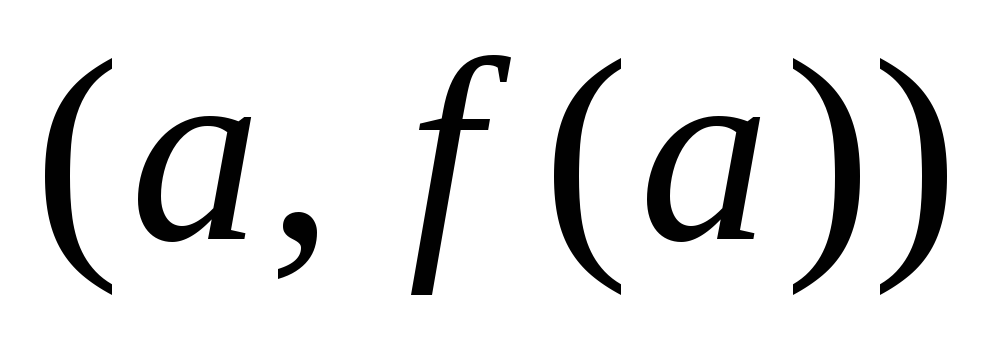 и
и
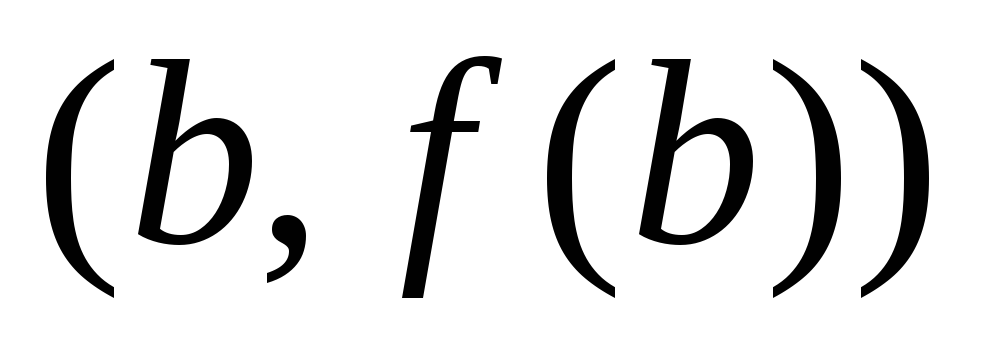 .
Укажем значение для c1
в явной форме: .
Укажем значение для c1
в явной форме:
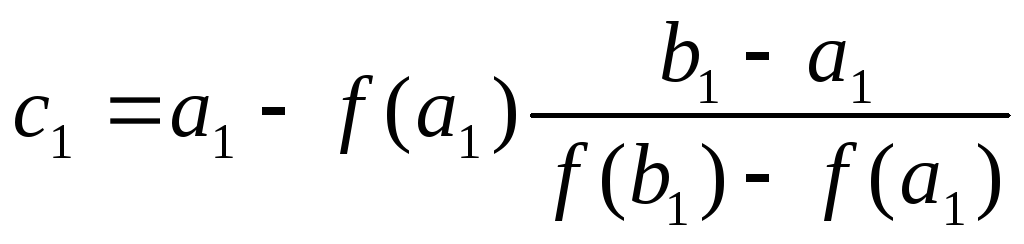 . .
Из
двух отрезков
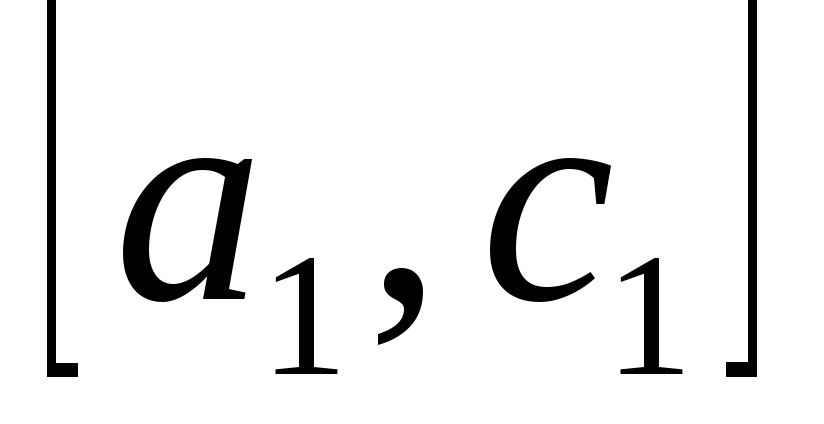 и
и
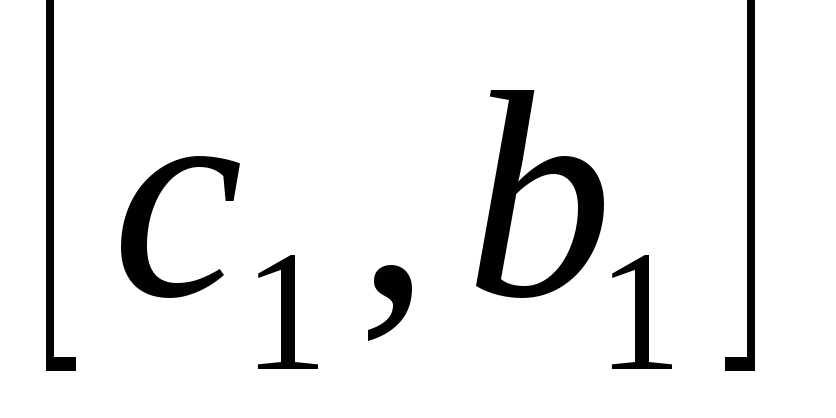 выберем
тот, на концах которого функция выберем
тот, на концах которого функция
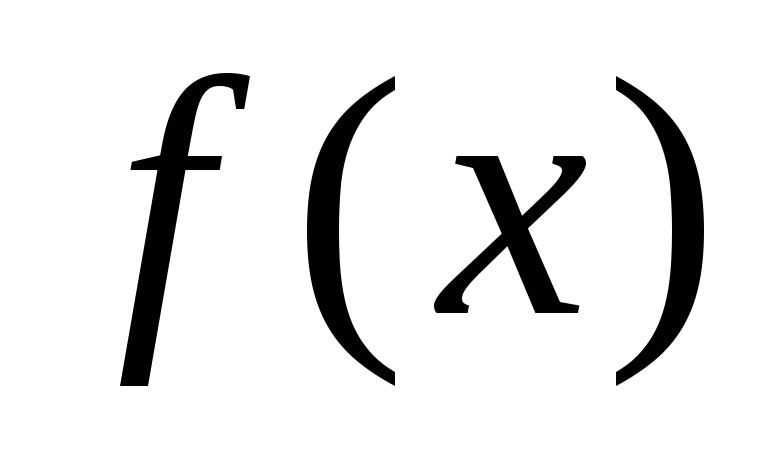 имеет
разные знаки и этот отрезок примем за
имеет
разные знаки и этот отрезок примем за
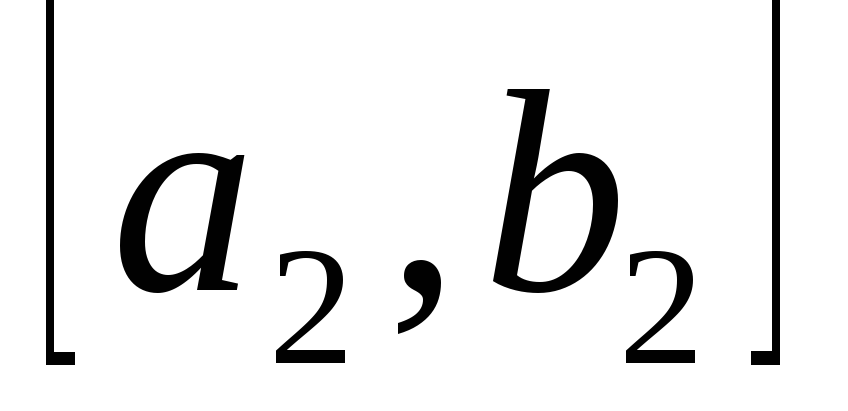 .
Затем найдем точку .
Затем найдем точку
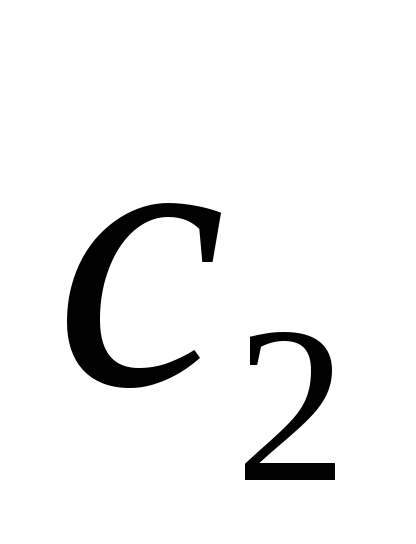 по
отрезку
по
отрезку
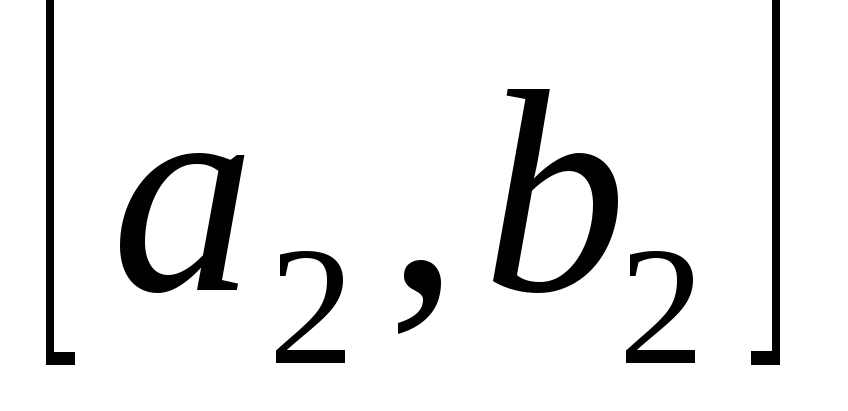 точно так же, как нашли точку
точно так же, как нашли точку
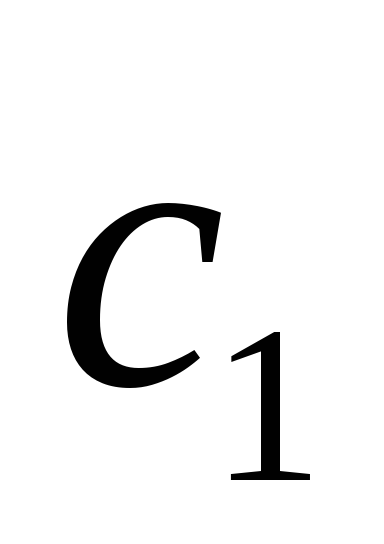 по отрезку
по отрезку
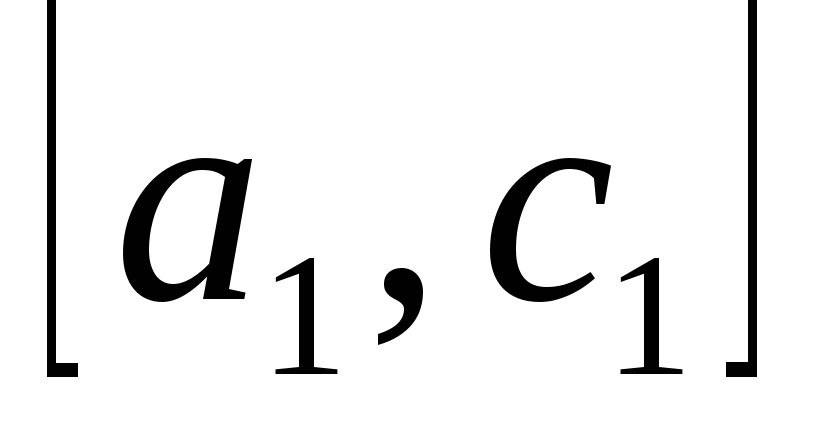 :
это будет точка пересечения с осью
абсцисс прямой, проходящей через точки :
это будет точка пересечения с осью
абсцисс прямой, проходящей через точки
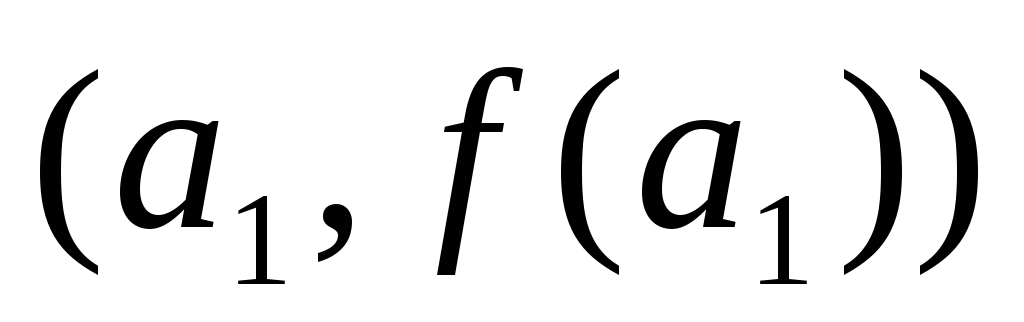 и
и
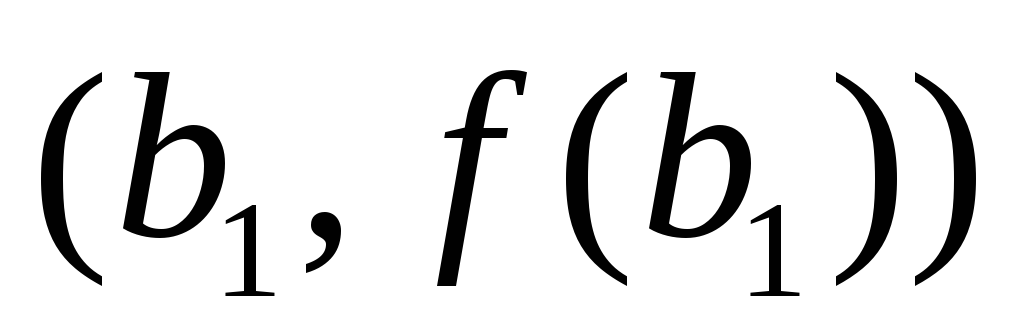 : :
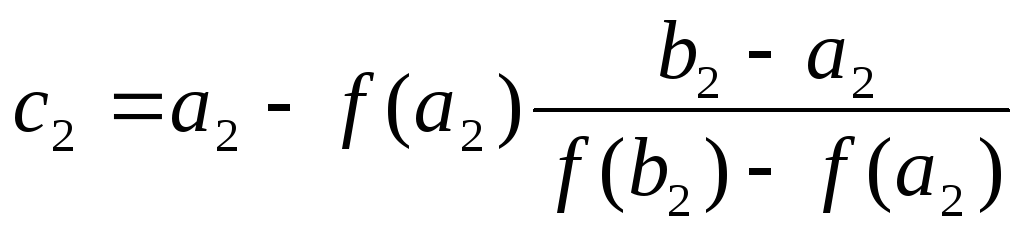 . .
Затем
в качестве отрезка
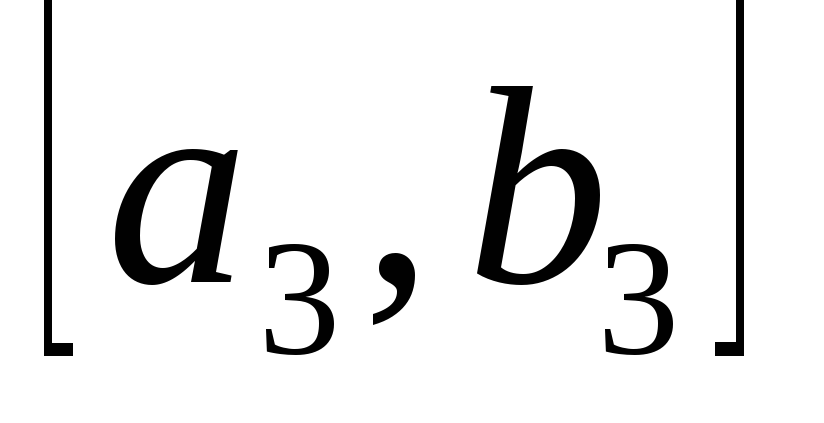 берется тот из отрезков
берется тот из отрезков
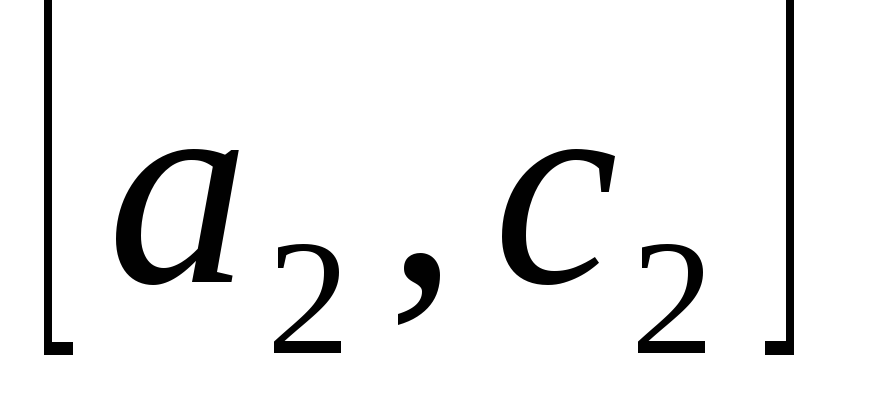 и и
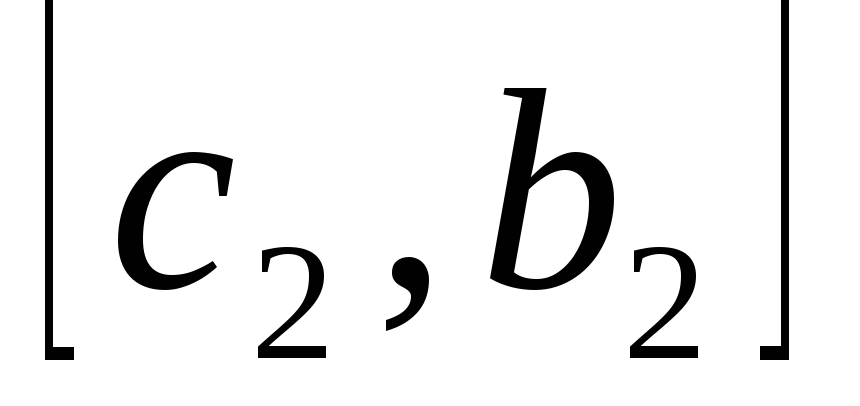 ,
на концах которого ,
на концах которого
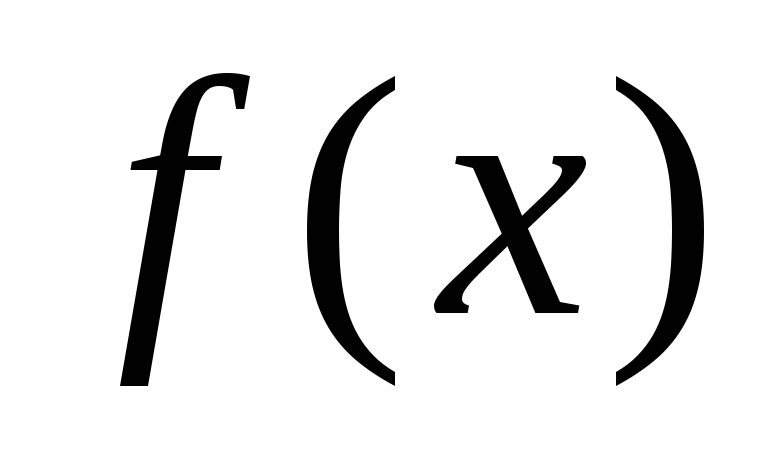 имеет
разные знаки и т.д. Через последовательность
точек имеет
разные знаки и т.д. Через последовательность
точек
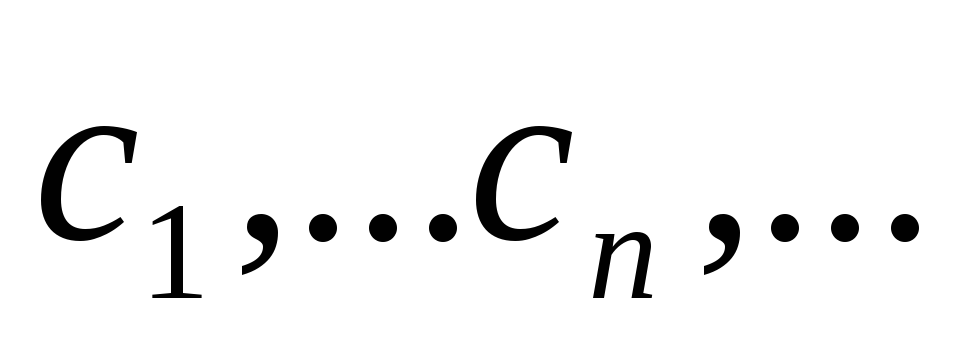 приближенное значение корня находится
так же, как в п.1.
Название метода происхо-дит из того,
что конструируемые по ходу дела прямые
являются хордами по отношению к графику
функции.
приближенное значение корня находится
так же, как в п.1.
Название метода происхо-дит из того,
что конструируемые по ходу дела прямые
являются хордами по отношению к графику
функции.
Метод
касательных Вновь
рассмотрим ситуацию отделенного на
отрезке
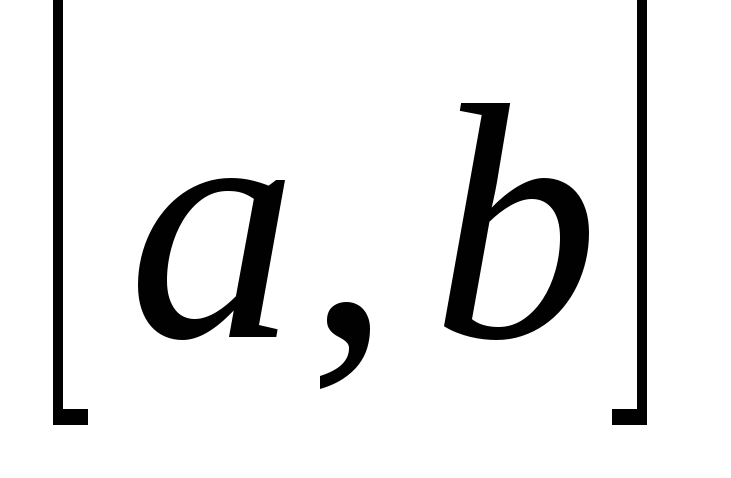 корня уравнения
корня уравнения
(3.3.1).
Будем предполагать, что функция
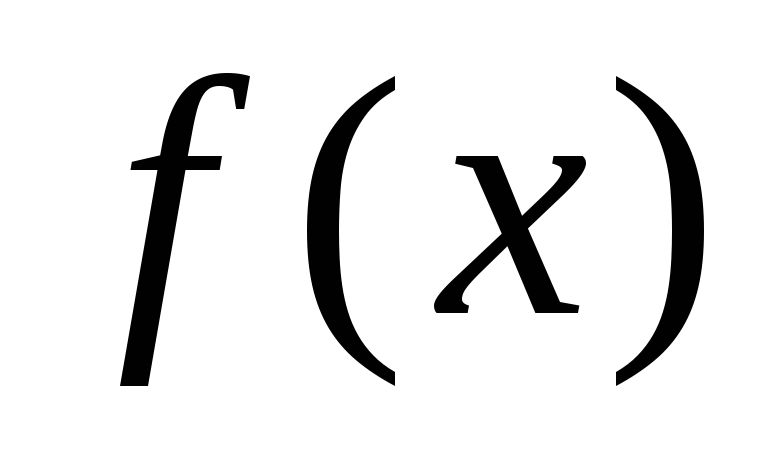 имеет
разные знаки на концах этого отрезка,
а ее первые две
производные на этом отрезке знака не
меняют. На нижеприведенной схеме
первая и вторая производные функции
имеет
разные знаки на концах этого отрезка,
а ее первые две
производные на этом отрезке знака не
меняют. На нижеприведенной схеме
первая и вторая производные функции
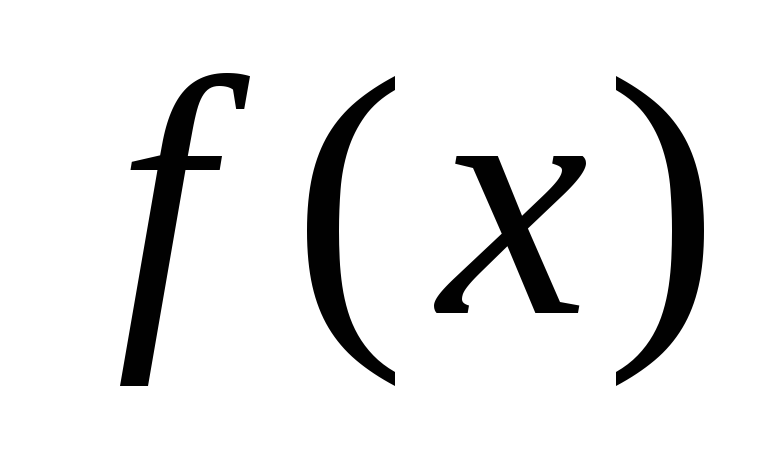 положительны.
В случае метода касательных уточнения
корня также строится последовательность
отрезков положительны.
В случае метода касательных уточнения
корня также строится последовательность
отрезков
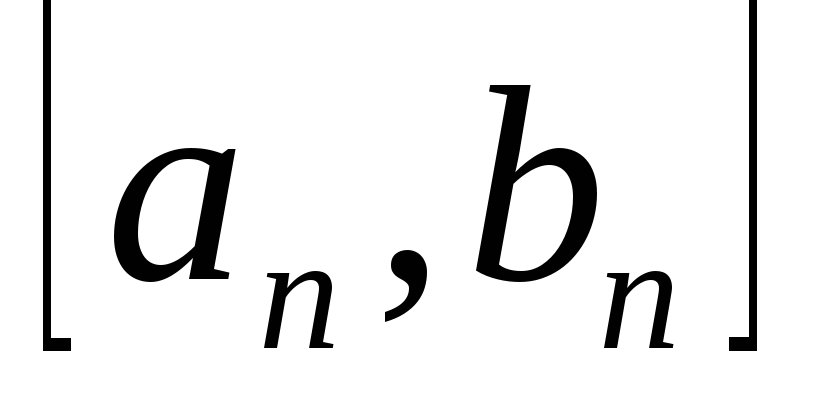 и точек
и точек
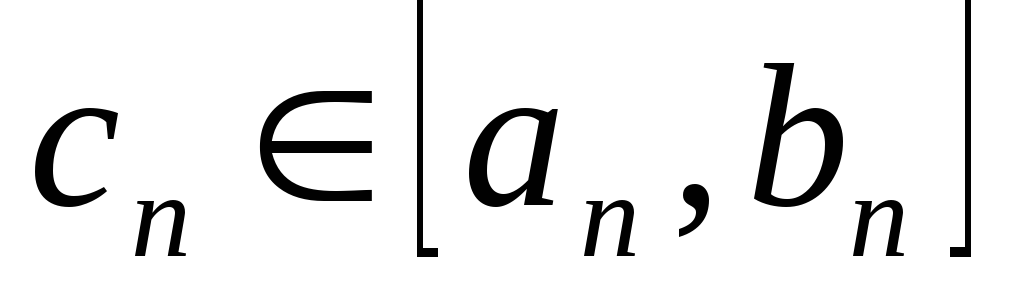 ,
сходящихся к корню. ,
сходящихся к корню.
Пусть
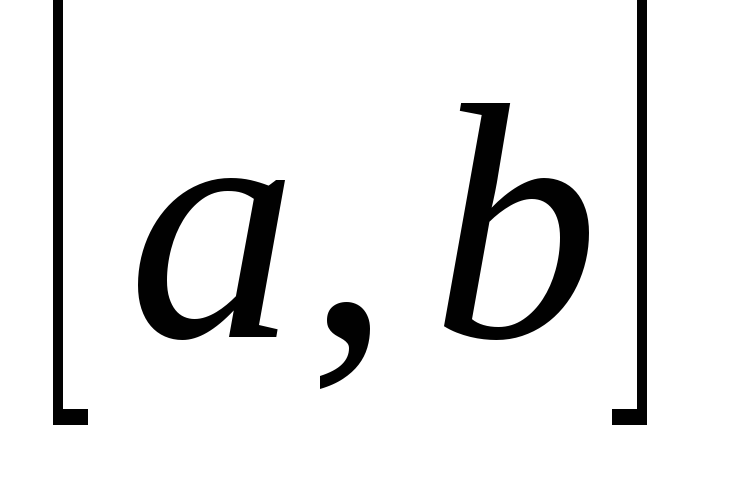 = =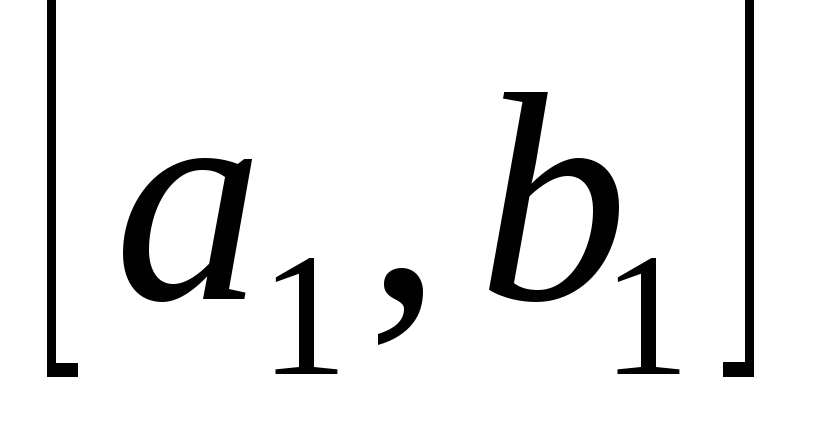 .
Выберем тот край отрезка .
Выберем тот край отрезка
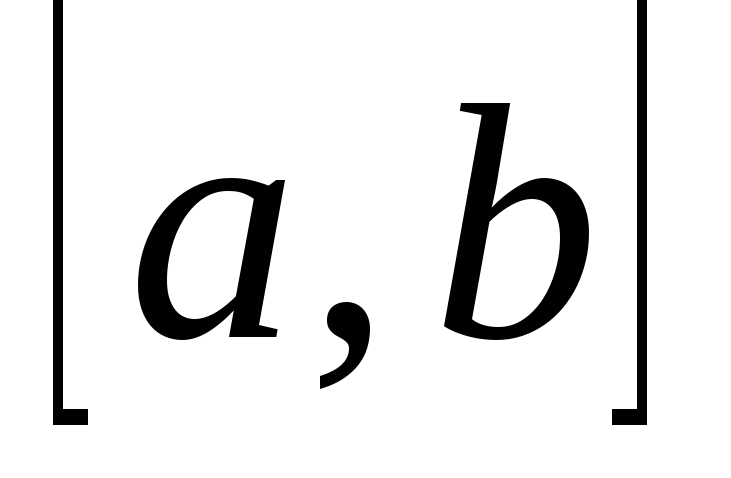 ,
на котором функция имеет тот же знак,
что и ее вторая производная. В нашем
примере на приведенной выше схеме -
это точка b.
Проведем через точку ,
на котором функция имеет тот же знак,
что и ее вторая производная. В нашем
примере на приведенной выше схеме -
это точка b.
Проведем через точку
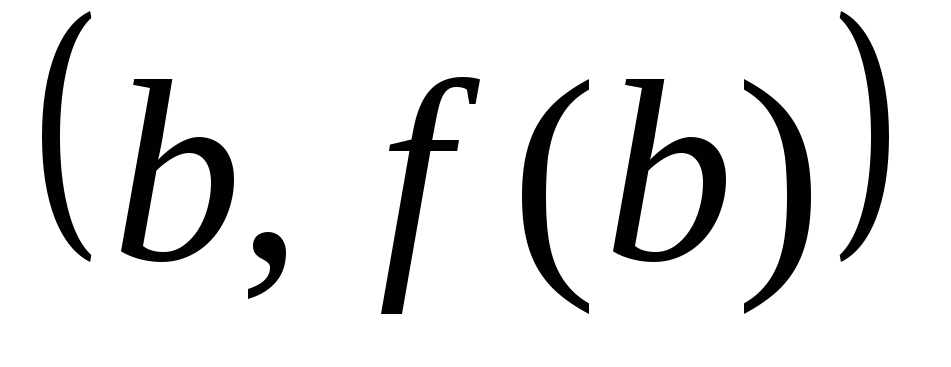 касательную
к графику функции касательную
к графику функции
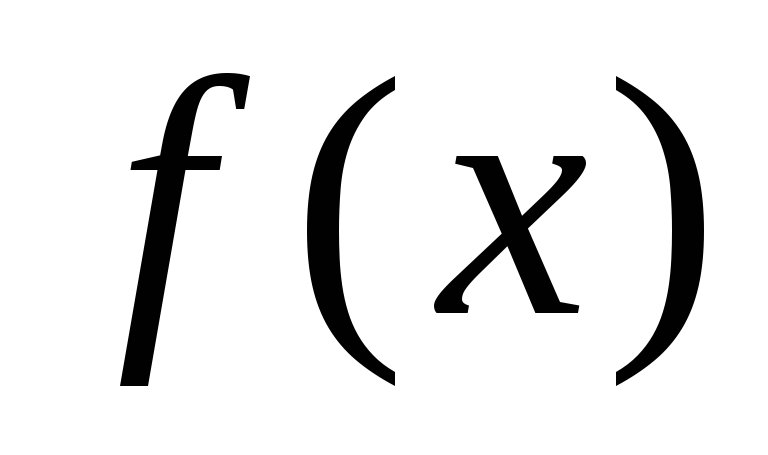 .
Точку пересечения этой касательной
с осью абсцисс и примем за точку c1.
Вот соответствующая формула для
рассматриваемого случая: .
Точку пересечения этой касательной
с осью абсцисс и примем за точку c1.
Вот соответствующая формула для
рассматриваемого случая:

Нетрудно
получить аналогичные формулы для
случаев, когда знаки упомянутых выше
значений иные. Важен принцип: касательная
проводится к графику в той точке, где
знак значения функции совпадает со
знаком ее второй производной. После
этого из двух отрезков
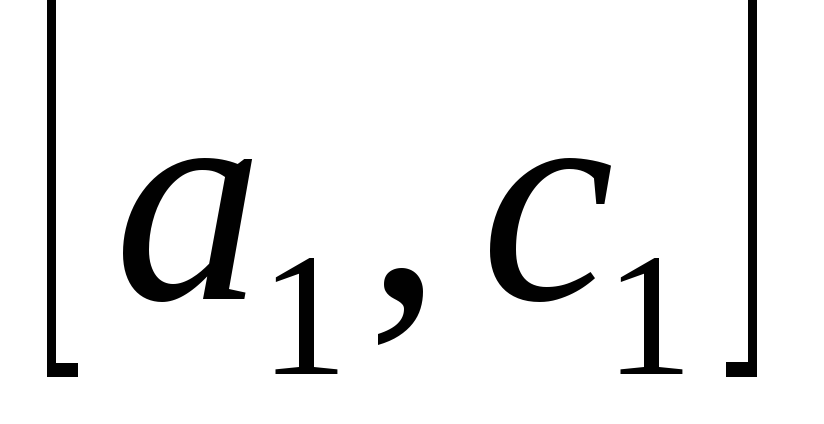 и
и
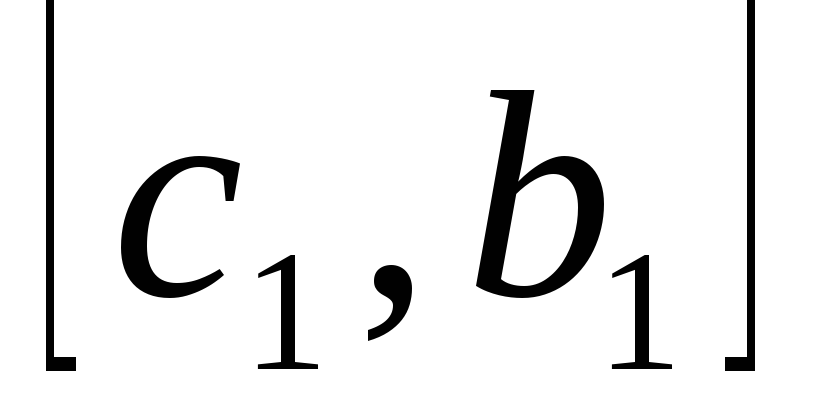 выберем
тот, на концах которого функция
выберем
тот, на концах которого функция
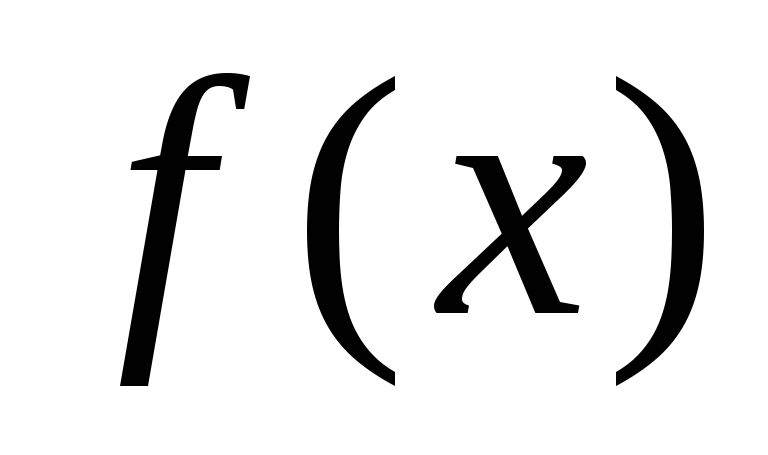 имеет
разные знаки и этот отрезок примем за имеет
разные знаки и этот отрезок примем за
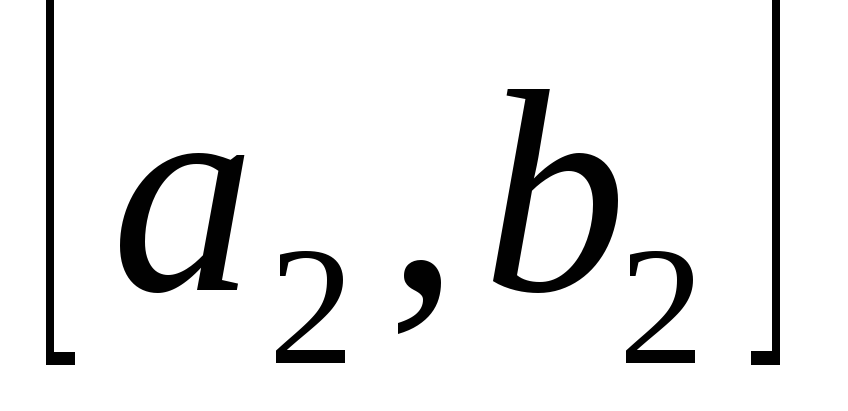 .
Затем найдем точку .
Затем найдем точку
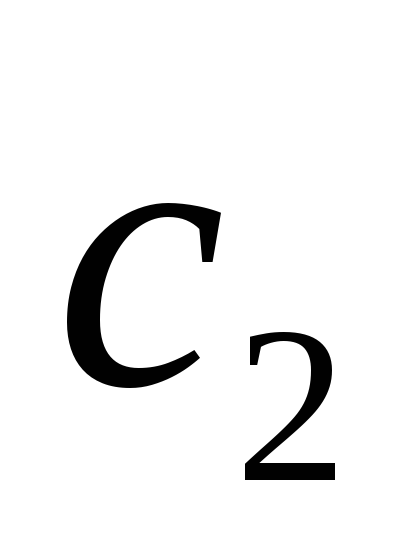 по отрезку
по отрезку
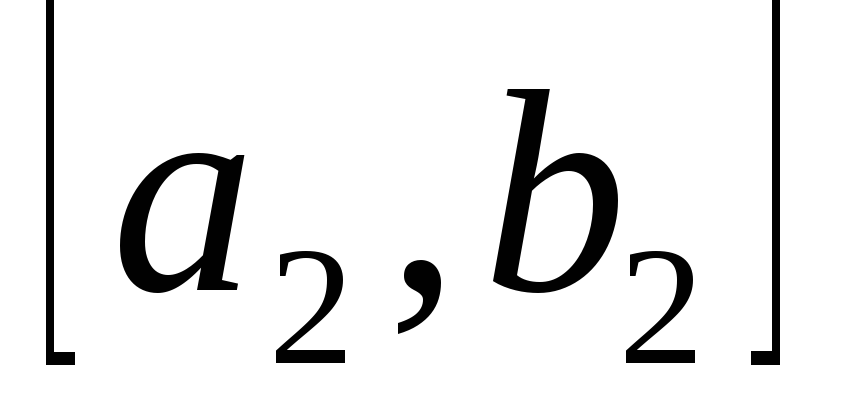 точно так же, как нашли точку
точно так же, как нашли точку
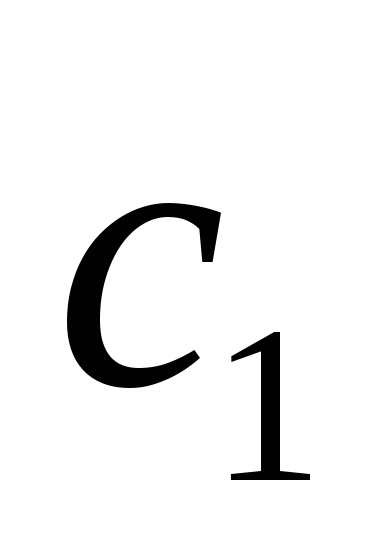 по отрезку
по отрезку
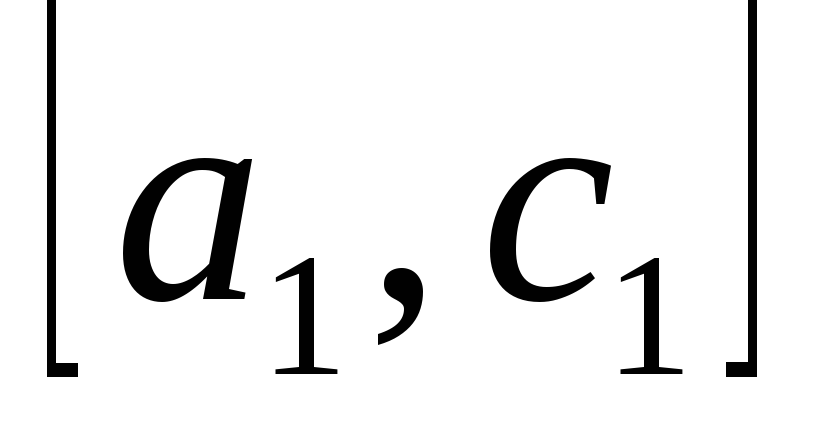 и
т.д. Через последовательность точек
и
т.д. Через последовательность точек
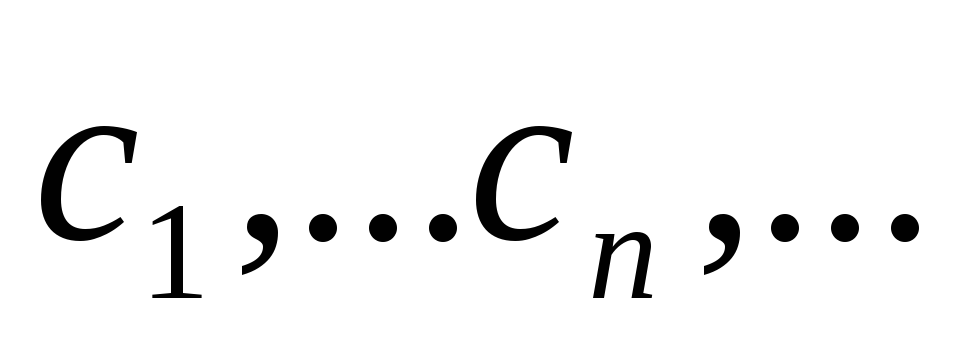 приближенное значение корня находится
так же, как в п.1.
приближенное значение корня находится
так же, как в п.1.
|



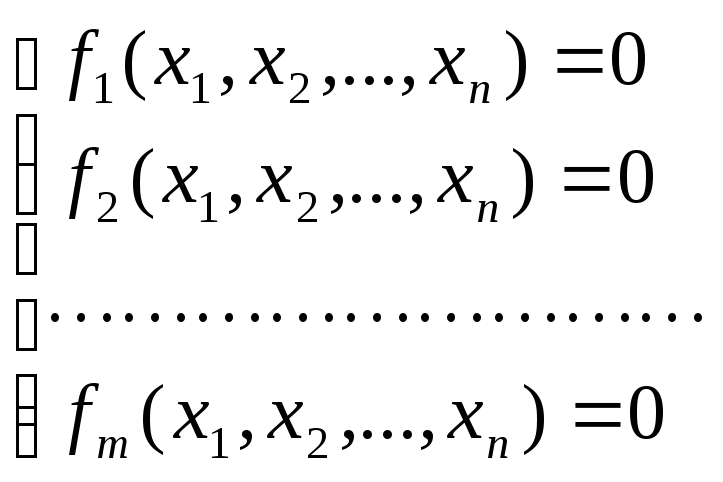 .
.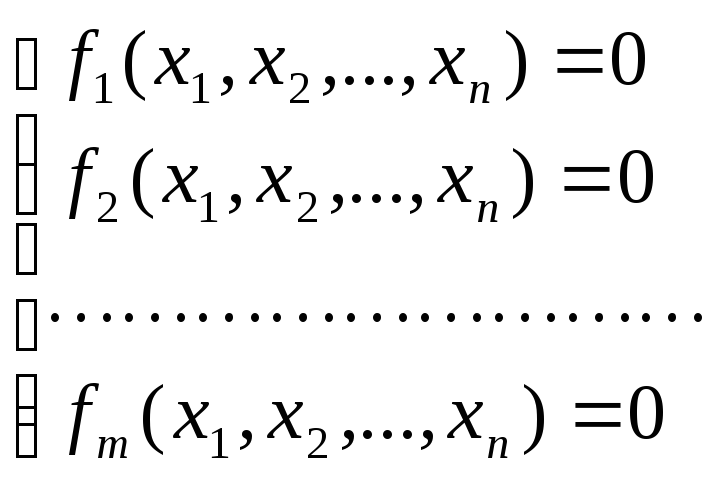 .
.