
- •2. Плановые государственные геодезические сети. Методы их создания
- •3) Развитие ггс
- •4.Развитие сетей сгущения. Плотность сетей сгущения
- •5. Требования к полигонометрии 4класса, 1 и 2 разряда
- •6. Технология полигонометрических работ
- •7.Создание проекта полигонометрических ходов и сетей.
- •8. Обработка результатов полевых измерений.
- •9. Критерии вытянутости(изогнутости) полигонометрического хода.
- •10. Центр тяжести полигонометрического хода. Определение тяжести графическим способом.
- •11 . Оценка точности проекта вытянутого полигон. Хода.
- •12. Оценка точности проекта изогнутого полигоном. Хода
- •15. Способ круговых приемов
- •16. Трехштативная система (тс).
- •18. . Линейные измерения в полигонометрии.
- •21. Ошибки центрирования и редукции
- •22.. Ошибка собственного измерения угла. Ошибки за влияния внешней среды.
- •23. Инструментальные ошибки.
- •25. Действие ошибок угловых и линейных измерений.
- •27. Веса и обратные веса результатов измерений в полигонометрии. (Определение весов и обратных весов измерений).
- •28. Определение числа избыточных измерений в полионом. Ходе.
- •29.Вывод первого условного уравнения поправок ждля полигонометрического хода
25. Действие ошибок угловых и линейных измерений.
Имеем
полигонометрический ход. В таком ходе
измерено n-число
сторон n+1-число
измеренных углов. αнач
– нач дирекц угол; αкон
– кон дирекц угол; x1
и y1
– координаты исходного пункта;xn+1
и yn+1
– коорд исх пункта n+1.
В следствии ошибок измеренные углы
будут ошибочно измерены на величины
αβ1,
αβ2,
αβ3,…,αβn+1;
αs1,
αs2,…,αsn.
Измеренные в ходе углы и наличие исход
данных позволяют вычислить угловую
невязку в ходе. fβ=Ʃβ-(αкон-αнач)
-180˚(n+1);
m2β=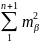 ;
mƩ
mβ
;
m2Ʃ=
m2β(n+1)+m2(αкон-αнач);
пред fβ=пред
dβ
;
пред dβ
=2mβ.
Полагая что пред fβ=
удвоенной сред квад ошибки измер угла.
;
mƩ
mβ
;
m2Ʃ=
m2β(n+1)+m2(αкон-αнач);
пред fβ=пред
dβ
;
пред dβ
=2mβ.
Полагая что пред fβ=
удвоенной сред квад ошибки измер угла.
Пред fβ =2mβ ; L=S1 + S2 +…+Sn; dL=dS1 + dS2 +…+dSn; m2L1=m2S1+m2S2 +…+m2Sn=[mS]
26.
27. Веса и обратные веса результатов измерений в полигонометрии. (Определение весов и обратных весов измерений).
Вес измерений – это величина обратно пропорциональная квадрату СКО(средней квадратической ошибке) измерения.
Pi=C/mi2 , где C – коэффициент пропорциональности. Он выбирается вычислителем в зависимости от удобства вычислений.
В полигонометрии, выполняемой с помощью тахеометра принято величину C принимать равной C=mβ2 , где mβ – СКО измерения углов, но т.к. в полигонометрии есть 2 вида измерения \углы и линии\, то mi=mβ , mi=mS ;
Вес измеренный углов Pβ i = mβ2/ mβ2=1
PS i = mβ2/ mS2
Обратный вес это величина обратная весу.
πβ i=1/ Pβ i=1
πS i=1/ PS i= mSi2/ mβi2
mS i=mS
mβi=mβ
28. Определение числа избыточных измерений в полионом. Ходе.
r=n-t
r- число избыт. Измерений
n – число всех выполненных измерений
t – число необход. Измерений.
t- определяется по числу пунктов умноженных на 2, т.к у каждого определяется 2 координаты.
(n+1)-2=(n-1)*2
t=2n-2
n+1 –углов, n- сторон
Всего вып. Измерений n=2n+1
r=2n+1-2n+2=3
Вывод: следовательно для хода опир. На 2 исходных пункта и 2 исход.направления число избыточных измерений всегда равно 3.
Следствие: В полигоном. Ходе данного вида число ур-ний в системе условных ур-ний связи, а так ж в системе условных ур-ний поправок, а так же в системе ур-ний корелат будет =3
29.Вывод первого условного уравнения поправок ждля полигонометрического хода
В
полигонометр. Ходе каждое избыточное
измерение приводит к матем. Соотношению
между истинными значениями измерений
велечин
в этом случае исходящая
система условных ур-ий связи будет иметь
вид:
𝜑i(Y1,
Y2,
Y2,…,
Yn)=0
i-
номер условия=1,2,3
Y1,
Y2,
Y2,…,
Yn-
истинное значение измер. Величин.
Первое
условие возникникающие в данном
ходе.
Анач.
дир. Углом нач. направления и конечного
направления.
𝜑1=
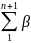 -[(Aнач-Aкон)+180o*(n+1)]=fβ;
(1)
второе
и третье усовие возникают из связей
приращения координат с исхлд. Нач и кон
пунктов.
𝜑1=
-[(Aнач-Aкон)+180o*(n+1)]=fβ;
(1)
второе
и третье усовие возникают из связей
приращения координат с исхлд. Нач и кон
пунктов.
𝜑1=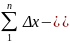 к-xн)=
к-xн)=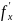 ;
(2)
𝜑3=
;
(2)
𝜑3=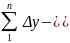 к-yн)=
к-yн)=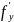 ;
(2)
Штрихи у невязок во 2 и 3 ур-ии
означает что эти невязки получ по
приращениям выч. По измер углам. Составим
в общем виде три условных ур-ия поправок,
система условных ур-ий поправок будет
выглядеть след образом:
[ai*Vi]+f1=0
[bi*Vi]+f2=0
(4)
[ci*Vi]+f3=0
В
этой системе Vi-
поправкик результатам измерений которые
надо найти решив сист (4)
ai,
bi,
ci
– коэффициенты при поправках
Обозначим
частные производные от 1-ой функции
;
(2)
Штрихи у невязок во 2 и 3 ур-ии
означает что эти невязки получ по
приращениям выч. По измер углам. Составим
в общем виде три условных ур-ия поправок,
система условных ур-ий поправок будет
выглядеть след образом:
[ai*Vi]+f1=0
[bi*Vi]+f2=0
(4)
[ci*Vi]+f3=0
В
этой системе Vi-
поправкик результатам измерений которые
надо найти решив сист (4)
ai,
bi,
ci
– коэффициенты при поправках
Обозначим
частные производные от 1-ой функции

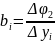 (5)
(5)
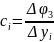
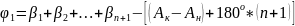
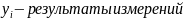 i=1,2,3…n+1
углов;
i=1,2,3…n+1
сторон;
i=1,2,3…n+1
углов;
i=1,2,3…n+1
сторон;
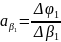 =+1;
=+1;
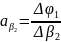 =+1;
=+1;
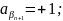 (6)
(6)
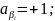
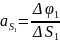 =0;
=0;
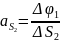 =0;
……………………..
=0;
……………………..
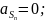
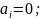 (7)
(7)
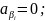 [
[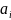 *
*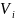 ]+
]+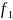 =0;
=0;
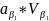 +
+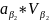 +…+
+…+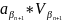 +
+ +
+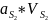 +…+
+…+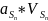 +
+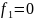 .
(8)
В ур-ие (8) подставим ур-ие
(7)
[
.
(8)
В ур-ие (8) подставим ур-ие
(7)
[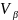 ]+
]+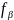 =0
(9)
Условное ур-ие (9) наз-ся условным
ур-ем поправок дирекционных углов.
=0
(9)
Условное ур-ие (9) наз-ся условным
ур-ем поправок дирекционных углов.
30) Вывод 2-го уравнение связи ϕ2=ΔX1+ ΔX2+…+ ΔXn-(Xк-Xн) (10) т.к. ΔXi=Si*cosAi (11) ϕ2= S1*cosA1 + S2*cosA2+…+Sn*cosAn- (Xк-Xн) (12) т.к. A1= Aнач+β1-180о;
A2= A1+ β2-180о=Aнач+ β1+ β2-180о*2 A3= Aнач+ β1+β2+ β3-180о*3 (13) An= Aнач+ β1+β2+…+ βn-180о*n (cos)=-sin (14)
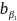 =
=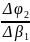 =S1*(-SIN
A1)+S2*(-SIN
A2)+…+Sn*(-SIN
An)=
(-Δy1)+(
-Δy2)+…+(
-Δyn)=
=S1*(-SIN
A1)+S2*(-SIN
A2)+…+Sn*(-SIN
An)=
(-Δy1)+(
-Δy2)+…+(
-Δyn)=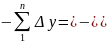 (+
yn+1-
y1);
(к)
(н)
(+
yn+1-
y1);
(к)
(н)
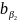 =(-Δy2)+(
-Δy3)+…+(
-Δyn)=
)=
=(-Δy2)+(
-Δy3)+…+(
-Δyn)=
)=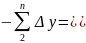 -(
yn+1-
y2);
-(
yn+1-
y2);
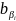 =-(
yn+1-
yi);
=-(
yn+1-
yi);
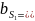
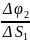 =COS A1;
=COS A1;
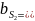 COS
A2;
…………………………….
COS
A2;
…………………………….
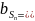 COS An;
Вывод:
все
=-(
yn+1-
yi);
COS An;
Вывод:
все
=-(
yn+1-
yi);
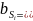 COS
Ai;
[bi*Vi]+fx=0
[VS(см)*COS
A]-
COS
Ai;
[bi*Vi]+fx=0
[VS(см)*COS
A]-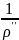 *[
*[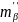 (yn+1-
yi(см))]+
(см)=0
Вывод
3 услов.
уравнения
аналогичны
1-му.
(yn+1-
yi(см))]+
(см)=0
Вывод
3 услов.
уравнения
аналогичны
1-му.
