Блок самопроверки:

Пример 1

. Единственным решением является пара чисел  х = 1, у = 2.

Пример 2.

. Решением этой системы будут любые два числа х и у, удовлетворяющие условию  у = 3 – х. Например, х=1, у=2;  х=0, у=3 и т. д.

Пример 3.

. Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.

Пример 4.

Решим методом Гаусса систему   

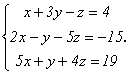
Вычтем из второго уравнения удвоенное первое, а из третьего – первое, умноженное на 5.

Получим: 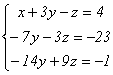 . Теперь вычтем из третьего уравнения удвоенное второе, а затем разделим второе уравнение на –7 (коэффициент при у), а третье – на 15 (новый коэффициент при z). Система примет вид:

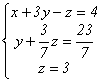                           .  Отсюда  z=3, y=2, x=1 – единственное решение системы.

Пример 5.

Система 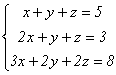 после исключения  х  из второго и третьего уравнений примет вид: 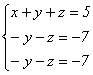. Если затем вычесть второе уравнение из третьего, то последнее уравнение станет тождеством 0=0. В системе осталось два уравнения: . Ее решение можно записать в виде:  х = -2, у – любое число, z = 7 – y. Таким образом, система имеет бесконечно много решений.

Пример 6.

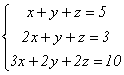. Применив к этой системе метод Гаусса, получим ,

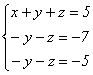откуда 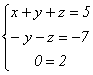. Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения.

Пример 7.

Рассмотрим систему , решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:

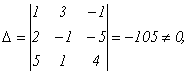 следовательно, система имеет единственное решение.

Отсюда

 

Пример 8.

 . Здесь 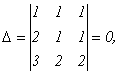 поскольку имеет два одинаковых столбца.

Следовательно, система не имеет единственного решения. Найдем  и

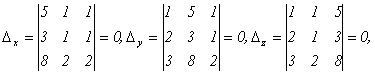поэтому система имеет бесконечно много решений.

 

Пример 9.

. Для этой системы  но

следовательно, решений нет.

Пример 10.

Найдем матрицу, обратную к 

следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:

 Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак,  Можно убедиться, что найденная матрица действительно удовлетворяет определению  Найдем

Тот же результат получим и при перемножении в обратном порядке.

Пример 11.

Вернемся к системе

Для нее

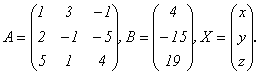
   Найдем :

Следовательно,

Таким образом, х = 1, у = 2, z = 3.

Список литературы:

1. Балдин, К.В. Краткий курс высшей математики / К.В.Балдин, Ф.К.Балдин, В.И.Джеффаль – М.: Дашков и Ко, 2009 (электронный ресурс «Университетская библиотека»);

2. Малыхин, В.И. Высшая математика: Учебное пособие / В.И.Малыхин – М.: Инфра-М, 2009 (электронный ресурс «Университетская библиотека»);

3. Самарин, Ю.П. Высшая математика / Ю.П.Самарин, Г.А.Сахабиева, В.А.Сахабиев – М.: Машиностроение, 2006 (электронный ресурс «Университетская библиотека»).

Глава 6. Теория пределов, непрерывные функции, разрывы

Определение предела последовательности

Определение 1. Последовательностью называется упорядоченное счетное множество чисел .

Обратите внимание, что

а) всего чисел - счетное множество и

б) они расположены в определенном порядке.

Над последовательностями можно проделывать некоторые операции.

а) Умножение последовательности на число.

Пусть дана последовательность и число c. Тогда произведением последовательности на число c называется последовательность вида .

б) Сложение и вычитание последовательности.

Пусть даны две последовательности и . Суммой и называется последовательность вида

+ = .

Разностью - последовательность видa

- = .

в) Умножение и деление последовательностей.

Произведение последовательностей

= .

Частное последовательностей

.

Определение 2. Последовательность называется ограниченной сверху, если

ограниченной снизу, если ;

ограниченной, если ;<

(последнее часто пишут так ).

Определение 3. Говорят, что при n стремящемся к бесконечности, последовательность сходится к пределу a (запись или ) если

Число а называют пределом последовательности .

В понятии “последовательность” впервые в математике нашло свое отражение движение. До введения этого понятия математика изучала лишь статитические объекты - площадь треугольника, 2x2 = 4 и т.д., и только в последовательности впервые находит свое отражение движение. Действительно, пусть - это моя координата на оси в какой-то - й момент времени. Тогда, идя по последовательности, я двигаюсь по оси - сначала я нахожусь в точке , затем перехожу в точку , затем в точку и т.д..

Конечно, движение бывает различным. Понятие предела отражает один из типов этого движения. Посмотрим еще раз на определение понятия предела, записав его в виде .

Вокруг точки a взята произвольная - окрестность . Сначала движение может быть произвольным, но вот на - м шаге последовательность попадает в эту - окрестность и все последующее движение происходит в этой - окрестности, т.е. попав на - м шаге в окрестность точки a, последовательность навсегда остается в этой окрестности. Так как сколь угодно мала, то это означает, что в своем движении мы неограниченно близко приближаемся к точке a и уже не можем уйти от нее. Понятие предела и отражает именно такой тип движения.

Дадим еще несколько похожих определений.

Определение 4. Говорят, что при последовательность сходится к пределу, равному (запись: или ) если

.

Это означает, что какое бы большое число мы не взяли, при своем движении на каком - то шаге мы окажемся правее точки и при дальнейшем движении всегда будем находиться правее этой точки.

Определение 5. Говорят, что при последовательность сходится к пределу, равному (запись: или если

.

Бесконечно-малые и бесконечно-большие последовательности

Определение 1. Последовательность называется бесконечно-малой последовательностью, если , т.е. если

.

Определение 2. Последовательность называется бесконечно-большой последовательностью, если (это записывается еще и так: , не учитывая знака перед ), т.е. если

.

Изучим некоторые свойства этих последовательностей.

1⁰. Сумма и разность бесконечно-малых последовательностей есть также бесконечно-малая последовательность.

Доказательство:

- б.м.п. =>

- б.м.п. =>

Возьмем . Тогда

откуда следует, что есть б.м.п.

Следствие. Сумма любого конечного числа б.м.п. ест также б.м.п

2⁰. Произведение б.м.п на ограниченную последовательность есть б.м.п.

Доказательство:

- ограничена. =>

- б.м.п. =>

.

Но тогда

отсюда и следует, что есть б.м.п.

3. Б.м.п. ограничена

Доказательство:

Пусть - б.м.п. Тогда .

Возьмем .

Тогда т.е. ограничена.

Следствие. Произведение б.м.п. есть также б.м.п.

4. Пусть - б.м.п. и . Тогда есть б.б.п.

Доказательство:

- б.м.п => .

Возьмем любое и положим .

Тогда

отсюда следует, что есть б.б.п.

5. Пусть - б.б..п, тогда есть б.м.п.

- б.б.п => .

Возьмем любое и положим

Тогда

отсюда следует, что есть б.м.п.

Предел монотонной последовательности

Определение. Последовательность называется

- монотонно возрастающей (неубывающей), если ;

- строго монотонно возрастающей (неубывающей), если ;

- монотонно убывающей (невозрастающей), если ;

- строго монотонно убывающей (невозрастающей), если ;

Монотонно возрастающие последовательности обозначают символом , монотонно убывающие - символом .

Теорема:

1. Если последовательность монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;

2. Если последовательность монотонно возрастает, но неограниченна сверху, то .

Доказательство.