11. Трение в кинематических парах. Динамические модели поступательной пары в плоском механизме с учетом трения.

Пусть при силовом расчете плоского механизма ставится задача определения реакций, лежащих в плоскости движения. При этом в идеальной поступательной паре неизвестными компонентами реакций будут (рис.5.4) сила R_y, перпендикулярная линии движения ползуна, и момент ; при наличии трения возникает еще одна компонента R_x.

а) б)

Рис. 5.4

Чтобы задача силового расчета оставалась разрешимой, эту третью компоненту необходимо выразить через первые две или выразить все три неизвестные составляющие через какие-либо два параметра. Сделать это можно различными способами, основываясь на разных предположениях относительно характера распределения нормальных сил по поверхностям соприкосновения. Предположим сначала, что эти силы распределяются некоторым образом по одной из двух контактных плоскостей, например, по нижней (рис.5.4, а). Если (х) – нормальная сила, приходящаяся на единицу длины линии контакта в точке с координатой х, то удельная сила трения , возникающая в той же точке, определяется из выражений (5.1) и (5.2):

(5.8)

Здесь функция (знак ) означает, что силы трения, действующие на ползун, направлены противоположно его скорости. Из (5.8) получаем

(5.9)

поскольку в данном случае

Таким образом, мы получили выражение, связывающее реакцию R_x с R_y и тем самым сводящее число неизвестных компонент реакций к двум. Отметим, что при соприкосновении ползуна и направляющей по верхней плоскости знак R_y изменится на противоположный, а знак R_x в силу (5.9) сохранится. В дальнейшем выражение (5.9) нам будет удобно представить в форме

(5.10)

с учетом того, что

Предположение о том, что контакты ползуна с направляющей происходят только по одной из плоскостей, не всегда оказывается приемлемым. Часто становится необходимым учитывать перекос ползуна, при котором контакт возникает на обеих плоскостях (рис.5.4, б). При этом 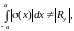и выражение (5.9) становится неверным.

В этом случае можно воспользоваться другой моделью поступательной пары. Примем условно, что нормальные силы, возникающие на поверхностях контакта, могут быть заменены двумя сосредоточенными силами N_A и N_B, приложенными в крайних точках ползуна. В зависимости от распределения нормальных сил (х) силы N_A и N_B могут быть приложены в точках А и B , либо в точках А’ и B’ и направлены соответственно либо вверх, либо вниз. Выразим теперь все три компоненты реакций кинематической пары через два параметра – N_A и N_B. Из рис.5.4, б получаем

(5.11)

(5.12)

Учитывая, что при переходе точки контакта с одной плоскости на другую направление силы трения не изменяется, а направление момента этой силы относительно точки 0 изменяется на противоположное, получаем

(5.13)

Отметим, что при отсутствии трения (f = 0) реакции N_A и N_B будут иметь разные знаки, если Это условие, вообще говоря, может рассматриваться как критерий, указывающий на необходимость использования модели, описываемой уравнениями (5.11)-(5.13).

Для более удобного запоминания сведем модели поступательных пар в табл. 5.1.

Таблица 5.1

	Без трения	Одноточечный контакт	Двухточечный контакт
Rx	0
Ry	Ry	Ry	NA + NB