8. Применение общего уравнения динамики для определения реакции в кинематической паре.

К онструктивными элементами, образующими высшую кинематическую пару, являются поверхности, принадлежащие сопрягаемым звеньям. В одних случаях эти поверхности в каждом положении механизма касаются в некоторой точке, в других – касание происходит по некоторой линии. При точечном контакте абсолютно твердых звеньев и при отсутствии сил трения реакции в кинематической паре сводятся к силе R_n, направленной по общей нормали к контактирующим поверхностям. Такая пара является пятиподвижной, и в ней возникает одна неизвестная компонента реакции (рис.4.12, а). При линейном контакте силы взаимодействия (при отсутствии трения) распределены вдоль линии контакта и направлены в каждой точке по общей нормали к поверхностям (рис.4.12, б).

В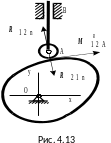 плоском кулачковом механизме (рис.4.13) линией контакта является прямая, силы взаимодействия лежат в одной плоскости и приводятся к главному вектору , направленному по нормали к поверхности кулачка, и главному моменту , вектор которого лежит в плоскости, касательной к профилю. В этом случае высшая кинематическая пара является четырехподвижной.

Аналогичная картина возникает в прямозубых и косозубых эвольвентных цилиндрических передачах. Здесь, правда, в зацеплении могут одновременно находиться несколько пар зубьев, но все силы контактного взаимодействия лежат в одной плоскости, проходящей через линию зацепления и параллельной осям вращения колес. В конических, червячных и гипоидных передачах линия контакта (если она существует) может оказаться пространственной. При этом и силы взаимодействия образуют пространственную систему: появляются дополнительные компоненты реакций, обычно оказывающиеся «лишними» неизвестными при составлении уравнений силового расчета. В таких случаях идут на упрощение модели кинематической пары, оставляя одну неизвестную компоненту реакции R_n и тем самым переходя к условной схеме точечного взаимодействия. Следует отметить, что при силовом расчете тяжело нагруженных зубчатых передач «жесткая» модель контактного взаимодействия без учета сил трения дает лишь весьма приближенные представления о силовых нагрузках. Чаще всего определение этих нагрузок, связанное с прочностными расчетами, опирается на более сложные модели силового взаимодействия, учитывающие упругую деформацию зубьев, влияние смазки и т.п. Однако рассмотрение таких моделей выходит за рамки этого курса.

9. Расчет кулачкового механизма методом кинетостатики и с помощью общего уравнения динамики.

Рассмотрим кулачковый механизм, состоящий из кулачка 1 и поступательно движущегося толкателя 2 (рис.4.14).

Механизм содержит две низших кинематических пары (O и B) и одну высшую (A). В плоскости движения во вращательной паре две неизвестных компоненты реакции – R_01x и R_01y, в поступательной – R₀₂ и , и в высшей кинематической паре – нормальная сила R_12n= – R_21n. Вместе с обобщенной силой Q имеем шесть неизвестных. Для их отыскания можем составить шесть уравнений кинетостатики, которые при равномерном вращении кулачка имеют следующий вид:

R_01x + Ф₁cos t + R_12nsin = 0,

R_01y + Ф₁ sin t – R_12n cos – G₁ = 0,

Q – R_12n ecos – R_12n sin (h₀ + s) – G₁ sin t = 0,

R₀₂ – R_12n sin  = 0,

R_12n cos – P – P_пр – Ф₂ – G₂ = 0,

Здесь  t – угол между радиусом 0С₁ (С₁ – центр масс кулачка) и осью x, ₁= 0С₁,  – угол давления, Ф₁ и Ф₂ – силы инерции кулачка и толкателя, G₁ и G₂ – силы тяжести, Р_пр – сила, создаваемая пружиной, прижимающей толкатель к кулачку.