27. Механические характеристики двигателей (пример с электрическим двигателем постоянного тока независимого возбуждения).

П ри решении задач динамики машин обычно используют наиболее простые динамические модели двигателей, отражающие зависимости между законами изменения во времени входного параметра двигателя (управления) u(t) , обобщенной координаты выходного звена q(t) и обобщенной движущей силы Q(t) (рис.8.1). Математические соотношения, описывающие эти зависимости, называются механическими характеристиками двигателей. К более сложным моделям, учитывающим динамику внутренних физических процессов, происходящих в двигателях, приходится обращаться сравнительно редко; в этом курсе такие модели рассматриваться не будут.

С основными разновидностями механических характеристик познакомимся на примере электродвигателя постоянного тока с независимым возбуждением, принципиальная схема которого показана на рис.8.2. Здесь вращение выходного звена двигателя (ротора) происходит за счет взаимодействия тока, возникающего в обмотке ротора, с магнитным полем, создаваемым обмоткой возбуждения . При вращении ротора в его обмотке в соответствии с законом электромагнитной индукции возникает обратная электродвижущая сила Е (ЭДС) , пропорциональная величине магнитного потока обмотки возбуждения Ф и угловой скорости ротора :

,

где – некоторый коэффициент пропорциональности. В цепи ротора при прохождении тока I возникают потери напряжения, связанные с наличием активного сопротивления R и индуктивности L . С учетом потерь уравнение электрической цепи записывается в форме

. (8.1)

С другой стороны, в соответствии с законом Ампера движущий момент Q связан с силой тока I соотношением

. (8.2)

Исключая I из (8.1) и (8.2), получаем

. (8.3)

Обозначив , , , легко преобразовать это выpажeниe к виду

. (8.4)

Соотношение (8.4) , связывающее входной ( ) и выходные ( ) параметры двигателя, называется динамической характеристикой. Параметр называется электромагнитной постоянной времени и характеризует инерционность электромагнитных процессов, происходящих в двигателе. Обычно величина его лежит в пределах от 0,02 до 0,1 с. Параметр называется крутизной характеристики двигателя. Чем больше крутизна , тем слабее изменение нагрузки влияет на величину угловой скорости ротора .

Характеристика (8.4) широко используется при анализе динамических процессов, происходящих в машинах, приводимых в движение электродвигателями постоянного тока с независимым возбуждением. Если исследуется статический процесс, при котором , выражение (8.4) упрощается и переходит в статическую характеристику двигателя:

.

Статическая характеристика может использоваться и для исследования таких динамических процессов , при которых , то есть в тех случаях , когда малой является либо постоянная времени , либо производная .

Н а рис.8.3 построены два семейства статических характеристик: на рис.8.3,а изображены рабочие характеристики, выражающие зависимости при различных постоянных значениях ; на рис.8.3,б представлены регулировочные характеристики , построенные для различных постоянных значений . В рассматриваемом случае все эти характеристики являются линейными.

Регулировочная характеристика, соответствующая Q = 0 ( то есть определяющая зависимость при отсутствии нагрузки на двигатель), называется характеристикой холостого хода. При определенных условиях эта характеристика может рассматриваться как приближенная и при . Это имеет место в тех случаях, когда статическая характеристика двигателя является достаточно жесткой, то есть когда крутизна s достаточно велика, так что влиянием нагрузки на скорость можно в первом приближении пренебречь. Характеристика. полученная при таком предположении, называется идеальной кинематической характеристикой; она может быть приведена к виду

. (8.5)

В соответствии с этой характеристикой угловая скорость ротора полностью определяется значением входного параметра двигателя: при ее использовании двигатель становится как бы "источником скорости”.

Общий вид механических характеристик двигателей. В общем случае механические характеристики различных двигателей (тепловых, гидравлических, пневматических) могут быть представлены в форме, аналогичной полученным выше. На холостом ходу , при , поведение двигателя характеризуется идеальной кинематической характеристикой

, (8.6)

которая в общем случае может быть нелинейной. С помощью такой характеристики приближенно описываются свойства двигателей, у которых скорость в статических режимах слабо зависит от нагрузки. Кроме рассмотренных выше электродвигателей такими свойствами обладают гидравлические двигатели с объемным и дроссельным управлением. В тепловых двигателях внутреннего сгорания и в пневматических двигателях наблюдается обратное: значение входного параметра u в значительной мере предопределяют величину обобщенной силы. Статические режимы в таких двигателях могут приближенно описываться идеальной силовой характеристикой

. (8.7)

В общем случае при исследовании статических режимов используются статические характеристики вида

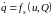. (8.8)

Они могут быть представлены в форме, разрешенной относительно Q:

. (8.9)

Эти характеристики учитывают влияние нагрузки на обобщенную скорость, которое в большей или меньшей степени проявляется у всех реальных двигателей. Регулировочные характеристики, получающиеся из (8.8) при Q=const, и рабочие характеристики, получающиеся из (8.9) при u=const, вообще говоря, являются нелинейными. Как правило с ростом нагрузки обобщенная скорость уменьшается, и рабочие характеристики оказываются “падающими”. Величина производной , взятая с обратным знаком

, (8.10)

называется крутизной статической характеристики в данной точке; для падающей характеристики . Если обобщенная скорость слабо зависит от нагрузки, статическая характеристика двигателя называется жесткой; если же изменение скорости слабо влияет на величину момента, характеристика является мягкой.

В некоторых задачах динамики машин значения и могут считаться близкими к некоторым средним значениям и . В этих случаях линейная статическая характеристика может быть линеаризована в окрестности точки ( , ):

. (8.11)

Статические характеристики адекватно отражают свойства реальных двигателей только при статических режимах работы машины, то есть в тех случаях, когда параметры постоянны или изменяются незначительно и достаточно медленно. В более общем случае приходится учитывать инерционность физических процессов, происходящих в двигателе. В электрическом двигателе постоянного тока такая инерционность связана с индуктивностью цепи якоря; она приводит к тому, что изменение входного напряжения не сразу влечет за собой изменение тока в цепи ротора; происходит переходный процесс, продолжительность которого зависит от постоянной времени .

В двигателях других типов у инерционности иная физическая природа. В гидравлическом двигателе она обусловлена сжимаемостью жидкости. Однако во всех случаях она приводит к тому, что обобщенная скорость выходного звена зависит не только от нагрузки, но и от ее производных по времени. В первом приближении это можно учесть введением в статическую характеристику (8.9) первой производной от и представлением ее в форме

. (8.12)

Параметр называется в общем случае собственной постоянной времени двигателя, а выражение (8.12) – его динамической характеристикой. Необходимо отметить, что для некоторых классов двигателей характеристика вида (8.12) может использоваться только в тех случаях, когда изменяется в сравнительно узких пределах, а для исследования других динамических режимов необходимо пользоваться более сложными динамическими моделями, которые в этом курсе не рассматриваются.