7.Средние величины, виды средних. Научные основы расчета средних величин.

 Наиболее распространенной формой статистических показателей является средняя величина.

     Средняя величина характеризует тип явления. Она одна может охарактеризовать всю совокупность, отразив наиболее типичное для этой совокупности значение признака.

    Или, средняя величина — типический уровень варьирующего признака.

     Как правило, средние характеризуют размер признака на единицу совокупности.

     Средняя — одна из наиболее часто используемых в обыденной жизни статистических величин. Например, каждый рабочий знает, что расчет отпускных производится исходя из средней заработной платы за последние три месяца, поступающие в вузы — что такое пропускной балл и т.д.

     В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные влиянием различных условий развития отдельных единиц, значение средней отражает наиболее типичное значение. В отличие от средней, абсолютная величина, отражающая значение признака у отдельной единицы совокупности, не позволяет сравнивать значение признака у единиц, относящихся к разным совокупностям.

Для того, чтобы средняя выполняла основное свое назначение — характеристика типа, при ее расчете должны выполняться следующие требования:

• средняя должна быть рассчитана в пределах однородной совокупности (качественно однородные совокупности позволяет получить метод группировок);

• расчет общих средних должен подкрепляться расчетом групповых средних;

• должна быть правильно выбрана единица совокупности, для которой определяется средняя;

• должна быть обеспечена достаточная наполненность групп или совокупности, по которой рассчитывается средняя величина. Чем больше объем совокупности, тем более точной будет рассчитанная средняя (закон больших чисел).

Средние величины делятся на два больших класса:

• степенные средние;

• структурные средние.

• К известным степенным средним относят среднюю арифметическую, среднюю гармоническую, среднюю геометрическую, среднюю квадратическую.

•       Структурные средние — мода и медиана.

•      Общая формула средней степенной выглядит следующим образом:

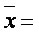
•      где

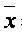
  	— средняя;
  x	— индивидуальное значение варьирующего признака;
  f	— частота, которая показывает сколько раз встречается значение осредняемого признака в данной совокупности.

•      В зависимости от k определяется вид средней (табл. 2). Кроме того, вид средней определяется по сгруппированным или несгруппированным данным. Именно в том случае, если средняя величина определяется по несгруппированным данным, получают простую среднюю, если по сгруппированным — то взвешенную.

•      Смысл средней взвешенной можно проиллюстрировать на следующем примере:

9.Структурные средние и их применение в статистике.

Мода и медиана определяются структурой распределения. Они позволяют определить среднюю величину без производства вычислений, визуально. Их используют в том случае, когда расчет степенных средних невозможен или нецелесообразен.

     В дискретном ряду распределения мода определяется визуально. Например, распределение семей по числу детей:

1 ребёнок	25
2 ребёнка	30
3 ребёнка	10
4 и более детей	2

     В данном ряду распределения мода равна 2, то есть в данной совокупности наиболее часто встречаются семьи с двумя детьми. Очень удобно использовать этот показатель для характеристики наиболее часто встречаемого значения признака, определяемого по большой совокупности. Например, наиболее часто спрашиваемый размер обуви, размер одежды и т.д.

     В интервальном ряду распределения, когда наиболее часто встречаемое значение признака задано в виде интервала, а мода должна отражать конкретное значение признака, используется следующая формула расчета:

     где

xмо	— мода;
x0	— верхняя граница модального интервала;
h	— величина интервала;
fмо, fмо-1, fмо+1	— частоты модального, предмодального и послемодального интервалов.

Медиана — варианта, которая делит ранжированный ряд распределения на две равные части. По обе стороны от медианы находится одинаковое число единиц совокупности.В дискретном ряду распределения медиана определяется визуально. Ряд признаков ранжируется, то есть значения признаков упорядочиваются по возрастанию или убыванию. Варианта, которая делит упорядоченный ряд пополам, будет медианой.

     Медиана в интервальном ряду распределения определяется по формуле:

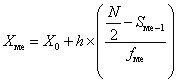
     где

xме	— медиана;;
x0	— верхняя граница медианного интервала;
h	— величина интервала;
N =  fi	— общая численность;
Sме-1	— накопленные частоты предмедианного интервала;
fме	— частота медианного интервала.

     В качестве медианного берется интервал, в котором находится единица совокупности, которая делит упорядоченный по значению признака ряд пополам. Для того чтобы определить медианный интервал, рассчитывают накопленные частоты. Последняя накопленная частота показывает общее количество единиц совокупности.