33. Порядок силового расчёта.

Исходные данные для силового расчета: Кинематическая схема механизма, Инерционные характеристики , Закон движения входного звена , Силовое нагружение.

Порядок силового расчета является обратным порядку кинематического исследования, т.е. силовой расчет начинается с последней (считая от ведущего звена) присоединенной группы и кончается силовым расчетом начального звена.

1. Кинематическое исследование и определение ускорений центров масс всех звеньев механизма, угловые ускорения всех вращающихся и плоско движущихся звеньев.

2. Определение сил и моментов инерции. В общем случае, когда тело совершает плоское движение, все силы инерции приводятся к главному вектору и главному моменту сил инерции, который в свою очередь раскладывается на пару сил. Если движение тела поступательное, то главный момент сил инерции равен нулю, если вращение вокруг закрепленного центра масс – то главный вектор сил инерции равен нулю.

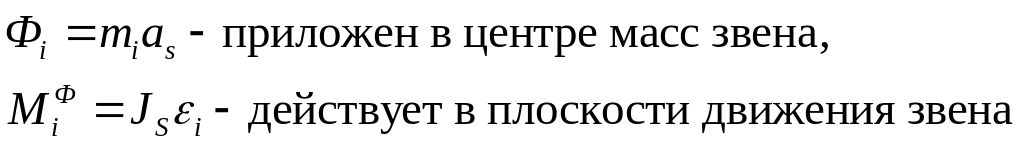
3. Расчленить механизм на структурные группы.

4. Применить принцип Д’Аламбера для структурных групп и отдельных звеньев: при движении механической системы активные силы, силы реакций связей вместе с силами инерции образуют равновесную систему сил для каждой точки системы. Таким образом, в конкретный момент времени можно к рассматриваемой системе применять уравнения статики:

При этом, если все моменты разложены на пары сил, а расчетные схемы построены в одном масштабе, то плечи для определения моментов берутся с чертежа в мм, а за положительное направление поворота принимают направление против часовой стрелки. Для нахождения сумм сил строятся планы сил в определенном масштабе, который может быть различным для различных расчетных схем.

5. Просчитать уравновешивающую нагрузку методом рычага Жуковского и сравнить со значением, полученным методом расчленения.

34. Рычаг Жуковского.

Для применения этого метода необходимо повернуть план скоростей на (рекомендуется поворачивать в сторону противоположную ). Переносим все заданные силы, действующие в рассматриваемый момент времени на звенья механизма, в том числе и силы инерции, в одноименные точки повернутого плана скоростей, не изменяя при этом величины и направления этих сил. (Силы реакции в Рычаге Жуковского не участвуют!) Составляем уравнение моментов всех перенесенных сил относительно полюса плана скоростей, т. е. рассматриваем план скоростей как некоторый рычаг с опорой в полюсе плана скоростей, находящийся под действием всех рассматриваемых сил в равновесии. Плечи всех сил берутся непосредственно с чертежа в мм.

Подобная геометрическая интерпретация принципа возможных перемещений представляет значительные удобства для решения многих задач динамики механизмов. Метод этот получил название метода Жуковского по имени ученого, которым он был предложен, а рычаг, которым пользуются в этом методе, назван рычагом Жуковского.

Метод Жуковского может быть применен для нахождения величины какой-либо одной неизвестной силы из числа сил, входящих в уравнение моментов, если точка приложения и направление этой силы заданы, а также заданы величины, направления и точки приложения всех остальных сил. В самом деле, в этом случае в записанном уравнении будет только одна неизвестная величина искомой силы, которая из него и определится.