
- •4. Метод варьирования свободных интегральных функционалов
- •4.1. Аналитические возможности метода
- •4.2. Постановка основной задачи мвсф
- •4.3. Модель задающих варьируемых воздействий
- •4.4. Физический смысл и энергетические аспекты управления
- •4.5. Нахождение системы уравнений переключающей функции управления
- •4.6. Конструирование кврегуляторов на основе метода варьирования свободных интегральных функционалов
- •4.6.1. Конечновременные передаточные функции
- •4.6.2. Структурные схемы квпередаточных функций с учетом нулевых начальных условий.
- •4.6.3. Структурные схемы кврегуляторов
4.3. Модель задающих варьируемых воздействий
Модель входного воздействия, построенная на основе метода варьирования свободных интегральных функционалов, будем называть моделью входного варьируемого воздействия.
Метод варьирования
свободных функционалов синтезирует
функцию управления: находятся моменты
переключения
![]() при заданном максимальнодопустимом
управлении, либо находятся моменты
переключения
при заданном максимальнодопустимом
управлении, либо находятся моменты
переключения
![]() и значения управления
и значения управления
![]() при
заданном конечном времени
при
заданном конечном времени
![]() .
На рисунке 4.1÷4.3 изображена функция
управления симметричная относительно
оси времени и симметричная относительно
заданного уровня. Математически функция
управления представляется следующим
выражением:
.
На рисунке 4.1÷4.3 изображена функция
управления симметричная относительно
оси времени и симметричная относительно
заданного уровня. Математически функция
управления представляется следующим
выражением:
![]() (4.18)
(4.18)
где
![]()
оптимизирующая функция управления.
оптимизирующая функция управления.
Оптимизирующим
действием функция управления обладает
благодаря ее варьированию во времени.
Запишем вариации для ограничений
![]() :
:
![]() (4.19)
(4.19)
где
![]() вариация
n-го порядка. Тогда
запишем (4.18) в более компактной форме :
вариация
n-го порядка. Тогда
запишем (4.18) в более компактной форме :
![]() (4.20)
(4.20)
Вариации (4.19)
представляют собой временные вариации
функции управления и обладают
следующим свойством: в них моменты
переключения являются основными искомыми
параметрами, погрешность которых зависит
от точности определяемых параметров
объекта управления, при оптимальном
синтезе. При этом вариация управления,
а вместе с ней и оптимизирующая функция
![]() выполняет
генераторную функцию. Она генерирует
управляющие сигналы в определенной
временной последовательности, и тем
самым весь процесс синтеза осуществляется
через текущую функцию времени
и ее запаздывающих функций
выполняет
генераторную функцию. Она генерирует
управляющие сигналы в определенной
временной последовательности, и тем
самым весь процесс синтеза осуществляется
через текущую функцию времени
и ее запаздывающих функций
![]() .
Здесь
.
Здесь
![]()
запаздывающий аргумент времени.
запаздывающий аргумент времени.
4.4. Физический смысл и энергетические аспекты управления
При изучении объекта управления возникают определенные цели. Желаемая цель может быть достигнута, если спроектированная система управления будет отвечать заданным требованиям. Выбор наилучшего управления зависит от принятого критерия, в качестве которого принимается функционал.
Важным оптимальным критерием является критерий максимального быстродействия. Оптимальные по быстродействию системы позволяют повысить производительность машин, станков и технологического оборудования. Такие системы имеют не только минимальное время переходного процесса, но и, как правило, наименьшую динамическую ошибку регулирования.
Управление по быстродействию имеет ясный физический смысл, который связан с балансом энергии в объекте управления [5, 8, 12].
Уравнение баланса энергии в объекте, когда совершается в нем переходный процесс, можно представить в виде суммы основных двух составляющих
![]() , (4.21)
, (4.21)
где
![]()
полезная работа, совершаемая в объекте;
полезная работа, совершаемая в объекте;
![]()
работа, которую необходимо затратить
на преодоление инертности объекта за
время переходного процесса.
работа, которую необходимо затратить
на преодоление инертности объекта за
время переходного процесса.
Работа совершается только при свободном движении. При подключении источника энергии к объекту в нем запасается энергия. Этот вид энергии играет важную роль в системах управления.
Переходя к мощности
![]()
и выделяя время, получаем выражение
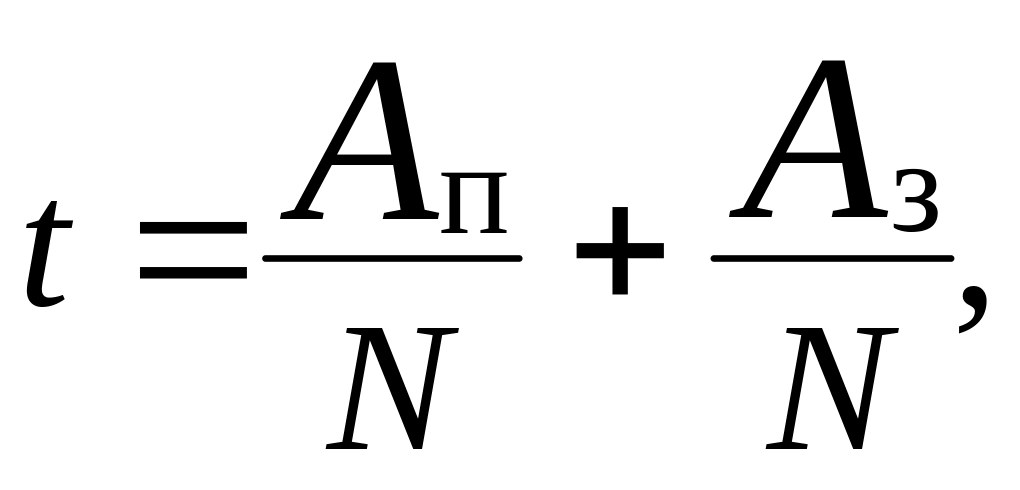
из которого видно, что увеличение мощности приводит к ускорению процесса запасания энергии в объекте.
В МВСФ вводят
интегральный функционал от функции
свободной составляющей с пределом
интегрирования от 0 до ¥
и номинальнозаданным
управлением
![]()
![]() (4.22)
(4.22)
где
![]()
свободная составляющая, соответствующая
корню характеристического уравнения
свободная составляющая, соответствующая
корню характеристического уравнения
![]() , i=1,
2, ..., n.
, i=1,
2, ..., n.
Будем называть функционал (4.22) номинальнозаданным или просто НЗфункционал.
После этого вводят понятие конечновременного интегрального функционала от той же свободной составляющей , который обозначим через КВфункционал. Для получения конечновременного управления необходимо задаться максимальнодопустимым управлением и выполнять варьирование его во времени. И затем приравнять функционалы
"КВфункционал"="НЗфункционал" (4.23)
Очевидно, что выражение (4.23) характеризует динамический баланс переходного процесса, так как функционалы представляют собой площади, соответствующие кривой переходного процесса с бесконечным временем (НЗфункционал) и кривой переходного процесса с конечным временем (КВфункционал).
Номинальнозаданный функционал, который также называется исходным функционалом.
Пример 4.1. Апериодический объект первого порядка.
Динамический процесс в нем описывается дифференциальным уравнением
![]() , (4.24)
, (4.24)
где
![]()
управляемая переменная (координата);
управляемая переменная (координата);
![]()
управление (управляющее воздействие);
Т
постоянная времени объекта;
управление (управляющее воздействие);
Т
постоянная времени объекта;
![]()
коэффициент передачи объекта.
коэффициент передачи объекта.
Для получения
НЗфункционала
зададимся номинальнозаданным
управлением
![]() ,
единичным коэффициентом передачи
,
единичным коэффициентом передачи
![]() и примем нулевые начальные условия при
и примем нулевые начальные условия при
![]()
![]() .
.
Тогда решение уравнения (4.24) запишется
![]() (4.25)
(4.25)
Здесь
![]() корень уравнения.
корень уравнения.
На рис.4.4 показаны изменения координат x(t) и u(t).
а)
б)
в)
Рис.4.4. Изменения координат x(t) и u(t): а) номинальнозаданное управление; б) переходная временная функция (переходный процесс); в) свободная составляющая переходного процесса.
Кривая, изображенная на рисунке 4.4в), характеризует свободную составляющую переходного процесса
![]()
Площадь
![]() равна
равна
![]()
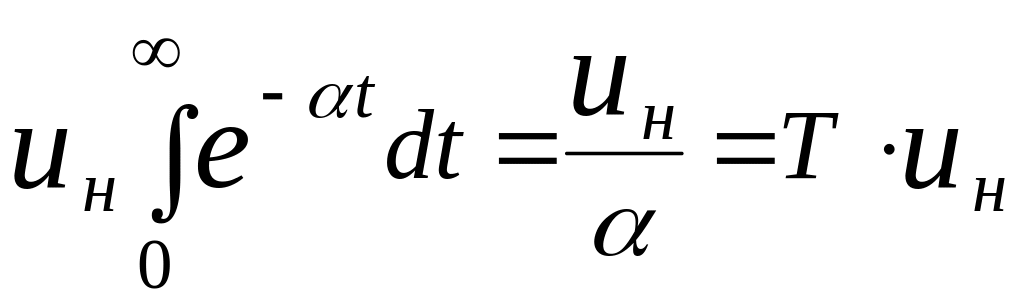 .
.
Таким образом
![]() есть НЗфункционал
или
есть НЗфункционал
или
![]() .
.
Очевидно, что площадь пропорциональна запасенной энергии в самом элементе. Это легко подтверждается примером электрической цепи, содержащей последовательно включенные индуктивность и сопротивление. Для этого примера x будет соответствовать току i, а u приложенному напряжению, и выражение (4.25) примет вид
![]()
где
![]() ;
;
;
;
![]()
постоянная времени,
постоянная времени,
![]() .
.
Если взять половину
произведения
![]() ,
то получаем известную формулу
,
то получаем известную формулу
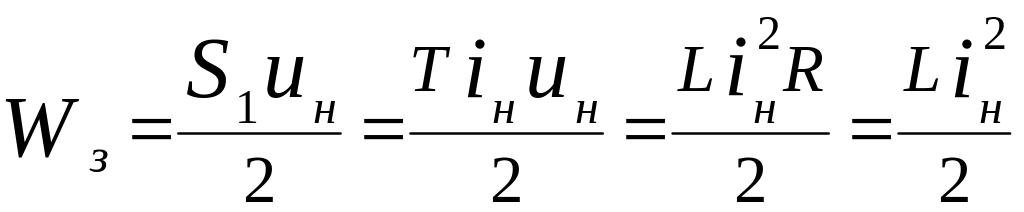 ,
,
которая характеризует величину магнитной энергии, запасенной в индуктивности за время переходного процесса.
Таким образом, индуктивная катушка является приемником электрической энергии, которая запасается в магнитном поле.
Другим примером является электрическая цепь, содержащая последовательно включенные конденсатор и сопротивление. Для такой цепи запасенная энергия в конденсаторе в виде электрического поля равна
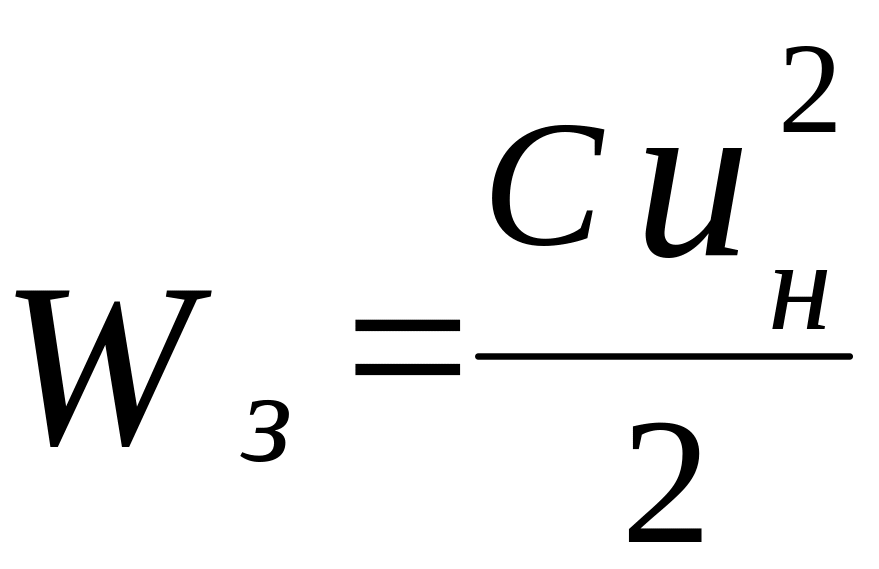 ,
,
где С емкость конденсатора; приложенное к цепи постоянное напряжение.
Пример 4.2. Апериодический объект второго порядка.
Имеет два действительных отрицательных корня:
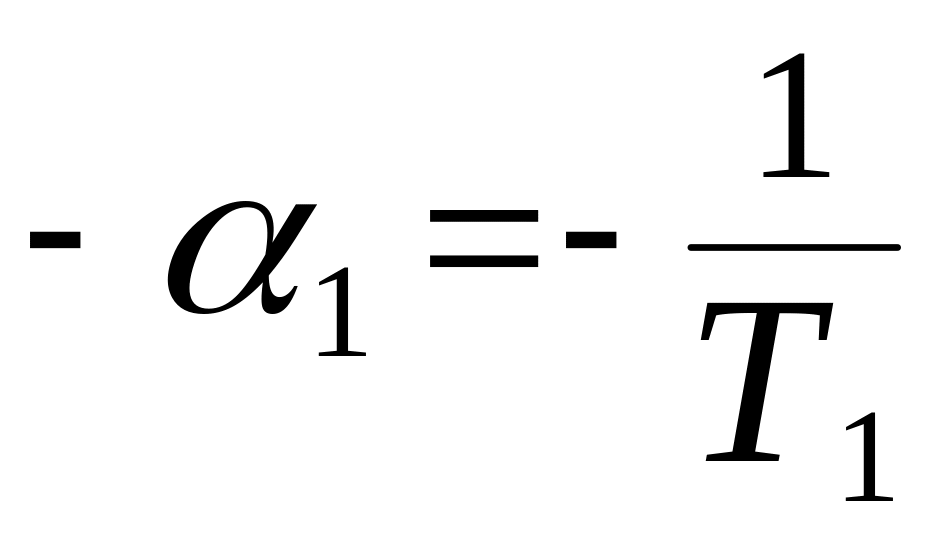 и
и
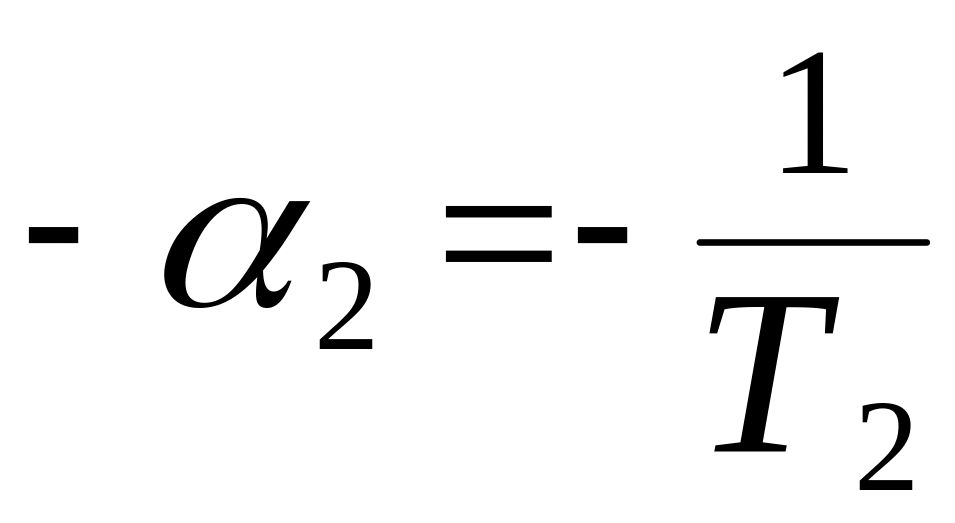 ,
где
,
где
![]() и
и
![]()
постоянные времени объекта.
постоянные времени объекта.
Запишем для такого объекта уравнение:
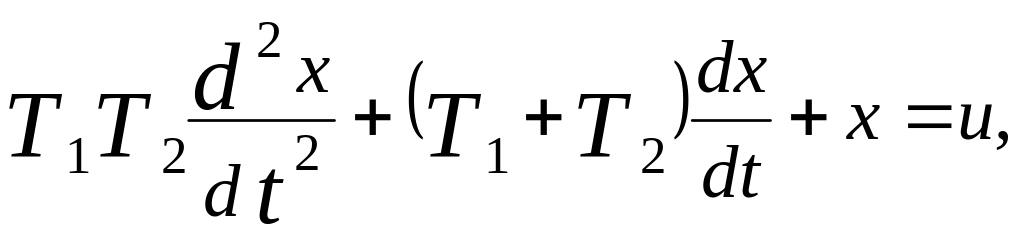
и его решение при нулевых начальных условиях и номинально заданном управлении
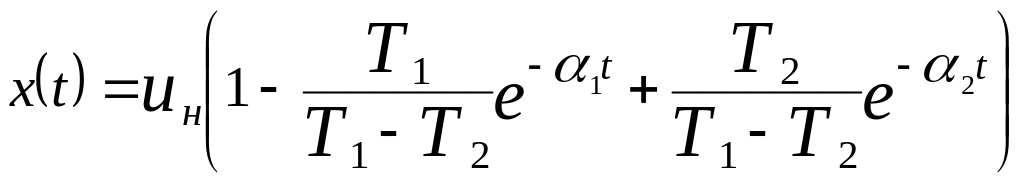 (4.26)
(4.26)
Решение (4.26) записано
для случая, когда
![]() .
Для объекта второго порядка получается
две свободных составляющих
.
Для объекта второго порядка получается
две свободных составляющих
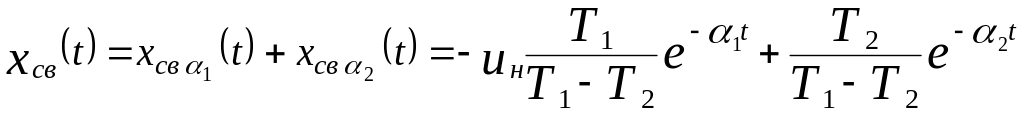
Номинальнозаданные функционалы будут равны
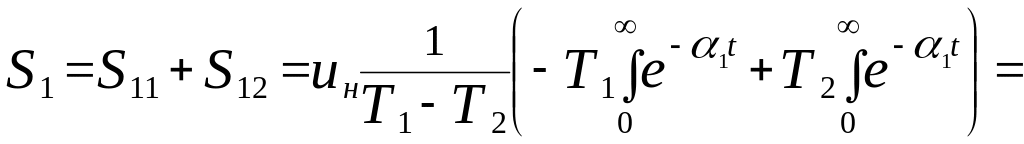
=![]() .
.
Тогда можно записать:
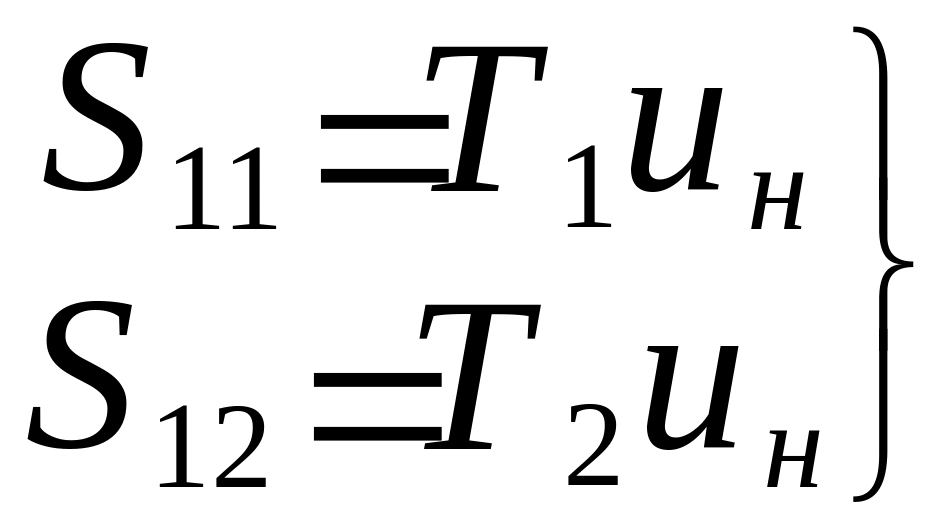 .
.
Получили два функционала
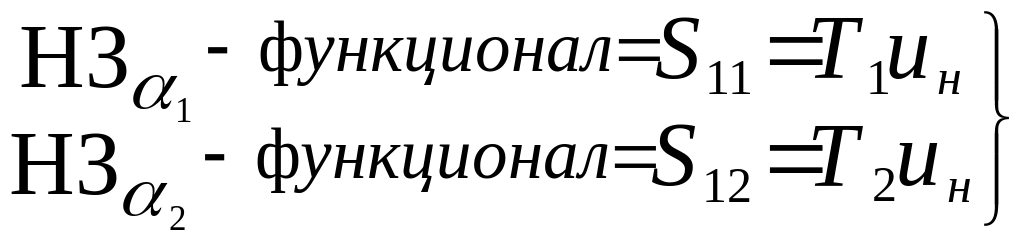 (4.27)
(4.27)
Для объекта n-го
порядка с n действительными
отрицательными корнями общая площадь
![]() и НЗфункционал
равны:
и НЗфункционал
равны:
![]() (4.28)
(4.28)
![]() ,
i = 1, 2, ...,
n (4.29)
,
i = 1, 2, ...,
n (4.29)
Из выражений (4.27÷4.29) видно, что для ускорения процесса накопления энергии и увеличения быстродействия системы управления необходимо сумму постоянных времени сделать наименьшей. В этом нет ничего нового. Так поступают в задачах синтеза систем с использованием традиционных методов годографа или интегральных оценок, и в некоторых современных методах пространства состояния, например методах теории модального управления.
МВСФ использует полученные выражения в качестве исходных, на основе которых формируется уравнение динамического баланса (2.2.6), критерий оптимальности по быстродействию и базовая вариация функционала.
