4. Метод варьирования свободных интегральных функционалов

4.1. Аналитические возможности метода

Синтез системы оптимального автоматического управления с критерием оптимальности по быстродействию выполняется, как уже отмечалось ранее, на основе принципа максимума Л.С. Понтрягина и метода динамического программирования [11, 4]. Однако, практическое применение этих методов сталкивается с большими трудностями вычислительного характера из-за того, что процесс построения оптимального управления сводится к решению краевой задачи для обыкновенных дифференциальных уравнений, либо дифференциальных уравнений в частных производных, что приводит к сложным математическим процедурам с использованием численных методов и повышенных требований к машинным ресурсам (время, память). Эти методы имеют аналитическое решение для простых задач (объекты 23-го порядка).

Современная теория оптимального быстродействия получила свое развитие в принципе конечновременных вариаций предельного быстродействия [12]. Данный принцип, в отличии от принципа максимума, также использует критерий оптимальности по быстродействию, но он имеет другую форму представления закона управления, при которой сохраняются интегралы, но с весьма простой подынтегральной функцией в виде свободной составляющей вынужденного движения переходного процесса. На основе такой преобразовательной формы разработан метод варьирования свободных интегральных функционалов (МВСФ) [2], который является прикладным методом проектирования нового класса конечновременных регуляторов [2, 3].

Наиболее важной характерной особенностью метода является введенная новая вариация интегрального типа

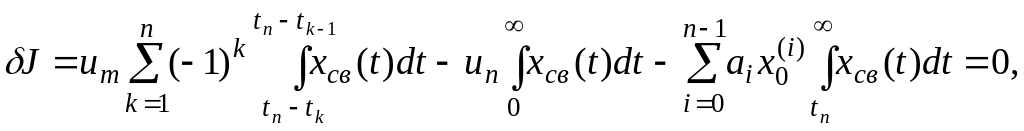
(4.1)

где ;  номинальнозаданное управление;  максимальнодопустимое варьируемое управление;  свободная составляющая переходного процесса ;  начальные значения управляемой переменной и ее производных;  коэффициенты зависящие от параметров объекта управления.

В вариации (4.1) первый функционал представляет собой закон управления

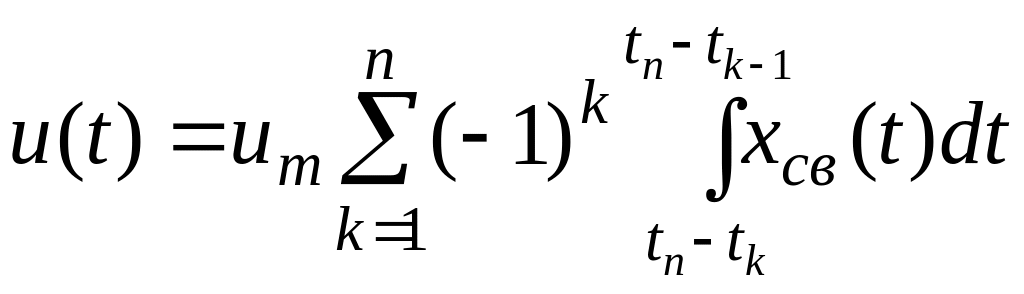(4.2)

Из выражений (4.1) и (4.2) следует, что для решения задачи оптимального быстродействия необходимо найти моменты переключения . В принципе максимума Понтрягина проблема моментов переключения управления решается с помощью вспомогательной функции , которая вместе с управлением составляет часть функции Гамильтона

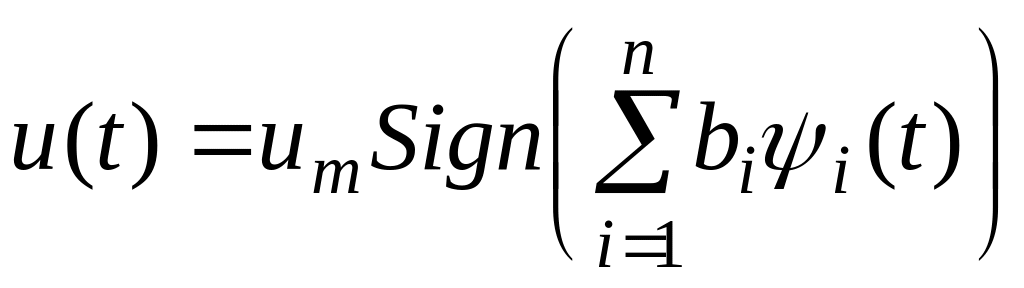
Однако математическая процедура нахождения функции представляет собой сложную задачу из-за того, что отсутствует начальное условие этой функции. Предложенный подход в виде конечновременного функционала (4.2) обладает двумя преимуществами. В нем выделены отдельно переключения , и, во-вторых, подынтегральные функции являются свободными составляющими переходного процесса. Интегралы (4.1) и (4.2), как правило, являются табличными интегралами.

Второй интеграл вариации (4.1) является исходным функционалом с той же свободной составляющей, но с пределами интегрирования от 0 до для номинальнозаданного управления и от до для начальных условий.

Выражения (4.1) отличается от всех известных вариаций интегрального типа, и является конечновременной вариацией (КВВ). Принцип конечновременных вариаций (ПКВВ) отличается от всех известных интегральных принципов по виду вариации функционалов. В нем варьирование функционалов выполняется за счет изменения пределов интегрирования, тогда как в известных вариациях интегрального типа варьирование функционалов происходит путем изменения подынтегральной функции. Оно используется для построения оптимального программного управления на конечном интервале времени без учета возмущений со стороны изменения параметров объекта и входных воздействий.

Однако реальное движение системы, как правило, будет отличаться от программного по многим причинам: из-за неполной информации о внешних возмущениях, неточности модели объекта и т.д. Поэтому необходимо еще учесть отклонения управляемой переменной и её производных от программного

(4.3)

и отклонение реального управления от программного

(4.4)

В результате получаем уравнение возмущенного движения с учетом неточности модели объекта на интервале времени :

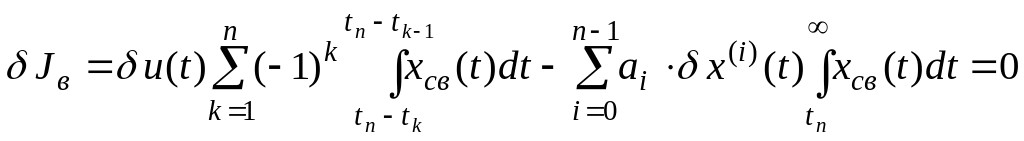
(4.5)

Выражения (4.1÷4.5) составляют основу математической модели моделирования линейных оптимальных систем управления по быстродействию. К этим выражениям необходимо еще добавить временные функции переходного процесса и их производные . Причем, учитывая, что моделирование в основном выполняется в цифровом варианте, то следует перейти к решетчатым функциям , где T  период дискретности.

МВСФ позволил снизить сложность синтеза систем управления, достигнуть высокого качества оптимального управления, минимизировать время перевода системы из начального в конечное состояние, добиться оптимального демпфирования по быстродействию. Это позволило реализовать работоспособный алгоритм идентификации с большим запасом надежности, быстрой сходимостью и обоснованными результатами.