3.4.1. Задача оптимального управления линейными стационарными объектами

Рассмотрим объект управления, движение которого описывается системой линейных дифференциальных уравнений с постоянными коэффициентами:

, (i=1,2,…,n) (3.16)

В векторной форме система уравнений (3.16) запишется:

, (3.17)

где  n-мерный вектор координат состояния; 

r-мерный вектор управления;

матрица размера n×n;

 матрица размерности n×r.

Для системы (3.17) будем полагать, что она полностью управляемая по отношению к каждой из компонент U₁(t), U₂(t),…, U_r(t) вектора управления U(t). Такие системы называются нормальными. Для того чтобы линейная система с постоянными коэффициентами вида (3.19) была нормальной, необходимо и достаточно, чтобы все матрицы:

, (j=1,2,…,r) (3.18)

были не вырождены. Здесь B_j – j-тый столбец матрицы В.

Каждая нормальная матрица является полностью управляемой.

Функция Гамильтона Н для рассматриваемой задачи (3.16) будет представлена в виде:

или в векторной форме:

Сопряженная система уравнений для вспомогательных переменных будет

(3.19)

Согласно принципа максимума оптимальное управление должно доставлять максимум функции Н. Рассматривая выражение (3.18) мы видим, что от управления U зависит только второе слагаемое, поэтому оптимальное управление должно максимизировать слагаемое , имеем:

Каждая составляющая вектора управления U изменяется независимо от остальных. Поэтому выражение (3.19) достигает максимума, если принимает значения:

, (к=1,2,…,r) (3.20)

Таким образом, оптимальное управление будет кусочно-постоянной функцией времени со значениями, принадлежащими вершинам r-мерного куба. Каждая составляющая есть кусочно-постоянная функция, принимающая значение ±1 в зависимости от знака

.

Если система (3.16) нормальна, то соотношение (3.20) однозначно определяют для каждого ненулевого вектора управляющие функции , причем эти функции имеют на отрезке [0;t_n-1] конечное число переключений (рис. 3.10).

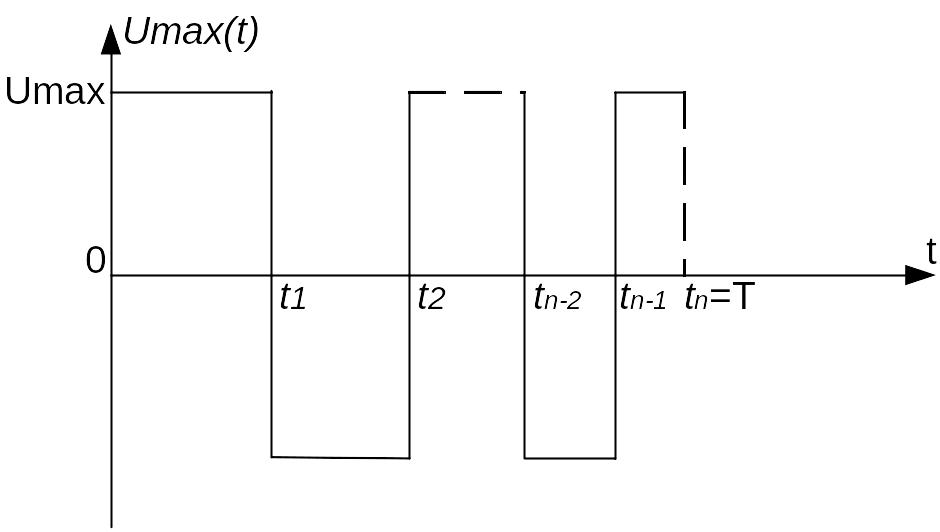
Рис. 3.10. Кусочно-постоянная функция управления Umax(t) для общего случая.

Выражение (3.20) является законом оптимального управления с кусочно-постоянной функцией, с числом переключения (n-1), где n – порядок объекта управления (3.16). В момент времени t=t_n управляющее воздействие Umax(t) выключается. Следовательно, общий интервал управления включает в себя n – интервалов.

3.4.2. Теорема об n – интервалах

В общем случае число переключений оптимального управления конечно.

Моменты переключения и число их зависит от многих факторов:

• от вектора состояния объекта в начальной x₀ и конечной x_k точках;

• от параметров, характеризующих объект управления, т.е. от постоянного времени объекта и коэффициента передачи;

• от вектора возмущающих воздействий (помех) и других факторов.

Мы будем рассматривать случаи, когда все характеристические числа матрицы А действительны, область управления представляет собой r-мерный куб и отсутствуют возмущающие воздействия.

Теорема 3.1. Если характеристические числа матрицы А – действительные числа и область управления U представляет собой r-мерный куб, то каждое из управлений кусочно-постоянно и имеет не более (n-1) переключений, где n- порядок системы.

Теорема об (n-1)- переключениях (об n – интервалах) справедлива только для линейных объектов с действительными корнями. Теорему еще называют теоремой о числе переключений.