14 . Разновидности интеллект систем.:

1)Интеллектуально информационно-поисковые системы-явл система взаимод с проблемно-ориентир БД на естеств языке

2)Экспериментные системы-

3)Расчетно логические системы-позволяют решать управленческие и проэктные задачи по их описанию и исходным данным вне зависимости от сложности модели.Каждому пользователю предоставл возможно контролировать выполнение процесса.основные свойства реализованы б знаний.

4)гибридные системы.в них представлена возможность учета характеристик мира.

15.Принятие решений в условиях риска.

В этих условиях выбираемая стротегия управления связана с множеством возможных исходов,причем кажд исход имеет вероятность появления,заранее известного ЛПР.В этих условиях для решения используют два правила.

-Искусственное сведение к детерминированию:

-оптимизация в среднем: заключается в переходе от исход показател эффективности явления к её усредненной статичной характеристике.исходный показатель эффективности опис формулой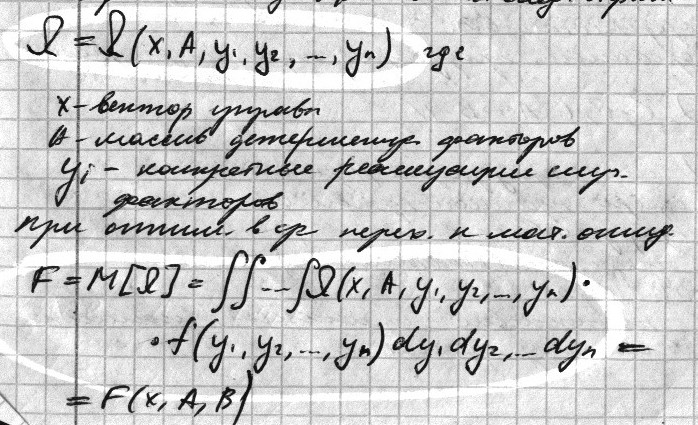

В-массив известных статич характеристик используемых величин

f-закон распределения вероятностей

16.Условия неопределённости.Критерии Лапласа,Вальда.

Отсутствует однозначная связь между выбоом стротегии и решением.В общем случае неопределенность может быть вырожена либо противодействием разумного противника,либо недостаточн освеломленностью об условиях в котор осуществл выбор решения.принятие решения в условиях различных противодействующ теорий.

Критерий Лапласа

П оскольку вероятности возможной или иной ситуации неизвестны,предпологают что они равновероятностны,тогда для каждой строки матрицы выполн подстановка сред арифметич значений оценок.оптимал решению соответств такое которое соответств максимальному знач сред арифметич

.

Критерий вальда

В каждой строке матрицы выбир мин оценка.оптимальное решение соответств то,котор дает максимум этого минимума

Критерий гурвица

При реализации вводят коэфиц оптимизации 0<(альфа)<1. В каждой строке матрицы находят самые большие оценки и минимальные оценки max aij min aij

Они умножаются на альфа и 1-альфа соответственно.оптимал решение которое max этой суммы.

Критерий севиджа

В каждом столбце матриц находят max оценку max aij и составл новые матрицы элементы котор определяются соответств

Rij=max aij-aij

Выбор значен при котор матриц риска принимает минимал значения.критерий заключается в минимизации риска.

17.Многокритериальные задачи принятия решений.

Чаще принимаем решения рассматр в качестве совокупности критериев f1,f2… каждый из этих критериев характериз коэффициентом относительно важности лямда1, лямда2…. Совокупность критериев образует интегральный критерий F={fk}

Каждый критерий характериз какое либо качество приним решения. Оптимал решение может быть условно записано след образом

F-оптимал критерия. X-оптимал значен управляемого параметра. Лямда-вектор важности. Wx-ОДЗ.

ОДЗ Wxможно разбить на 2 непересек подобласти.

1)Wxc-область согласия,в которой качество приним решений может быть улучшена по одному или несколк критериям.

2)Wxk область компромиссов.

Принцип равномерности.

В ыбирается такое вариант решения, при котором дост равномерность показателей по всем критериям.использ след реализацию:

А)принцип равенства

В этом случае выб вариант при котор все значения критериев равны между собой

Б)------------ max min

F*=optF=maxmin fij для каждого из вариантов выбир min значен критерия.выбирается вариант в котором этот min достигает max/равномерность обеспеч за счет подтягивания критериев с наименьшим значением показателея

В)------------ квариравентсва

Так как не удается достич принципа равенста,то используется этот.лучшим признается вариант в котором критерии наиболее близки к этому равенству.