11

Определение графа

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.

Плоские графы

Граф, который можно изобразить на плоскости без пересечения ребер вне вершин, называется плоским топологическим графом.

Область плоскости, ограниченная ребрами и не содержащая в себе вершин или ребер, называется гранью графа.

Формула Эйлера. Если связный плоский топологический граф имеет n вершин, m ребер и f граней , то n-m+f=2.

На географической карте (принимаем за ребра участки границ государств, а за вершины - их стыки).

Пример:

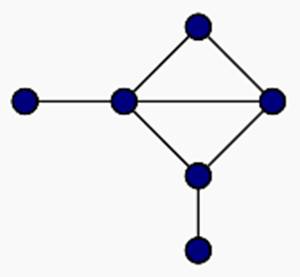
Эйлеровы графы

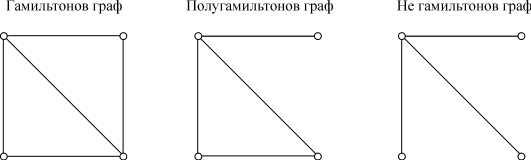
Эйлеровым путем в графе называется путь, содержащий все ребра графа. Граф называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро. Такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым, при этом каждый эйлеров граф будет полуэйлеровым.

Примеры.

Задачи с эйлеровыми графами часто встречаются в книгах по занимательной математике — например, можно ли нарисовать какую-нибудь диаграмму, не отрывая карандаша от бумаги и не проходя никакую линию дважды. Название "эйлеров" возникло в связи с тем, что Эйлер первым решил знаменитую задачу о Кенигсбергских мостах, в которой нужно было узнать, имеет ли граф, изображенный на рисунке, эйлерову цепь (не имеет!).

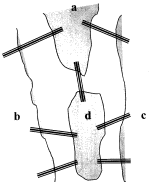
В 1736 г. великий Леонард Эйлер (1707-1783), свыше 30 лет работавший в Петербургской Академии наук (1727-1741, 1766-1783) нашел решение головоломки о кенигсбергских мостах. Дело в том, что в Кенигсберге было два острова, соединенных семью мостами с берегами реки Прегель и между собой (рис.15). Жители города мечтали найти замкнутый маршрут прогулки по всем мостам, но их попытки были безуспешны.

Рис.15

Для того, чтобы отвлечься от красот природы и зодчества, Эйлер рисует мультиграф (рис.16) и, наряду с поставленной задачей, ставит вопрос о возможности нарисовать эту фигуру, не отрывая пера от бумаги и не проводя линий дважды.

Рис.16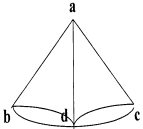

Цепь, проходящую через все вершины графа только по одному разу, называют эйлеровой (соответствующая замкнутая цепь называется эйлеровым циклом).

Результат Эйлера практически стал краеугольным камнем топологии и теории графов. Область его применения - от поиска маршрута по выставочным залам Эрмитажа до психологических тестов и конструирования компьютеров.

Гамильтоновы пути и контуры

В 1857 г. ирландский математик Вилльям Гамильтон (1805-1865) предложил игру "путешествие по додекаэдру" (рис.14а), где нужно было прогуляться по ребрам через все вершины, не попадая ни в одну из них дважды (додекаэдр - многогранник, гранями которого служат пятиугольники - 20 вершин и 30 ребер). При желании додекаэдр можно (вырезав грань АBCDE) развернуть на плоскости (рис.14b) и обнаружить достаточно простой порядок перехода (рис.14с).

Рис.14

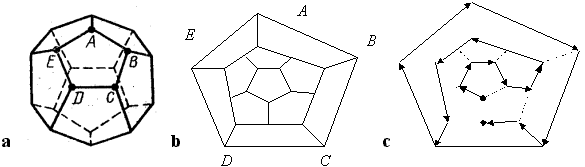
Путь, проходящий через все вершины графа только по одному разу, называется гамильтоновым. Если он замкнут (конец пути совпадает с его началом, говорят о гамильтоновом контуре.

В полном графе (любая пара вершин соединена путем хотя бы в одном направлении) всегда есть гамильтонов путь

Эйлеровы и гамильтоновы пути сходны по способу задания. Первые содержат все ребра, по одному разу каждое, вторые - все вершины, по одному разу каждую. Но, несмотря на внешнее сходство, задачи их поиска резко отличаются по степени трудности. Для решения вопроса о наличии эйлерова цикла в графе достаточно выяснить, все ли его вершины четны. Критерий же существования гамильтонова цикла в произвольном графе еще не найден.

Орграф

Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках (Оре) и просто рёбрами.

Существует большое количество задач, решаемых на орграфах. Чаще всего рассматриваются задачи о достижимости (т.е. о существовании пути, связывающем две заданные вершины), о нахождении путей, обладающих какой-либо экстремальной характеристикой (например, кратчайший, или наиболее надежный путь), о случайных блужданиях, потоковая задача. Все они хорошо изучены и разработаны эффективные алгоритмы их решения. При этом предполагается, что все пути на графе являются допустимыми, т.е. не накладывается никаких ограничений на достижимость.

Наиболее известные работы в этой области принадлежат Кристофидесу Н., Басакеру Р.Д., Харари Ф., Бержу К., Дейкстре Э., Флойду Р., Замбицкому Д.К., Оре О., Саати Т., Фалкерсону Д.Р., Форду Л.Р.

В отличие от классического подхода, Басанговой Е.О. и Ерусалимским Я.М. было введено понятие ориентированных графов с нестандартной достижимостью, т.е. орграфов, в которых на допустимые пути накладываются какие-либо ограничения. В обычном ориентированном графе, для того чтобы одна вершина была достижима из другой, необходимо существование пути, связывающего две эти вершины. В случае же орграфов с нестандартной достижимостью требуется, кроме того, чтобы этот путь удовлетворял некоторому условию (ограничению). Понятно, что в этом случае классические алгоритмы решения задач на графах непосредственно неприменимы.

Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V,A), для которой выполнены следующие условия:

V это множество вершин или узлов,

A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v w ведёт от вершины v к вершине w.

Формально, орграф D=(V, E) есть множество E упорядоченных пар вершин .

Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.

Орграф, полученный из простого графа (Простой граф — граф, в котором нет кратных рёбер и петель.) ориентацией ребер называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.

Направленный полный граф называется турниром. Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с n вершинами имеет n(n − 1) / 2 рёбер и обозначается Kn. Является регулярным графом степени n − 1.