
- •1 Электрический заряд и его свойства. Законы сохранения и квантования заряда. Взаимодействия зарядов. Закон Кулона. Характеристики неточечных зарядов.
- •2.Электрическое поле, его характеристики- напряженность, индукция и потенциал. Графическое изображение полей. Поле точечного заряда. Сложение электрических полей.
- •3.Метод вычисления напряженности. Применение принципа суперпозиции для вычисления электрических полей неточечных зарядов. Напряжённость электрического поля точечного заряда
- •4.Поток напряженности электрического поля. Теорема Остроградского-Гаусса. Примеры применения теоремы Гаусса для расчета электрических полей.
- •Циркуляция вектора напряженности
- •6.Связь между напряженностью эл. Поля и потенциалом. Градиент потенциала. Вычисление потенциала для неточечных зарядов.
- •7.Микроскопическое строение диэлектрика. Жесткий и мягкий диполь в электрическом поле.
- •8.Поляризация диэлектрика. Вектор поляризации, диэлектрическая восприимчивость. Поверхностные связанные заряды.
- •9.Электрическое поле в диэлектрике. Физический смысл относительной диэлектрической проницаемости. (Связь векторов поляризации, напряженности и индукции).
- •10.Сегнетоэлектрики, диэлектрический гистерезис, домены. Пьезоэлектрический эффект.
- •11.Проводники. Условия равновесия зарядов в проводнике. Распределение избыточных неподвижных зарядов в проводнике.
- •Равновесное распределение зарядов на проводниках.
- •12.Проводники во внешнем электрическом поле. Возникновение наведенного заряда на проводнике.
- •13.Электроемкость. Емкость шара. Заземление. Емкость конденсатора, системы конденсаторов.
- •14. Энергия системы точечных зарядов. Энергия заряженного проводника. Энергия эл. Поля. Плотность энергии эл. Поля.
- •15.Постоянный электрический ток. Основные понятия: сила тока, эдс, напряжение, разность потенциалов, сопротивление проводника и полупроводника.
- •]Эдс индукции
- •Электрический ток в полупроводниках
- •16.Закон Ома в интегральной форме для однородного и неоднородного участков и замкнутой цепи. Закон Ома в дифференциальной форме .
- •2.3 Законы Ома в интегральной форме
- •2.3.1 Закон Ома в дифференциальной форме
- •18. Классическая электронная теория электропроводности. Вывод закона Ома.
- •19.Вывод закона Джоуля-Ленца. Недостатки классической теории.
- •20. Правила Кирхгофа. Их применение в расчета сопротивления проводников. Первый закон
- •Второй закон
- •21. Магнитное поле. Вектор магнитной индукции. Напряженность магнитного поля. Закон Био-Савара-Лапласса.
- •22.Применение закона Био-Савара-Лапласса для расчета индукции магнитного поля прямого тока.
- •23.Применение закона Био-Савара-Лапласса для расчета индукции магнитного поля в центре на оси кругового тока. Магнитный момент кругового тока.
- •24. Закон Ампера. Взаимодействие прямых длинных параллельных токов.
- •Два параллельных проводника
- •25.Магнитный диполь. Поведение магнитного диполя в однородном и неоднородном магнитном поле.
- •26.Вихревой характер магнитного поля. Закон полного тока, его применение для расчета магнитного поля соленоида и тороида. Вихревой характер магнитного поля
- •27. Магнитный поток. Теорема Гаусса для магнитного поля. Работа, совершаемая при перемещение проводника и рамки с током в магнитном поле.
- •Теорема Гаусса для магнитной индукции
- •28. Сила Лоренца, ее характеристики. Формула Лоренца. Движение заряженных частиц в магнитном и электрическом поле.
- •29.Эффект Холла, его объяснение.
- •Свойства
- •30.Магнетики. (Электронные микротоки в атоме). Прецессия электронов в атоме в магнитном поле. Магнитные свойства атомов и молекул.
- •Определение
- •Магнитный момент атома
- •31.Магнитное поле в веществе, сущность намагничивания. Вектор намагничивания. Магнитная восприимчивость и относительная магнитная проницаемость вещества.
- •32. Виды магнетиков(диамагнетики, парамагнетики, ферромагнетики) Зависимость их свойств от напряженности магнитного поля.
- •33.Ферромагнетики. Явление гистерезиса. Домены(в 10 вопросе). Точка Кюри.
- •34. Явление электромагнитной индукции. Закон Фарадея. Правила Ленца. Связь явления эми и закона сохранения энергии.
- •Физическая суть правила
- •35. Причины возникновения эдс индукции в неподвижном контуре, вращающимся контуре, движущимся проводнике.
- •36.Явление самоиндукции. Эдс самоиндукции. Индуктивность. Изменение тока в цепи при включении эдс.
- •38.Применение явления эми. Токи Фуко. Скин-эффект. Явление взаимной индукции. Трансформаторы.
- •39.Энергия магнитного поля. Плотность энергии магнитного поля.
- •40.Колебательный контур без активного сопротивления. Свободные электрические колебания. Параметры колебаний.
- •Характеристики
- •41.Затухающие электрические колебания. Логарифмический декремент затухания.
- •42.Вынужденые электрические колебания. Переменный ток.
- •43.Резонанс напряжений. Резонанс токов. Мощность в цепи переменного тока.
- •44.Электромагнитное поле. Теория Максвелла. Понятие о токе смещения.
- •[Править]Точная формулировка
- •45.Интегральные уравнения Максвелла.
- •46.Электромагнитные волны. Излучение эмв. Свойства эмв. Шкала эмв.
- •Шкала электромагнитных волн
Два параллельных проводника

Наиболее
известным примером, иллюстрирующим
силу Ампера, является следующая задача.
В вакууме на расстоянии ![]() друг
от друга расположены два бесконечных
параллельных проводника, в которых в
одном направлении текут токи
друг
от друга расположены два бесконечных
параллельных проводника, в которых в
одном направлении текут токи ![]() и
и ![]() .
Требуется найти силу, действующую на
единицу длины проводника.
.
Требуется найти силу, действующую на
единицу длины проводника.
Бесконечный проводник с током в точке на расстоянии создаёт магнитное поле с индукцией:
![]() (по закону
Био — Савара — Лапласа).
(по закону
Био — Савара — Лапласа).
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
![]()
По
правилу буравчика, ![]() направлена
в сторону первого проводника (аналогично
и для
направлена
в сторону первого проводника (аналогично
и для ![]() ,
а значит, проводники притягиваются).
,
а значит, проводники притягиваются).
Модуль данной силы ( — расстояние между проводниками):
![]()
Интегрируем,
учитывая только проводник единичной
длины (пределы ![]() от
0 до 1):
от
0 до 1):
![]()
25.Магнитный диполь. Поведение магнитного диполя в однородном и неоднородном магнитном поле.
ДИПОЛЬ
МАГНИТНЫЙ -аналог диполя
электрического,
к-рый можно представлять себе как два
точечных магн. заряда ![]() ,
расположенных на расстоянии l друг
от друга. Характеризуется дипольным
моментом, равным по величине
,
расположенных на расстоянии l друг
от друга. Характеризуется дипольным
моментом, равным по величине![]() и
направленным от
и
направленным от ![]() .
В предельном случае
.
В предельном случае ![]() принято
говорить о точечном или элементарном
Д. м. Понятие Д. м. возникло в кон. 18 -нач.
19 вв., когда для объяснения
природы магнетизма предполагалось
существование магн. материи. Впоследствии
оно сохранило своё значение как удобная
модель, позволяющая правильно вычислять
поля соленоидальных электрич. токов.
Если объёмная плотность тока
принято
говорить о точечном или элементарном
Д. м. Понятие Д. м. возникло в кон. 18 -нач.
19 вв., когда для объяснения
природы магнетизма предполагалось
существование магн. материи. Впоследствии
оно сохранило своё значение как удобная
модель, позволяющая правильно вычислять
поля соленоидальных электрич. токов.
Если объёмная плотность тока ![]() чисто
соленоидальна
чисто
соленоидальна ![]() ,
её можно выразить через вектор намагниченности
,
её можно выразить через вектор намагниченности ![]() ,
представляющий собой плотность магнитного
момента
,
представляющий собой плотность магнитного
момента ![]() ,
так что магн. момент всей системы
токов
,
так что магн. момент всей системы
токов ![]() равен:
равен:
![]()
В однородном разворачивается по полю, а в неоднородном еще движется в место с наибольшей плотностью маг. поля.
26.Вихревой характер магнитного поля. Закон полного тока, его применение для расчета магнитного поля соленоида и тороида. Вихревой характер магнитного поля
Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.
ЗАКОН ПОЛНОГО ТОКА один из основных законов электромагнитного поля. Устанавливает взаимосвязь между магнитной силой и величиной тока, проходящего через поверхность. Под полным током понимается алгебраическая сумма токов, пронизывающих поверхность, ограниченную замкнутым контуром.
Намагничивающая
сила вдоль контура равна полному току,
проходящему сквозь поверхность,
ограниченную этим контуром. В общем
случае напряженность поля на различных
участках магнитной линии может иметь
разные значения, и тогда намагничивающая
сила будет равна сумме намагничивающих
сил каждой линии.
![]()
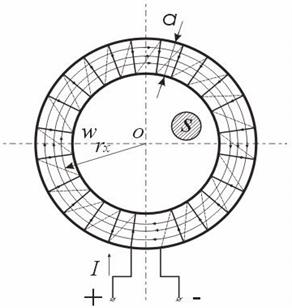
Обмотка имеет W витков и обтекается током I. Магнитные линии внутри кольца представляют собой концентрические окружности с центров точке О. Применим к контуру Cх, совпадающему с одной из магнитных линий, проходящих в магнитопроводе, закон полного тока. При этом будем считать:
 и
и 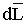 совпадают,
следовательно α = 0;
совпадают,
следовательно α = 0;величина Нх во всех точках контура одинакова;
сумма токов, пронизывающих контур, равна IW.
Тогда![]() .
.
Отсюда [А/м],
[А/м],
где Lx – длина контура, вдоль которого велось интегрирование; rx – радиус окружности.
Вектор внутри кольца зависит от расстояния rх. Если α – ширина кольца << d, то эта разница между значениями Н в пределах сердечника не велика. При этом в расчет допустимо принять для всего поперечного сечения магнитопровода одно значение напряженности магнитного поля:
Hср = IW / L , где L – длина средней магнитной линии.
Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник. Тороид можно рассматривать как длинный соленоид, свернутый в кольцо (рис. 4.1).

Длина соленоида l содержит N витков и по нему протекает ток I. Считаем соленоид бесконечно длинным. Эксперимент показал, что внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю).
Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, охватывающему все N витков, согласно (4.12) равна:
![]() .
(4.14)
.
(4.14)
Интеграл ![]() можно
представить в виде суммы двух интегралов:
по внутренней части контура:
можно
представить в виде суммы двух интегралов:
по внутренней части контура: ![]() и
по внешней:
и
по внешней: ![]() ,
тогда из (4.14) получим:
,
тогда из (4.14) получим:
![]() ,
(4.15)
,
(4.15)
 или
или ![]() , (4.16)
, (4.16)
где В –
индукция магнитного поля внутри
соленоида;  –
число витков на единицу длины соленоида.
–
число витков на единицу длины соленоида.
