
Тема 1
Введение в дисциплину. Основные понятия и определения. Проявление случайности. Случайность и закономерность. Применение и полезность статистических методов в контроле качества, анализе дефектов и исследовании технологических процессов.
Тема 2
Взаимосвязь статистики и качества. Формирование статистического мышления.
Рассмотрение основных примеров и положений теории вероятности.
Знакомство с программным обеспечением Statistica. Практическая работа № 1 – «Описательная статистика и графики».
Тема 3
Правило трех сигм. Погрешности измерений как источники случайности.
Решение задач
Законы распределения случайных величин. Практическая работа № 2 – «Законы распределения. Подбор закона распределения по экспериментальным данным».
Тема 4
Простые методы для контроля качества.
Рассмотрение примеров применения инструментов контроля качества. Практическая работа № 3 – «Диаграмма Парето». Расчет и построение диаграммы Исикавы.
Тема 5
Проверка статистических гипотез.
Практическая работа № 4 – «Проверка статистических гипотез».
Тема 6
Оценка параметров случайных величин. Точечные и интервальные оценки.
Практическая работа № 5 – «Точечная и интервальная оценки параметров распределения».
Тема 7
Контрольные карты: Правила выбора вида контрольной карты. Алгоритмы построения контрольных карт
Практическая работа № 6 – «Контрольные карты Шухарта». Индивидуальное задание № 2. Построение контрольных карт
Тема 8
Виды, назначения и области применения специальных контрольных карт.
Кумулятивные контрольные карты. Карты медиан
Индивидуальное задание № 3. Построение и анализ специальных контрольных карт
Тема 9
Анализ измерений и состояния процессов. Показатели качества процессов Статистическое регулирование технологических процессов, статистический контроль производства. Способы наглядного представления (визуализации) качества процесса. Метод 6 сигм. Практическая работа № 7 – «Оценка воспроизводимости процесса».
Тема 10
Семь новых инструментов управления качеством Примеры применения инструментов управления качеством.
Бенчмаркинг. Менеджерские методы. Выполнение группового задания. Тест по ранее пройденным темам.
Тема 11
Развертывание функций качества (QFD). Методика построение дома качества. Выполнение групповых заданий.
Тема 12
Основы надежности. Анализ характера и последствий отказов (FMEA)
Основы теории надежности. Анализ характера и последствий отказов ( метод FMEA). Порядок определения ПЧР. Выполнение групповых заданий
Тема 13
Выборочный контроль Оперативная характеристика. Планы выборочного контроля. Виды контроля.
Практическая работа № 8 – «Выборочный контроль».
Тема 14
Анализ временных рядов
Тема 15
Взаимосвязь инструментов качества и рекомендации по их применению. Методика (из семи шагов) по внедрению статистических методов на предприятии. Обзор области применения статистических методов, приведенных в национальном стандарте ГОСТР ИСО 10017:2003.
Третий вопрос в билете практический:
Тема 1
Задание 1 . Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X— числа появлений события в этих испытаниях.
Решение. По условию, n=10, p=0,6.
вероятность непоявления события q=1-0,6=0,4.
Искомая дисперсия
D(X)= n∙p∙q=10∙0,6∙0,4=2,4.
Задание 2
Случайная величина X задана законом распределения; где
р- вероятность появления значения
-
X
2
3
10
р
0,1
0,4
0,5
Найти среднее квадратическое отклонение σ (X).
Решение. Найдем математическое ожидание X:
M (X) = 2∙0,1+3∙0,4 + 10∙0,5 = 6.4.
Найдем математическое ожидание X2:
М (Х2) = 22∙0,1 +32∙0,4+102∙0,5 = 54.
Найдем дисперсию:
D(X)=M(X2)-[M(X)]2= 54— 6,42= 13,04.
Искомое среднее квадратическое отклонение:
σ (X)=![]() =
=
![]() ≈3,61.
≈3,61.
Задание 3
Среднее квадратическое отклонение отдельного измерения σ=6. Всего произведено 36 измерений (n = 36).
Найти среднее квадратическое отклонение среднего арифметического 36 измерений .
σ (![]() )=σ/
)=σ/![]() =6/
=6/![]() =1.
=1.
Определить какой из параметров, указанных в примере, ближе к истинному значению измеряемой величины ?
Это- среднее арифметическое нескольких измерений, так как σ ( ) =1 , а для отдельного измерения σ=6.
Задание 4
Найти дисперсию случайной величины Х, которая задана следующим законом распределения. где р- вероятность появления значения
-
X
1
2
5
р
0,3
0,5
0,2
Решение. Найдем математическое ожидание:
М{Х)= 1-0,3+2.0,5 + 5.0,2 = 2,3.
Найдем все возможные значения квадрата отклонения:
[x1-M(X)] 2=(1-2,3) 2=1,69;
[x2-M(X)] 2=(2-2,3) 2=0,09;
[x3-M(X)] 2=(5-2,3) 2=7,29.
Напишем закон распределения квадрата отклонения:
-
[X — М (Х)]2
1,69
0,09
7,29
р
0,3
0,5
0,2
D(X)= 1,69-0,3 + 0,09 0,5 + 7,29-0,2 = 2,01.
Тема 2 и 3
В чем отличие S от
Расшифровать формулу:
![]()
Записать формулу перестановки

Записать формулу размещений

Записать формулу сочетаний

Дописать формулу:
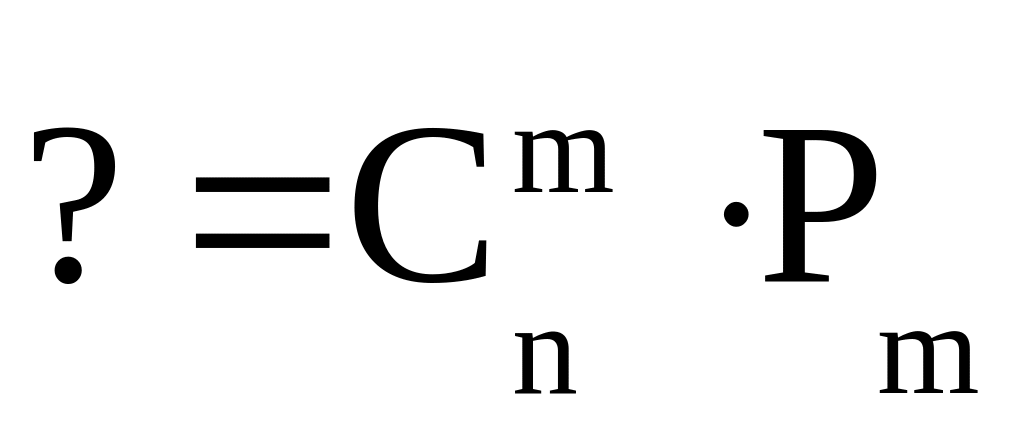
Задачи
1. Геометрическое распределение задает вероятность того, что…?
Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель p = 0,7. Найти вероятность того, что попадание произойдет при втором выстреле.
2. Гипергеометрическое распределение задает вероятность числа…?
В партии из 12 деталей имеется 8 стандартных. Найти вероятность того, что среди 5 взятых наудачу деталей окажется 3 стандартных.
3. Биноминальное распределение при выборочном контроле показывает…?
Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений герба.
4. Распределение Пуассона применяется, когда вероятность…? событий…?
Завод отправил на базу 1000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,02. Найти вероятность того, что на базу прибудут 2 неугодных изделий
5. Нормальное распределение дает хорошую модель для реальных условий:
– ?
– ?
– ?
Назовите их.
6. Как влияет значение математического ожидания на форму графика плотности нормального распределения (х) ?
7. Как влияет значение среднего квадратического отклонения () на форму графика плотности нормального распределения (х)?
8. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (20,50).
9. Что такое размах?
10. Показательное распределение определяется…? параметром оно применяется в задачах…?
Задачи
1.Определить вероятность получения 2-х бракованных изделий в выборке из 20-ти штук, если вероятность брака для процесса составляет 0, 04 (или 4%). Использовать таблицу биноминального распределения.
2.Завод отправил на базу 5000 доброкачественных изделий. Вероятность повреждения изделий внутри равна 0, 0002. Найти вероятность того, что на базу прийдут три негодных изделия (распределение Пуассона).
3. Вероятность установки инструмента равна 0,6. Найти вероятность того, что установка произойдет с 3-его захода ( геометрическое распределение).
4.Из 50 изделий нанесено покрытие на 20-ти. Найти вероятность того, что среди наугад извлеченных 5 изделий окажутся ровно три без покрытия. ( гипергеометрическое распределение).
5. В партии из 10 деталей 8 стандартных. Найти вероятность того, что из наугад извлеченных двух деталей есть хотя бы одна стандартная.
6. В таре находится 10 деталей. Из них 2 нестандартных. Найти вероятность того, что в наугад отобранных 6 деталях окажется не более одной нестандартной.
Погрешности измерений:
1) Что относится к инструментальным погрешностям?
2) Каковы причины инструментальных погрешностей?
3) К каким погрешностям относится погрешности, вызванные изменением внешних условий?
4) Чем обусловлены методические погрешности?
5) Можно ли заранее знать методические погрешности?
6) Что называется систематическими погрешностями?
7) Что является случайной погрешностью?
8) Почему возникают случайные погрешности?
9) Могут ли случайные погрешности быть учтены заранее?
10) Что нужно сделать для учета влияния случайных погрешностей на результат измерения?
В пакете IBM SPSS STATISTICA сгенерировать данные соответствующие заданному закону распределения.
Выявление изменений в качестве
1) В чем заключается сущность анализа улучшений?
2) Всегда ли увеличение среднего после нововведения означает улучшение процесса?
3) Может ли не одна, а несколько альтернативных гипотез?
4) Что такое ошибка первого рода?
5) Что такое ошибка второго рода?
6) Достаточно ли знания среднего и его дисперсии (или ее оценки) для вывода о существенном отклонении среднего?
7) Необходимо ли знать дисперсию (или ее оценку) исходного среднего при оценке изменения среднего?
8) Необходимо ли знать среднее значение случайной величины при оценке изменения дисперсии?
9) Как повлияет количество экспериментальных данных на надежность вывода об изменении среднего?
10) Как повлияет количество экспериментальных данных на надежность вывода об изменении дисперсии?
Тема 4
Применить теорию и построить все шесть инструментов контроля качества.
