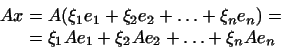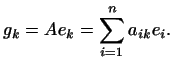11. Умножение матриц. Свойства, примеры.

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

Определение

Пусть даны две прямоугольные матрицы и размерности и соответственно:

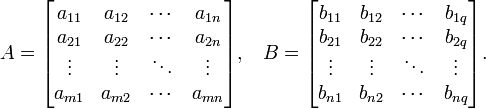
Тогда матрица размерностью называется их произведением:

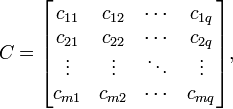
где:

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Следует заметить, что из существования произведения вовсе не следует существование произведения

Свойства

Сочетательное свойство:

Распределительное свойство:

.

Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:

Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:

Если и — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств.

Умножение матриц в целом некоммутативно:

Если , то матрицы и называются перестановочными или коммутирующими между собой.

Определитель и след произведения не зависят от порядка умножения матриц :

12. Запись системы линейных уравнений в матричном виде. Связь между изменением базиса и матрицами. Двойное изменение базиса. Координаты вектора в новом базисе.

В общем случае линейное уравнение имеет вид:

a₁x₁+a₂x₂+...+a_nx_n=b

где:

• a₁, a₂,...,a_n, b — постоянные величины

• x₁, x₂,..., x_n — неизвестные

Любой n-мерный вектор Х = (x₁, x₂,....x_n) называется решением уравнения, если при подстановке его координат уравнение обращается в тождество.

Два линейных уравнения называются равносильными, если они имеют одно и тоже множество решений.

Три случая при решении линейных уравнений

1. Если коэффициенты при неизвестных a₁ = a₂ = ... = a_n =0 и b = 0, в этом случае уравнение имеет вид: 0*x₁+0*x₂+...+0*x_n=0 и называется тривиальным (данное уравнение имеет бесконечное множество решений)

2. Если коэффициенты a₁ = a₂ = ... = a_n =0, а b ≠ 0, в этом случае уравнение имеет вид: 0*x₁+0*x₂+...+0*x_n= b и называется противоречивым. (данное уравнение не имеет ни одного решения)

3. Хотя бы один из коэффициентов при неизвестных отличен от нуля.

Пусть а₁ ≠0. В этом случае можно разрешить уравнение относительно x₁:

Важно: При этом x₁ называется разрешенной неизвестной, x₂, x₃,....,x_n называются свободными неизвестными. Если свободными неизвестным придать любые конкретные значения x₂=k₂, x₃=k₃,...,x_n=k_n, то вектор K=(k₂, k₃,...,k_n) является решением исходного уравнения.

Матричная форма записи

В матричной записи система линейных уравнений может быть записана следующим образом:

AX=B

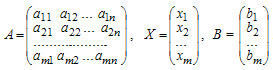
Пример 2: Записать в матричном виде систему из предыдущего примера

Связь между матрицами и линейными преобразованиями.

Пусть -- некоторый базис в -мерном пространстве и -- линейное преобразование в .

Для любых векторов существует одно и только одно линейное преобразование , такое что

Докажем это. Покажем сначала, что преобразование однозначно определяется векторами . Действительно, пусть

(1)

-- произвольный вектор из . Тогда

и, следовательно, однозначно определяется по .

Теперь покажем, что для всяких векторов существует линейное преобразование , такое, что . Для этого поставим в соответствие векторам векторы ; произвольному же вектору поставим в соответствие вектор . Так как вектор выражается через однозначно, то ему ставится в соответствие вполне определенный вектор . Легко проверить, что так определенное преобразование линейно.

Обозначим координаты вектора в базисе через , т.е. положим

(3)

Совокупность чисел ( ) образует матрицу

которую мы назовем матрицей линейного преобразования в базисе .

Итак, мы доказали, что при заданном базисе каждому линейному преобразованию однозначно соответствует матрица , и, обратно, каждой матрице однозначно отвечает линейное преобразование, определяемое формулами (3), (1), (2).

Мы видим, таким образом, что линейные преобразования можно описывать с помощью матриц и матрицы являются тем аналитическим аппаратом, с помощью которого изучаются линейные преобразования в конечномерных пространствах.

Заметим, что при изменении базиса матрица, соответствующая данному линейному преобразованию, вообще говоря, изменится.