
- •Группы, кольца, поля. Определения и примеры. Кольца из 2-5 элементов. Область целостности.
- •Комплексные числа. Определение, нормальная форма. Поле комплексных чисел.
- •Комплексные числа на плоскости. Модуль и аргумент числа, тригонометрическая форма. Сопряженные числа и их свойства.
- •Произведение комплексных чисел в тригонометрической форме. Возведение числа в степень и извлечение корня.
- •7. Векторные пространства. Определение и примеры. Свойства нуля. Линейное выражение.
- •8. Линейно зависимые и линейно независимые системы векторов. Свойства. Порождающие системы векторов. Примеры. Линейно зависимые и линейно независимые системы векторов
- •9. Базис. Теорема о базисе. Количество векторов в базисе. Размерность и ранг. Примеры. Координаты вектора в базисе.
- •10. Матрицы. Определение матрицы. Сложение матриц, умножение матрицы на число и транспонирование матрицы. Их свойства.
- •11. Умножение матриц. Свойства, примеры.
- •Запись системы линейных уравнений в матричном виде. Связь между изменением базиса и матрицами. Двойное изменение базиса. Координаты вектора в новом базисе.
- •Изменение координат вектора при изменении базиса
- •Элементарные преобразования в матричном виде. Теорема о ранге матрицы.
- •Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Свойства ранга матрицы. Связь с обратными матрицами. Теорема Кронекера-Капелли.
- •Свойства
- •Необходимость
- •Достаточность
- •Следствия
- •15. Перестановки. Произведение перестановок. Транспозиция. Перестановка как произведение транспозиций и транспозиция как произведение транспозиций соседних элементов.
- •16. Инверсии в перестановке. Четность перестановки. Связь с транспозициями. Четность произведения перестановок.
- •17. Определение определителя. Определители небольших порядков. Начальные свойства (1-6).
- •18. Дальнейшие свойства. Алгебраическое дополнение и минор. Разложение по строке. Примеры.
- •19. Теорема Крамера. Нахождение обратной матрицы с помощью определителей. Определитель произведения.
- •§2 Свойства умножения матриц
- •20.Определение многочлена от одной переменной. Действия с многочленами и их свойства. Пространство и кольцо многочленов.
- •21. Нормальная форма записи многочленов. Степень многочлена и ее свойства. Кольцо многочленов над областью целостности.
- •22. Значение многочлена в точке. Деление с остатком. Две теоремы о делении с остатком. Схема Горнера.
- •Деление с остатком
- •Теорема Безу
- •23. Теорема Безу. Корень многочлена, количество корней у многочлена. Теорема о тождестве. Алгебраически замкнутые поля, основная теорема алгебры (б/д). Разложение на линейные сомножители.
- •24. Решение уравнений третьей степени.
- •25.Решение уравнений четвертой степени.
- •27. Взаимно простые многочлены. Определение, свойства
- •29. Неприводимые многочлены над полями комплексных и вещественных чисел.
- •31. Многочлены от нескольких переменных. Симметрические многочлены. Теорема о симметрических многочленах.
10. Матрицы. Определение матрицы. Сложение матриц, умножение матрицы на число и транспонирование матрицы. Их свойства.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Матрицы допускают следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую строк);
умножение матрицы на элемент основного кольца или поля (т. е. скаляр).
Операции над матрицами
Умножение матрицы на число
Умножение матрицы
на
число
![]() (обозначение:
(обозначение:
![]() )
заключается в построении матрицы
)
заключается в построении матрицы
![]() ,
элементы которой получены путём умножения
каждого элемента матрицы
на
это число, то есть каждый элемент матрицы
равен
,
элементы которой получены путём умножения
каждого элемента матрицы
на
это число, то есть каждый элемент матрицы
равен
![]()
Свойства умножения матриц на число
1. 1*A = A;
2. (Λβ)A = Λ(βA)
3. (Λ+β)A = ΛA + βA
4. Λ(A+B) = ΛA + ΛB
Сложение матриц
Сложение матриц
![]() есть
операция нахождения матрицы
,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц
и
,
то есть каждый элемент матрицы
равен
есть
операция нахождения матрицы
,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц
и
,
то есть каждый элемент матрицы
равен
![]()
Свойства сложения матриц
5.коммутативность;
6.ассоциативность;
7.сложение с нулевой матрицей;
8.существование противоположной матрицы;
Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:
Множество всех матриц одинаковых размеров MxN образуют линейное пространство над полем P (полем всех действительных или комплексных чисел), поэтому каждая матрица является и вектором этого пространства.
Умножение матриц
Умножение
матриц (обозначение:
![]() ,
реже со знаком умножения
,
реже со знаком умножения
![]() )
— есть операция вычисления матрицы
,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
)
— есть операция вычисления матрицы
,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
Количество столбцов в матрице
должно
совпадать с количеством строк в матрице
.
Если матрица
имеет
размерность
![]() ,
—
,
—
![]() ,
то размерность их произведения
,
то размерность их произведения
![]() есть
есть
![]() .
.
Свойства умножения матриц
1.ассоциативность;
2.произведение не коммутативно;
3.произведение коммутативно в случае умножения с единичной матрицей;
4.справедливость дистрибутивного закона;
5.(ΛA)B = Λ(AB) = A(ΛB);
Комплексное сопряжение
Если элементами матрицы
![]() являются
комплексные числа, то комплексно
сопряжённая (не путать с эрмитово
сопряжённой! см. далее)
матрица равна
являются
комплексные числа, то комплексно
сопряжённая (не путать с эрмитово
сопряжённой! см. далее)
матрица равна
![]() .
Здесь
.
Здесь
![]() —
число, комплексно
сопряжённое к
—
число, комплексно
сопряжённое к
![]() .
.
Транспонирование и эрмитово сопряжение
Транспонирование
уже обсуждалось выше: если
,
то
![]() .
Для комплексных матриц более употребительно
эрмитово сопряжение:
.
Для комплексных матриц более употребительно
эрмитово сопряжение:
![]() .
С точки зрения операторного взгляда на
матрицы, транспонированная и эрмитово
сопряжённая матрица — это матрицы
оператора, сопряжённого
относительно скалярного
или эрмитова
произведения, соответственно.
.
С точки зрения операторного взгляда на
матрицы, транспонированная и эрмитово
сопряжённая матрица — это матрицы
оператора, сопряжённого
относительно скалярного
или эрмитова
произведения, соответственно.
Транспонированная матрица — матрица
![]() ,
полученная из исходной матрицы
заменой
строк на столбцы.
,
полученная из исходной матрицы
заменой
строк на столбцы.
Формально, транспонированная матрица
для матрицы
размеров
—
матрица
размеров
![]() ,
определённая как AT[i, j]
= A[j, i].
,
определённая как AT[i, j]
= A[j, i].
Например,
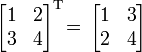 и
и

Свойства транспонированных матриц
Дважды транспонированная матрица А равна исходной матрице А.
Транспонированная сумма матриц равна сумме транспонированных матриц.
Транспонированное произведение матриц равно произведению транспонированных матриц
При транспонировании можно выносить скаляр.
Определитель транспонированной матрицы равен определителю исходной матрицы.
