
- •3. Схема уровней и основные серии спектра атомов(ионов) с одним валентным электроном (на примере к 19).
- •4. Схема уровней и основные серии спектра атомов(ионов) с двумя валентными электронами (одноэлектронное возбуждение на примере Hg)
- •8. Энергетич. Состояния е-ов в Ме. Зонная схема Ме и их физ-ие св-ва.
- •10. Эффект Шоттки. Автоэлектронная, вторичная и фотоэмиссии электронов. Области применения.
- •13.Классификация электрических токов в газе….
- •14. Пробой газа при высоком давлении. Закономерности формирования токопроводящего канала.
- •15. Тлеющий разряд. Элементарные процессы и продольное распределение параметров в тлеющем разряде.
- •17.Излучение неизотермической плазмы тлеющего и дугового разрядов. Процессы, определяющие спектральный состав излучения и его зависимость от давления
- •19.Самостоятельный дуговой разряд (низких, средних и высоких давлений).
- •20.Баланс энергии в самостоятельном разряде.
- •24.Преобразование энергии возбуждения в диэлектриках и полупроводниках. Энергетический выход люминесценции.
- •25. Полупроводниковые лазеры с электронной накачкой. Принцип действия и параметры.
- •26.Свойства контакта Ме – п/п.
- •27. Свойства контакта “полупроводник-полупроводник”. Гомо- и гетероструктуры.
- •28.Условие усиления излучения для межзонных переходов. Принцип действия сд и инжекционных лазеров
- •2. Основные положения векторной модели атома. Природа возникновения тонкой структуры атомных термов. Схемы сложения моментов.
- •7. Классификация взаимодействий частиц в газе. Следствия из законов сохранения энергии и импульса при парных столкновениях. Упругие и неупругие столкновения
- •11. Диффузия и дрейф заряженных частиц. Соотношение Эйнштейна.
- •9. Виды эмиссии электронов. Термоэлектронная эмиссия. Закон Ричардсона - Дешмена.
- •23.Основные виды оптического поглощения твердых тел. (Полупроводники и диэлектрики)
- •6 . Природа расщепления спектральных линий атомов в магнитном поле.
- •16. Самостоятельный дуговой разряд низкого и высокого давлений. Распределение параметров и элементарные процессы в разряде.
1 Моемнт кол-ва движ. и магнит. момент атома.
В![]() квантовой механике система, в частности
атом, может быть одновременно
охарактеризована определёнными
значениями энергии Е, квадрата момента
количества движения Mλ2
и одной из его
проекций, например,MλZ.Собственные
функции и собственные значения квадрата
момента количества движения для атома
определяются уравнением
квантовой механике система, в частности
атом, может быть одновременно
охарактеризована определёнными
значениями энергии Е, квадрата момента
количества движения Mλ2
и одной из его
проекций, например,MλZ.Собственные
функции и собственные значения квадрата
момента количества движения для атома
определяются уравнением
П![]()
![]() одставляя
значение оператора
Mλ2
в сферических
координатах, получаем уравнение, которое
имеет определённое решение при условии,
что λ принимает значения λ
= λ (λ +1)η2,
где λ - целое число. Следовательно,
собственные значения квадрата момента
количества движения равны: Mλ2=
λ (λ +1)η2,
(2) откуда для численного значения момента
количества движения находим Mλ=
η(λ (λ +1)0,5
(λ =
0,1,2…). (3)
одставляя
значение оператора
Mλ2
в сферических
координатах, получаем уравнение, которое
имеет определённое решение при условии,
что λ принимает значения λ
= λ (λ +1)η2,
где λ - целое число. Следовательно,
собственные значения квадрата момента
количества движения равны: Mλ2=
λ (λ +1)η2,
(2) откуда для численного значения момента
количества движения находим Mλ=
η(λ (λ +1)0,5
(λ =
0,1,2…). (3)
(далее квантовое число m будем использовать с индексом ml ).Собственные функции и собственные значения проекции момента количества движения на преимущественное направление (ось Z) определяются в соответствии с видом оператора MλZ уравнением:
Р![]() ешение
этого уравнения с точностью до постоянного
множителя имеет вид:
ешение
этого уравнения с точностью до постоянного
множителя имеет вид:
![]() Требование
однозначности
решения приводит к следствию, что λ
ג
может
принимать лишь значения
λ = ml∙ħ, где ml = 0, ±1, ±2…±ℓ
.( ml
квантовое число). Отсюда получаем, что
проекция момента количества движения
может принимать лишь одно из следующих
значений: MλZ
=mλ
η (ml = 0, ±1, ±2….±ℓ). (5)
В соответствии с (5) и (3), численные
значения МL
и МLZ
в квантовой механике никогда не совпадают,
в то время как в классической теории
Бора МLZ
может принимать значения ±
МL.
На рис.1
изображено модельное представление
момента количества движения МL
и его проекции МLZ
для орбитального квантового числа ℓ
.Из уравнения Шрёдингера:
Требование
однозначности
решения приводит к следствию, что λ
ג
может
принимать лишь значения
λ = ml∙ħ, где ml = 0, ±1, ±2…±ℓ
.( ml
квантовое число). Отсюда получаем, что
проекция момента количества движения
может принимать лишь одно из следующих
значений: MλZ
=mλ
η (ml = 0, ±1, ±2….±ℓ). (5)
В соответствии с (5) и (3), численные
значения МL
и МLZ
в квантовой механике никогда не совпадают,
в то время как в классической теории
Бора МLZ
может принимать значения ±
МL.
На рис.1
изображено модельное представление
момента количества движения МL
и его проекции МLZ
для орбитального квантового числа ℓ
.Из уравнения Шрёдингера:
П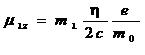 оскольку
решение общего урав-я Шрёдингера есть
фун-я координат и времени, то можно
вычислить заряд, переносимый в единицу
времени через ед-цу площади, т.е. плотность
электрического тока. Магнитный момент,
соответствующий круговому току,
определяется как:
оскольку
решение общего урав-я Шрёдингера есть
фун-я координат и времени, то можно
вычислить заряд, переносимый в единицу
времени через ед-цу площади, т.е. плотность
электрического тока. Магнитный момент,
соответствующий круговому току,
определяется как:
При заданном механическом моменте величина магнитного момента для различных систем и для различных состояний рассматриваемой системы, вообще говоря, различна. Поэтому важной характеристикой магнитного момента является отношение его величины к величине соответствующего механического момента, т.н. гиромагнитное отношение γ.
(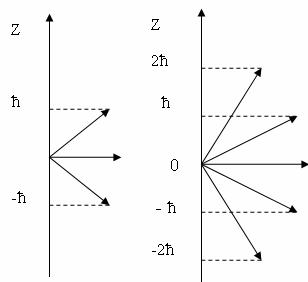 Рис.1
Орбитальный момент количества движения
Рис.1
Орбитальный момент количества движения
и его проекции на преимущественное направление для атома водорода.)
В этом отношении находятся величины моментов и величины их проекций
Поскольку МLZ= ћml, то из (6) для орбитальных моментов γ=e/2m0c,(8)величина магнитного орбитального момента μλ= e/2m0c
Магнитный момент атома не определяется только орбитальным движением электронов. Уэлектрона собственный механический и магнитный моменты. Собственный механический момент электрона Ms называют также спиновым или просто спином. Величина спинового момента численно равна MS= η(s(s+1))0.5,(10) где s = 1 / 2 , а проекция спинового момента электрона на преимущественное направление может принимать лишь два следующих значения: MS.Z=mS η, mS=+_0.5 (11)
Гиромагнитное отношение для собственных моментов вдвое больше чем для орб-ых моментов.μS=eMS/m0c.Наличие орбитального и собственного магнитных моментов приводит к их взаимодействию, которое называется спин – орбитальным. Спин – орби-ное вз-ие для атомов, как правило, значительно меньше электростатического и его можно представить как взаимодействие соответствующих мом-ов кол-ва движения и, как следствие, состояние должно определяться полным механическим моментом. Полный момент количества движения атома Mj, с точки зрения механической модели определяется векторным сложением орбитального и спинового моментов. Вводится понятие оператора квадрата полного механ-го момента и доказывается, что квадраты орбитального момента Mλ2, спинового мом-та MS2 и полного мом-та электрона MJ2 в атоме являются величинами, одновременно определимыми.
3. Схема уровней и основные серии спектра атомов(ионов) с одним валентным электроном (на примере к 19).
19К : 1s22s22p63s23p64s1
4s1=> n=4 , l=0 => L=0
s=1/2 => S=1/2 2s+1=2
основной терм: 42S1\2
составим таблицу:
n |
l |
j |
терм |
4 |
0 |
1/2 |
2S1\2 |
4 |
1 |
3/2 |
2P3\2 |
4 |
1 |
1/2 |
2P1\2 |
4 |
2 |
5/2 |
2D5\2 |
4 |
2 |
3/2 |
2D3\2 |
4 |
3 |
7/2 |
2F7\2 |
4 |
3 |
5/2 |
2F5\2 |
n |
l |
j |
терм |
5 |
0 |
1/2 |
2S1\2 |
5 |
1 |
3/2 |
2P3\2 |
5 |
1 |
½ |
2P1\2 |
5 |
2 |
5/2 |
2D5\2 |
5 |
2 |
3/2 |
2D3\2 |
5 |
3 |
7/2 |
2F7\2 |
5 |
3 |
5/2 |
2F5\2 |
5 |
4 |
9/2 |
2G9\2 |
5 |
4 |
7/2 |
2G7\2 |
n=4 , l=3 => L=3
J=7/2, 5/2
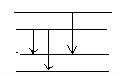
Главная серия спектра (переход из возбужденных Р термов на оси S терм)
ν1=4S1\2-n2P1\2
ν1=4S1\2-n2P3\2 n=4,5,6
2-ая побочная серия ( переход с возбужд. S –термов на первые возбужд. Р термы)
ν1=42P1\2-n2S1\2
ν1=42P1\2-n2S3\2 n=5,6
Δ ν -расстояние м/у линиями=const, а расстояние м/у 2-ми линиями (ν гр-второй потенциал ионизации)
1-ая побочная серия (переход между P4D термами)
ν1=42P1\2-n2D3\2 ΔJ=1
ν1=42P3\2-n2D3\2ΔJ=0 n=4,5
ν1=42P3\2-n2D5\2ΔJ=1
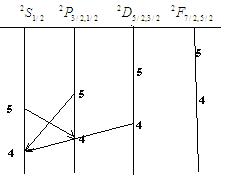
4. Схема уровней и основные серии спектра атомов(ионов) с двумя валентными электронами (одноэлектронное возбуждение на примере Hg)
4f145d106s2
Собст. значения e |
L |
Синглет. термы |
Триплетные термы |
||||||
1 |
2 |
J |
терм |
J |
терм |
||||
6S |
7S |
0 |
0 |
1S0 |
1 |
3S1 |
|||
S |
P |
1 |
1 |
1P1 |
2,1,0 |
3P2,1,0 |
|||
S |
D |
2 |
2 |
1D2 |
3,2,1 |
3D3,2,1 |
|||
S |
F |
3 |
3 |
1F3 |
4,3,2 |
3F4,3,2 |
|||
|
|
||||||||
Главная серия:
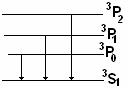
ν1=63S1-63P0
ν2=63S1-63P1
ν3=63S1-63P2
Соотношение интенсивностей между линиями будет определяться соотношение статистических весов P-термов
2 Побочная серия:
ν1=63P0-73S1
ν2=63P1-73S1
ν3=63P2-73S1
1 Побочная серия:
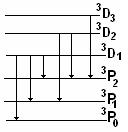
ν1=63P0-63D1
ν2=63P1-63D1
ν3=63P2-63D1
ν4=63P1-63D2
ν5=63P2-63D2
ν6=63P2-63D3
5.Схема уровней и основные серии спектра атомов (ионов) с двумя валентными электронами ( на примере Са 20).
Состояния электроновс |
L |
Синглетные термы |
Триплетные термы |
|||
У |
терм |
J |
Терм |
|||
1 |
2 |
|||||
n1S |
n2S |
0 |
0 |
1S0 |
1 |
3S1 |
S |
P |
1 |
1 |
1P1 |
2,1,0 |
3S2 3P1 3P0 |
S |
d |
2 |
2 |
1D2 |
3,2,1 |
3D3 3D2 3D1 |
S |
f |
3 |
3 |
1F3 |
4,3,2 |
3F4 3F3 3F2 |
l1=l2=0, L=0, S=0, J=0
n1≠n2 S=1, 2S+1=3, J=1
l1=0, l2=1, L=1 для синг. термов S=0 => J=1 => 1P1
для триплетных S=1, L=1, J=2,1,0
l1= 0, l2=2 L=0, S=0, J=2
S=1 J=3,2,1
l1=0, l2=3, L=3, S=0, J=3
S=1 J=4,3,2 J=|L+S|…|L-S|
Первая синглетная схема состояний из линий обусловленных пересечением из 1P1 и 1S0: V1=n1S0- n1P1
Вторая синглетная схема из более высоких S состояний на 1P1: V2= n1P1- n1D2
В общем случае можно рассматривать ситуацию когда есть 3S1 терм:
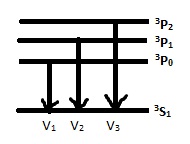
V1= n3S1- n3P0
V2= n3S1- n3P1
V3= n3S1- n3P2
Соотношение интенсивностей м/у линиями будет определяться соотношением статистических весов р-термов: JV1:JV2:JV3:=1:3:5;
Зазор между частотами в каждой тройке линий будет сокращаться.
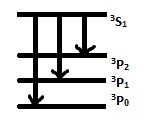
V1= n3P0- (n+1)3S1
V2= n3P1- (n+1)3S1
V3= n3P2- (n+1)3S1
Комбинация D и P термов:
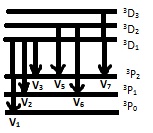
V1= n3P0- n3D1
V2= n3P1- n3D1
V3= n3P2- n3D1
V1= n3P1- n3D2
V2= n3P2- n3D2
V3= n3P2- n3D3
![]()
