Тема 2. Модели отказов.

Различные виды и степень повреждения материала влияют на выходные параметры изделия и, следовательно, определяют его надёжность. Основная задача теории надёжности состоит в выявлении и математическом описании функциональной зависимости выходного параметра x(t) от частоты и степени повреждения U(t).

Поскольку частота и степень повреждения отдельных деталей машины являются величинами случайными, то математические описания закономерностей опираются на теорию вероятности. Теория вероятностей даёт широкий ассортимент различных законов распределения случайных величин, которые могут быть использованы для решения задач надёжности.

Из практики исследования надёжности оборудования установлено, что отказы машин и аппаратов подчиняются следующим распределениям вероятности: равномерному, нормальному, логарифмически - нормальному, экспоненциальному, Релея, Вейбулла, гамма распределению и др. Под математической моделью отказов оборудования и его элементов понимается закон распределения вероятности случайной величины - отказа.

Закон распределения времени работы изделия до отказа в дифференциальной форме в виде плотности вероятности f(t) или в интегральной форме в виде функции распределения F(t) является полной характеристикой надёжности изделия или его элемента. Он позволяет определить вероятность безотказной работы P(t) =1-F(t), математическое ожидание (средний срок службы или средняя наработка до отказа)

Дисперсию D или среднее квадратичное отклонение

и другие численные характеристики.

Основная задача теории надёжности состоит в выявлении и математическом описании такого закона распределения f(t), который отражал бы с высокой степенью достоверности объективную действительность. Это необходимо для возможности прогнозирования поведения изделия с точки зрения оценки вероятности возникновения отказа. Т.е. математические модели надёжности, используемые на практике, представляют простые законы распределения, выражаемые элементарными функциями или интегралами от этих функций.

Показатели надёжности при этом являются некоторыми функциями математической модели и их определение, как правило включает три этапа:

1. Установление типа модели ( закона распределения );

2. Оценка параметров распределения;

3. Определение показателей надёжности на основании модели (закона распределения)

При построении моделей и определении параметров надёжности используют опытные данные или же физико-статистическую теорию.

Распределения, применяемые в качестве моделей надёжности бывают дискретными и непрерывными.

Законом распределения дискретной случайной величины называется совокупность пар чисел (x_i, P_i) ,где x_i - возможные значения случайной величины, a P_i - вероятности, с которыми она принимает эти значения. При этом , i€1.

Распределение случайной величины ζ, называется непрерывным, если существует такая интегрируемая функция Р_ζ(х), - ∞ <х<∞, что в любой точке х .

Функция Р_ζ(х), - ∞ <х<∞ называется плотностью вероятности случайной величины или плотностью распределения F_ζ(x).

В таблице 5 приведены законы распределения, получившие наибольшее применение в теории надёжности.

В таблице 5 t - наработка до отказа, случайная дискретная величина; а - среднее квадратичное отклонение; Т_ср - средняя наработка до отказа; λ, м - параметры модели; Ф - нормированная функция Лапласа.

2.1. Выбор закона распределения.

В теории надёжности нормальное распределение используется чаще всего для описания случайных величин, связанных со старением конструктивных элементов машин и аппаратов - т.е. используется для математического описания вероятностных законов различных видов изнашивания, коррозии, эрозии и т.д., для описания разброса числовых значений разнообразных свойств конструкционных материалов, деталей, узлов, устройств. Такое распределение имеет место, когда на изделие воздействует совместно большое число разнообразных, но не значительных факторов, каждый из которых сам по себе вызывает лишь незначительное воздействие по сравнению со всей совокупностью. Нормальный закон распределения аппроксимирует законы распределения плотности отказов с приемлемой инженерной точностью, если коэффициент вариации этого закона меньше значений 0,33.

Плотность вероятности нормального распределения находится по уравнению

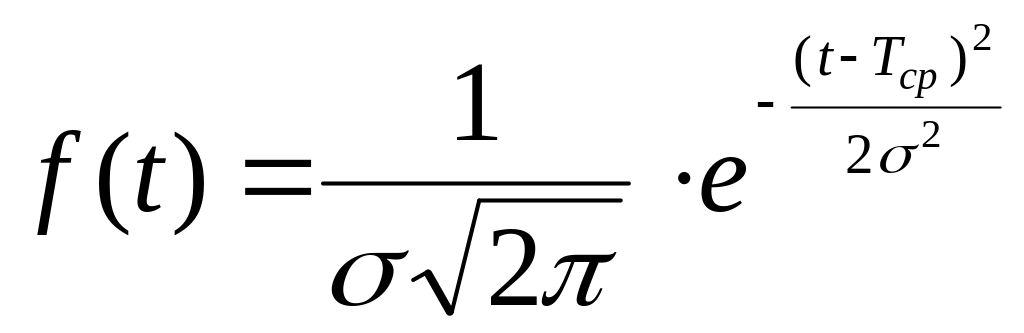
Функция распределения

где - нормированная функция Лапласа.

P(t)=l-F(t)

Вероятность безотказной работы определяют как

Среднее квадратичное отклонение при этом определяют как , где D- дисперсия.

Где n_i -число отказов, приходящее на i- интервал, середина которого t_i;

N_o - число отказов за рассмотренное время.

Логарифмически - нормальным законом распределения обычно аппроксимируются такие отказы, которые образуются в результате перемножения большого числа независимых или даже слабо зависимых величин, причём дисперсия каждой из этих величин мала в сравнении с дисперсией их суммы. Это в сравнение используется для математического описания таких отказов, которые развиваются под влиянием незначительных воздействий, но эффект от каждого такого воздействия пропорционален мгновенному значению случайной величины. Подобное явление имеют место, например при разрушении, дроблении.

Аппроксимация - замена одних математических объектов (чисел или функций) другими, более простыми в том или ином смысле близкими к исходным.

Плотность вероятности распределения отказов рассчитывается по формуле:

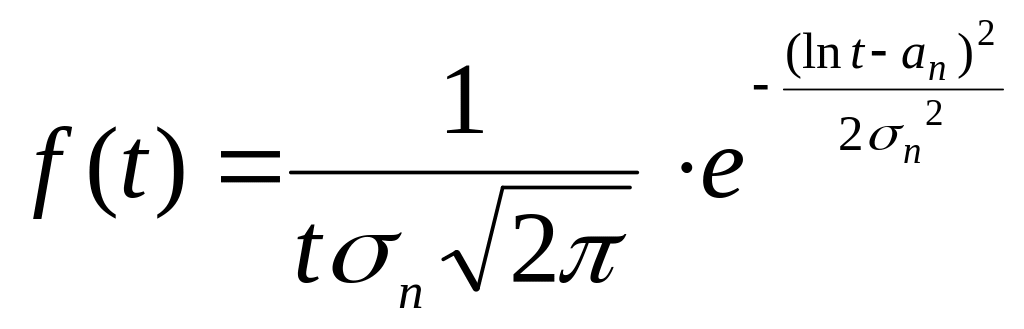
где a_n и σ_n - параметры распределения.

- средняя наработка до отказа.

Дисперсию определяют как :

D = σ² = ехр (2a_n +σ_n²/2)( е^σn2 - 1)

Параметры распределения а_п и σ_n определяются по формулам:

где t_i - наработка на отказ;

n — общее число отказов

Причины возникновения внезапных отказов не связана с изменением состояния изделия и временем его предыдущей работы, а зависит от уровня внешних воздействий. Поэтому при построении модели внезапного отказа надо охарактеризовать ту обстановку, те внешние условия, которые могут привести к отказу. Эта обстановка может оцениваться интенсивностью отказов λ-вероятностью возникновения отказа в единицу времени при условии, что до этого момента времени отказ не возник. Поэтому λ является условной плотностью вероятности и измеряется в тех же величинах, что плотность вероятности f(t), т.е. [1/ч].

Показатель интенсивности отказов λ широко используется в технике, особенно в радиоэлектронике, где значительно больший объём отказов относится к категории внезапных.

Применение λ - характеристики удобно в том случае, если она не изменяется во времени и характеризует условия возможного возникновения отказа.

Принимая λ — const получим экспоненциальный закон надёжноcти

(1)

Плотность вероятности данного закона с учётом

; (2)

Средний срок службы (наработка) до отказа для экспоненциального закона будет:

, и формула (1) может быть написана в следующем виде:

Дисперсия (D) (3)

Для современных деталей и узлов машин требуется, как правило, высокая вероятность безотказной работы от P(t) = 0,99 до P(t) = 0,99999 и выше.

Для значений P(t) > 0,9 формулу (3) можно с достаточной для практики точностью представить в следующем виде:

P(t) = 1-λt = 1-t/T_cp (4)

Следует отметить, что при значениях P(t) близких к единице, условие λ=const, что видно из формулы, т.к. в этом случае λ(t)≈f(t). Одно из отличий характеристики λ(t) от f(t) заключается в том, что при t →∞ всегда f(t)→0, в то время как для λ этого не обязательно.

При применении экспоненциального закона обычно указывают, что условие λ=const сохраняется лишь в течении некоторого периода времени. Типичная кривая λ(t) показана на рисунке 1, где начальный период (0, t_р) характеризуется повышением интенсивности отказов. Это связывают с приработкой изделия, когда проявляются технологические дефекты. Второй период (t₁ , t₁) когда λ=const, называют периодом нормальной эксплуатации, после чего (при t >t₂) начинается появляться износ.

λ

t₁

t₂

t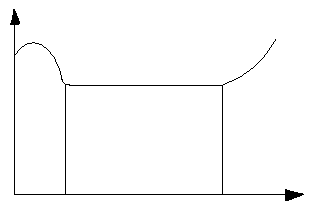

Рисунок 1.- Кривая интенсивности отказов.

Здесь напомним, что рассматриваются внезапные отказы, не связанные с процессом старения изделий.

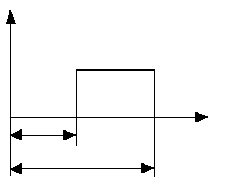
Равномерное распределение отказов может иметь место для отдельных элементов машин и аппаратов. Оно характеризуется тем, что плотность распределения отказов остаётся величиной постоянной на отрезке времени от Т₁ до Т₂. Плотность распределения рассчитывается

вероятность безотказной работы

Т₂-Т₁, гдеТ₁<1<Т₂.

Т₁ ,Т₂ - отрезок времени, на котором рассматривается работа машины или аппарата.

Закон нормального распределения наиболее часто встречается в природе, а закон Вейбулла – охватывает практически все явления, т. к. при м=1 – экспоненциальный закон, при м>1 близок к нормальному, при м=2 распределение Релея.

Закон Вейбула

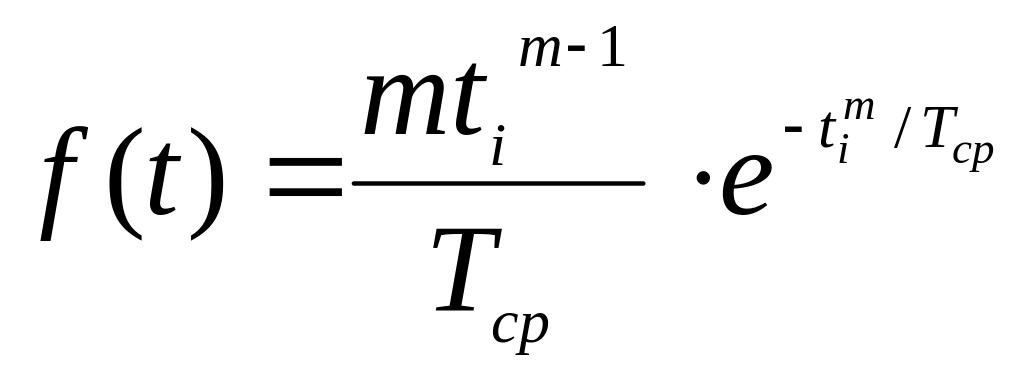
Закон распределения Релея

P(t)

f(t)

1,0

Выбор модели отказов сводится к выбору распределения, которому подчиняется случайная величина — отказ. Расчёт выполняют в следующем порядке. В начале по известным экспериментальным значениям времени безотказной работы аппаратов строят экспериментальные кривые плотности распределения отказов f(t)

И вероятности безотказной работы

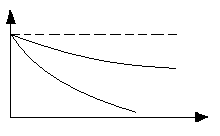
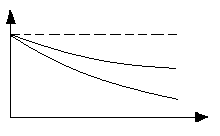
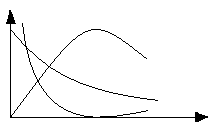
Таблица 2.1 - Законы распределения сроков службы и вероятности безотказной работы.

Закон	f(t)	P(t)
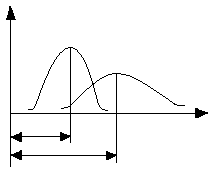
Нормальный (Гаусса)	σ1< σ2 1 2	0,5 1 2 F(t)
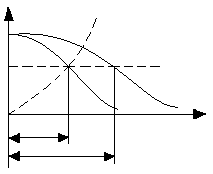
Логарифмический нормальный	σ1=0,1 σ2=0,5
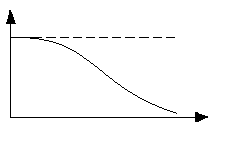
Экспоненциальный	1 λ λ2 2 λ1< λ2	1 2
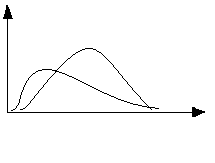
Вейбулла	m>1 m=1 m<1	m=1 m<1 m>1
Равномерное распределение Т2-Т1, гдеТ1<1<Т2.	T1 T2 1	T1 T2

В зависимости от характера работы узлов аппарата выбирают вид распределения и затем рассчитывают теоретические значения параметров распределения: f(t), P(t), F(t). Далее вычисляют разности между теоретическими и экспериментальными значениями P(t) на каждой середине промежутка t_i из полученных разностей выбирают наибольшую абсолютную величину

Правильность выбранного закона распределения оценивается по критерию согласия Колмагорова λ

λ

λ

λ

^* или

,

где К - общее число наработок на отказ.

Если λ^* < 1,0, то считается, что принятый закон распределения адекватно описывает фактическое распределение плотности вероятности отказов.

Если λ^*>1,0, то следует выбрать другой закон распределения.

2.2. Система сбора и анализа эксплуатационных данных по отказам.

Сведения о типичных отказах изделий, полученные на основании сбора и обработки, данных эксплуатации большого числа наблюдений, дают достоверную информацию о действительной работоспособности изделия. Хотя эта информация и относится к уже эксплуатируемым изделиям, она может эффективно использоваться для модернизации и создания, новых образцов. В машиностроении разработана система стандартов, которые регламентируют порядок сбора и учёта информации (ГОСТ 20857-75), формы учёта и методы оценки эксплуатационной информации о надёжности изделий (ГОСТ 19490 -74), способы статистической обработки информации (ГОСТ 17509-72) и др.

На практике обычно используются сведения о работоспособности в процессе эксплуатации и ремонта изделий.

При этом в большей части проводят так называемый пассивный эксперимент. Сущность его заключается в том, что для оценки показателей надёжности используются сведения первичных и сводных хронокарт, технологических и отчётных документов по эксплуатации и ремонту.

Если эксплуатационные наблюдения или исследования позволили получить закон распределения времени безотказной работы данного изделия, то определение параметров безотказности не представляет трудности.

Для этого на основе полученной информации об отказах изделия за период его эксплуатации строится гистограмма, показывающая число возникших отказов в данном интервале времени для большого числа однотипных изделий. По полученной гистограмме, которая является экспериментальной оценкой плотности вероятности, может быть подобран теоретический закон распределения.

Для проверки соответствия экспериментальных данных и высказанной гипотезе о теоретическом распределении в математической статистике разработаны специальные критерии согласия, например, критерий хи-квадрат Пирсона, критерий Колмагорова и др. (Определение законов распределения случайных величин на основе опытных данных см.ниже.).

Результаты эксплуатационных исследований нужны, главным образом, для внесения исправлений в слабые места конструкции, но не для суждения о надёжности выпускаемых машин.

В связи с этим проводятся ускоренные испытания на безотказность, проводимые по плану активного эксперимента. В данном случае подвергается ускоренному испытанию опытный образец. Однако всякое форсированное испытание искажает реальную картину потери работоспособности изделия, поэтому обычно получают только лишь приближённые сведения.

В заключение отметим, что совокупность пассивного и активного экспериментов позволяют с определённой степенью достоверности использовать эти сведения уже на стадии проектирования. (см . Модели отказов.)

2.3. Классификация отказов.

Все отказы можно классифицировать по характеру возникновения и протекания процессов, приводящих к отказу. Дадим определение основным видам отказов и укажем основные причины, приходя­щих к ним.

Постепенные отказы - медленное изменение начального пара­метра изделия. В большей части такой отказ возникает в результате физического износа, коррозии, усталости, ползучести.

Внезапные отказы - резкое изменение параметров изделия. Причинами таких отказов может служить усталостная поломка дета­лей, деформация из-за перегрузок, выход из строя подшипника вследствие прекращения смазки и др.

Отказы функционирования - изделие не может выполнять свои функции. Например, в результате поломки муфты насоса не вращает­ся и насос не выполняет своих функций.

Отказы параметрические - отказ приводит к выходу параметров (характеристик) за допустимые пределы. Например, в результате осмоления насадки из колец Рашига продуктами переработки, экстрак­ционная колонна не обеспечивает проектную производительность.

Допустимые отказы - отказы, находящиеся в пределах, указан­ных в технических условиях на эксплуатацию. Допустимые отказы связаны с процессами старения, которые приводят к постепенному ухудшению выходных параметров изделия.

Например, в сальниковых уплотнениях допускаются небольшие утечки уплотняемой жидкости.

Недопустимые отказы - отказы, связанные с нарушением усло­вий производства и эксплуатации. Например, повышение режимов работы изделия выше допустимых, вращение рабочего колеса в про­тивоположном направлении в виду неправильного подключения кон­тактов к электродвигателю.