Вставка элемента в бинарное дерево поиска
Вставить новую вершину в бинарное дерево поиска довольно просто. С помощью алгоритма поиска, изложенного ранее, отыскивается вершина с одной или двумя нулевыми ссылками left или (и) right. Если ключ вставляемого элемента меньше ключа вершины с нулевой ссылкой left, то эта ссылка направляется к новой вершине, если больше, то к новой вершине направляется ссылка right, если она была нулевой. В результате вставленный элемент оказывается листом (его обе ссылки left и right являются нулевыми). На рисунке 13.2 показан результат вставки в дерево бинарного поиска вершины с ключом 13.
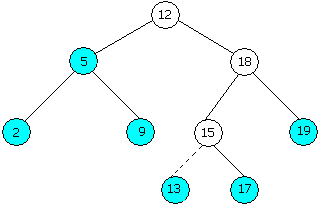
Рисунок 13.2 – Вставка в дерево бинарного поиска элемента с ключом 13. Светлые вершины располагаются на пути от корня к позиции вставки;
пунктиром указана связь, добавляемая при вставке новой вершины
Алгоритм вставки сопряжен с одной проблемой. Хотя алгоритм гарантирует создание допустимого дерева бинарного поиска, после выполнения алгоритма дерево может быть неоптимальным или неэффективным. Пусть в пустое дерево бинарного поиска вставляются элементы с ключами 2, 5, 7, 8. С ключом 2 все просто – он становится ключом корня. Вершины с остальными ключами добавляются в качестве правых дочерних вершин для предшествующих ключей. Результат представляет длинное вытянутое вырожденное дерево, показанное на рисунке 13.3.
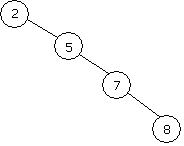
Рисунок 13.3 – Вырожденное дерево бинарного поиска
Если бы можно было гарантировать случайный порядок вставки ключей и вершин, или если бы общее количество вершин было очень небольшим, описанный алгоритм вставки оказался бы приемлемым. Однако в общем случае подобную гарантию нельзя дать, поэтому необходимо использовать более сложный метод вставки, частью которого является стремление сбалансировать дерево бинарного поиска. Этот метод балансировки используется в красно-черных деревьях.
Удаление из бинарного дерева поиска
Процедура удаления заданной вершины z из бинарного дерева поиска рассматривает три возможные ситуации. Если у удаляемой вершины нет дочерних вершин, т. е. удаляемая вершина – лист, то у его родителя указатель на z получает значение Nil.
Если у удаляемой вершины z только одна дочерняя вершина, то с помощью «переброски» указателя от родителя вершины z к ее дочерней вершине, как это показано на рисунке 13.4.
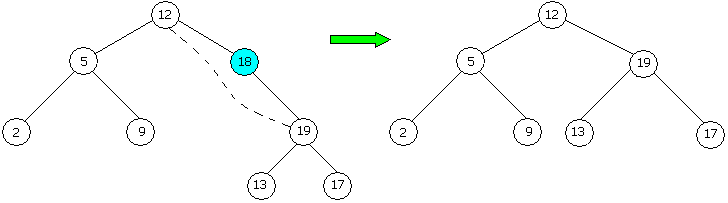
Рисунок 13.4 – Удаление из дерева бинарного поиска элемента с ключом 18, который имеет только одну дочернюю вершину. Двойная стрелка указывает на результат выполнения удаления
Если у удаляемой вершины z имеется две дочерних вершины, то определяется следующая за ним вершина s, у которой нет левого сына. Затем все данные, кроме структурных ссылок, из вершины s копируются в поля удаляемого элемента, а вершина s удаляется путем создания новой связи между ее родителем и сыном. Эти преобразования иллюстрируются рисунком 13.5.
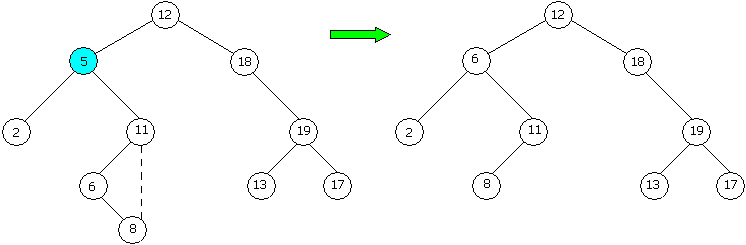
Рисунок 13.5 – Удаление из дерева бинарного поиска элемента с ключом 5, который имеет две дочерних вершины. Вершина 6 удаляется, ее данные копируются в слот вершины 5.
В литературных источниках показано, что бинарные деревья поиска высоты h обеспечивают выполнение базовых операций за время О(h). К базовым операциям в данном случае относятся операции поиска, вставки, удаления, определения максимального и минимального ключа и некоторые другие операции
Таким образом, операции выполняются тем быстрее, чем меньше высота дерева. Однако в наихудшем случае, когда при плохом расположении ключей вставляемых вершин дерево приближается к вырождению, эффективность бинарного дерева поиска ничуть не лучше, чем эффективность, которую обеспечивает линейный связный список.