Поисковые деревья
Бинарное дерево поиска
Структура бинарного дерева поиска и алгоритм поиска
В подразделе 10.7 бинарное дерево поиска представлено как структура, используемая в одном из возможных методов поиска. Перейдем к более детальному рассмотрению подобных деревьев.
Как следует из названия, бинарное дерево поиска (binary search tree) в первую очередь является бинарным деревом, как показано на рисунке 10.3. Такое дерево может быть представлено связанной структурой данных (естественное представление дерева, см. п. 9.4.1), в которой каждая вершина является записью. В дополнение к полю (или полям) ключа key и сопутствующих данных, каждая вершина содержит поля left, right и parent, которые являются указателями на левую и правую дочерние вершины и на родительскую вершину соответственно. Если дочерняя или родительская вершины отсутствуют, то соответствующее поле содержит значение Nil. Единственная вершина, у которой указатель parent равен Nil, – это корень дерева. Ключи в бинарном дереве хранятся в упорядоченном виде: для каждой текущей вершины ключ левой дочерней вершины меньше или равен ключу самой текущей вершины, а этот ключ, в свою очередь, меньше или равен ключу правой дочерней вершины.
Свойство бинарного дерева поиска позволяет вывести все ключи, находящиеся в дереве, в отсортированном порядке с помощью смешанного обхода (обхода in-order), излагаемого в п. 9.4.3.
Алгоритм поиска использует упорядоченность вершин дерева. Поиск выполняется следующим образом. Поиск начинается с корневой вершины, которая становится текущей. Затем аргумент поиска сравнивается с ключом текущей вершины. Если они равны, то поиск завершается результативно – текущая вершина является искомой вершиной. В противном случае, если аргумент поиска меньше ключа текущей вершины, то текущим становится левая дочерняя вершина. Если он больше, то текущей становится правая дочерняя вершина. Снова выполняется шаг сравнения. Со временем будет либо найден искомый элемент, либо встретится очередной указатель на дочерний элемент, который равен Nil, что свидетельствует об окончании поиска, который безуспешен.
Необходимо отметить одну особенность приведенного алгоритма в случае поиска по вторичному ключу. Если в дереве имеется несколько элементов с равными ключами, то не существует никаких гарантий, что будет найдена конкретная вершина с соответствующим ключом. Следовательно, дублирование ключей в дереве поиска не допускается. На практике различение ключей обеспечивается использованием, кроме главного ключа, дополнительного младшего ключа (или ключей). В результате определение дерева бинарного поиска будет формулироваться следующим образом: это дерево, в котором ключ левой дочерней вершины строго меньше ключа данной вершины, который, в свою очередь, строго меньше ключа правой дочерней вершины.
Алгоритм поиска в дереве бинарного поиска имитирует бинарный поиск в массиве. В каждой текущей вершине принимается решение об игнорировании вершин в одном из дочерних поддеревьев. Если дерево поиска сбалансировано (см. п. 9.4.2), алгоритм поиска является операцией типа О(log(N)), где N – число вершин в дереве.
Под сбалансированным деревом понимается дерево, в котором длина пути от корня до любого листа приблизительно одинакова, для разных листьев она может отличаться не более, чем на единицу. Сбалансированное дерево имеет минимальное количество уровней, необходимое для заданного количества вершин.
На рисунке 13.1 показаны два бинарных дерева поиска. Дерево на рисунке 13.1б менее эффективно для поиска, поскольку его высота равна 4, в отличие от дерева на рисунке 13.1а, высота которого равна 2.
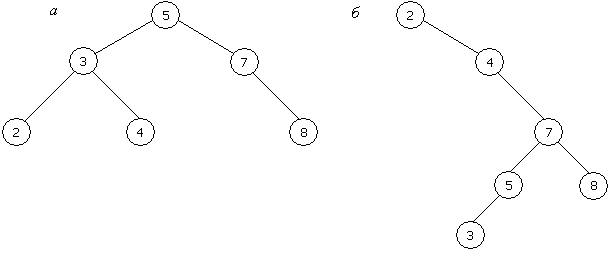
Рисунок 13.1 – Бинарные деревья поиска