Обход бинарного дерева
Методы обхода дерева любой степени, рассматриваемые в подразделе 10.3, переформулируем в отношении бинарных деревьев.
Нисходящий обход:
обработка корня,
нисходящий обход левого поддерева,
нисходящий обход правого поддерева.
Вершины дерева, изображенного на рисунке 9.8, поступали бы на обработку при обходе нисходящим методом в следующем порядке: a, b, d, h, i, e, c, f, g, j.
Смешанный обход:
смешанный обход левого поддерева,
обработка корня,
смешанный обход правого поддерева.
Например, при обходе дерева на рисунке 9.8 смешанным методом вершины обрабатываются в следующей последовательности: h, d, i, b, e, a, f, c, j, g.
Восходящий обход:
восходящий обход левого поддерева,
восходящий обход правого поддерева,
обработка корня.
Порядок обработки вершин того же дерева при восходящем обходе выглядит так: h, i, d, e, b, f, j, g, c, a.
Для методов обхода в применении к бинарным деревьям часто применяют специфичные названия: нисходящий обход называют обходом pre‑order, смешанный обход обходом in-order и восходящий обходом post‑order. Обход post‑order чаще всего применяется для уничтожения всех вершин в бинарном дереве, когда процесс уничтожения можно было бы описать следующим образом: «чтобы уничтожить все вершины бинарного дерева, необходимо уничтожить левое поддерево корня, затем правое поддерево, а затем и сам корень».
Все три метода легко представить рекурсивными процедурами. Прежде чем это сделать, необходимо определить процедуру, активируемую на этапе «обработка». Такая процедура должна выполнять некоторые действия над вершиной, к которой получен доступ на текущем шаге просмотра. А доступ к элементу связной структуры легче всего обеспечить через указатель, который назовем pNode. Текст такой процедуры может выглядеть, например, следующим образом:
Procedure ProcessingNode(pNode: Pvertex);
Var S: String;
Begin
S:= <преобразование информационных полей элемента рNode^ в строку>;
Form1.Memo1.Lines.Append(S);
End;
Теперь можно привести тексты трех подпрограмм обхода, которые реализуют приведенные выше рекурсивные алгоритмы:
Procedure PreOrder(pRoot: Pvertex);
Begin
If (aRoot <> Nil) Then Begin
ProcessingNode(pRoot);
PreOrder(pRoot^.Left);
PreOrder(pRoot^.Right);
End;
End;
Procedure InOrder(pRoot: Pvertex);
Begin
If (aRoot <> Nil) Then Begin
InOrder(pRoot^.Left);
ProcessingNode(pRoot);
InOrder(pRoot^.Right);
End;
End;
Procedure PostOrder(pRoot: Pvertex);
Begin
If (aRoot <> Nil) Then Begin
PostOrder(pRoot^.Left);
PostOrder(pRoot^.Right);
ProcessingNode(pRoot);
End;
End;
Для активации любой из этих трех процедур, следует воспользоваться вызовом в следующем виде:
<имя процедуры>(Root);
где Root указатель корня, например: PostOrder(Root).
Преобразование любого дерева к бинарному дереву
Любое m-арное дерево (т. е. дерево степени m) может быть преобразовано в эквивалентное ему бинарное дерево, которое проще исходного дерева с точки зрения представления в памяти и обработки. Графически такое преобразование сводится к следующим действиям:
сначала в каждом узле исходного дерева вычеркиваем все ветви, кроме самой левой ветви, которая соответствует ссылке на старшего сына;
в получившемся графе соединяем те узлы одного уровня, которые являются братьями в исходном дереве.
На рисунке 9.10 приведен пример такого преобразования, причем после него из некоторых элементов, исходят две ссылки: горизонтальная соединяет данный элемент с его младшим (в исходном дереве) братом, а вертикальная с его старшим сыном. Если на рисунке 9.10 повернуть все ссылки на 45° по часовой стрелке, то получим структуру, очень похожую на двоичное дерево. Однако считать ее таковым было бы ошибкой, поскольку функционально горизонтальные и вертикальные ссылки на рисунке 9.10 б имеют совершенно разный смысл. Правильнее было бы использовать следующую интерпретацию: после выполнения указанных преобразований из сыновей каждого родителя образуется линейный список, причем на старшего сына указывает ссылка от его родителя, а сам старший сын находится в голове списка своих братьев.
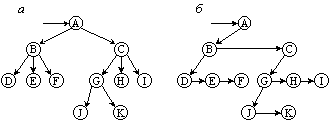
Рисунок 9.10 Преобразование 3-арного дерева к бинарному
Пользуясь аналогичным алгоритмом можно представить в виде двоичного дерева и лес. На рисунке 9.11 показаны этапы преобразования леса из двух деревьев в бинарное дерево.
Переход от m-арного дерева (или леса) к представлению в виде двоичного дерева при естественном связном хранении сокращает объем занимаемой памяти, поскольку каждый элемент m-арного дерева должен иметь m полей для логических указателей, тогда как элемент двоичного дерева имеет только два таких поля. С другой стороны, при таком преобразовании нужно помнить о функциональном назначении левой и правой ссылок и учитывать это при обработке дерева.
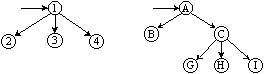
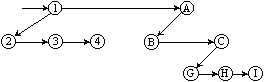
Рисунок 9.11 Преобразование леса к бинарному дереву