18 Розв’язок задачі теплопровідності в стержні має вид:

а) ;

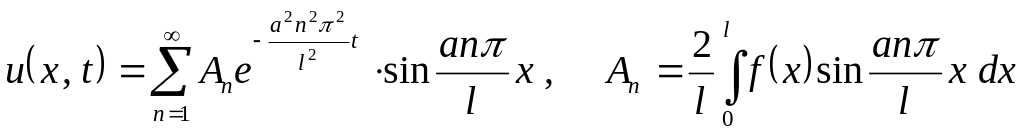б) ;

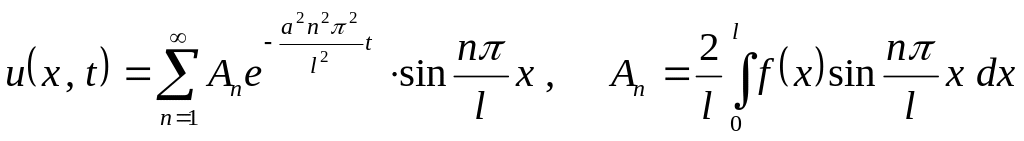в) ;

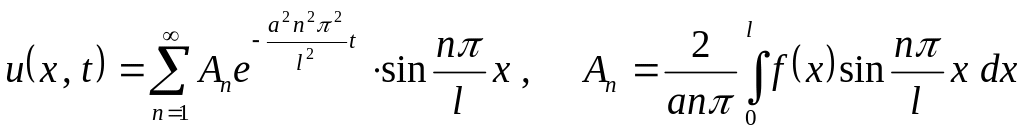г) ; д) інша відповідь.

Б .

Рівняння виду

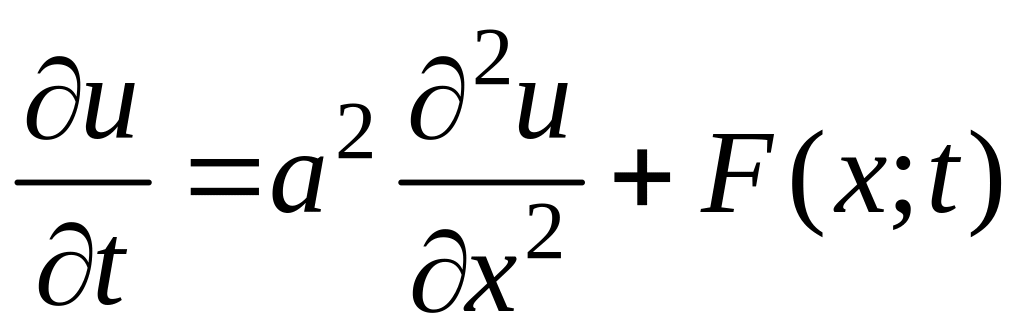
с крайовими умовами

і початковою умовою

описує закон розподілу температури в однорідному стрижні довжини l, на кінцях якого підтримується нульова температура. Функція F(x;t) характеризує існуючі усередині стрижня крапки (джерела) виділення або поглинання тепла. Якщо такі відсутні, F(x;t)=0 і рівняння називається однорідним.

19 Рівняння Лапласа в полярних координатах має вид:

а) ; б) ;

в) ; г) ; д) інша відповідь.

В .

Рівняння Лапласа - диференціальне рівняння в частинних похідних. У тривимірному просторі рівняння Лапласа записується так:

і є окремим випадком рівняння Гельмгольца.

У сферичних координатах рівняння має вигляд

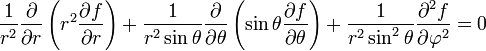
У полярних координатах r, φ рівняння має вигляд

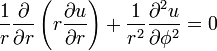
20 Розв’язок задачі Діріхле для круга має вид:

а) ;

б) ;

в) ;

г) ;

д) інша відповідь.

Б .

Нехай в площині 0ху є коло радіусом R з центром на початку координат і на його окружності задана деяка функція f(), де  - полярний кут. Потрібно знайти функцію u(r,), непреривну в колі, включаючи границю, задовільняючу всередині кола рівнянню Лапласа

.

і на колі що приймає задані значення .

.

Формула називається інтегралом Пуассона. Шляхом аналізу цієї формули доводиться, що якщо формула f() неперервна, то функція U(r,), визначена інтегралом задовільняє рівність (1) і при rR буде U(r,)f(), тобто U(r,) являє собою рішення поставленої задачі Діріхле для кола.

Рівtym c

1 Вказати тип рівняння .

а) еліптичний; б) гіперболічний; в) параболічний; г) сферичний; д) інша відповідь.

Б .

Запишемо таке рівняння щодо функції двох змінних у загальному виді:

.

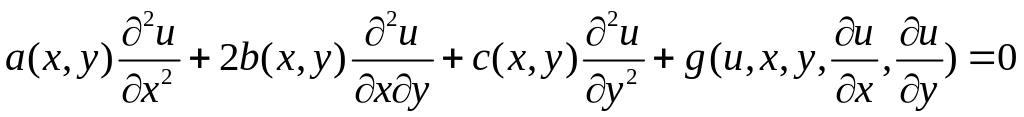Ці рівняння часто зустрічаються в математичних моделях фізичних процесів і теорія їхнього рішення найбільше добре розроблена.

Дискримінантом даного рівняння називається функція .

Говорять, що дане рівняння належить

• до еліптичного типу в області, де D<0

• до гіперболічного типу в області, де D>0

• до параболічного типу в області, де D=0.-

- гіперболічний тип

2 Вказати тип рівняння .

а) еліптичний; б) гіперболічний; в) параболічний; г) сферичний; д) інша відповідь.

А .

Запишемо таке рівняння щодо функції двох змінних у загальному виді:

.

Ці рівняння часто зустрічаються в математичних моделях фізичних процесів і теорія їхнього рішення найбільше добре розроблена.

Дискримінантом даного рівняння називається функція .

Говорять, що дане рівняння належить

• до еліптичного типу в області, де D<0

• до гіперболічного типу в області, де D>0

• до параболічного типу в області, де D=0.-

- еліптичний тип

3 Вказати тип рівняння .

а) еліптичний; б) гіперболічний; в) параболічний; г) сферичний; д) інша відповідь.

В .

Запишемо таке рівняння щодо функції двох змінних у загальному виді:

.

Ці рівняння часто зустрічаються в математичних моделях фізичних процесів і теорія їхнього рішення найбільше добре розроблена.

Дискримінантом даного рівняння називається функція .

Говорять, що дане рівняння належить

• до еліптичного типу в області, де D<0

• до гіперболічного типу в області, де D>0

• до параболічного типу в області, де D=0.-

- параболічний тип