Элементы логики предикатов.
Понятие предиката. Кванторы. Язык логики предикатов. Правильно построенные формулы. Тождественные преобразования формул. Правила вынесения кванторов и сколемизация. Понятие выводимости в логике предикатов. Правила логического вывода. Вывод на основе принципа резолюций.
Предикат – это …
а) функция одного либо нескольких аргументов с булевскими значениями истина и ложь.
б) отображение прямого произведения
заданных множеств во множество значений
истинности P:
{И,
Л}, где M1,
M2,.., Mn
– заданные множества; И, Л – символы
для обозначения соответственно истины
и лжи.
в) отображение суммы заданных множеств
во множество значений истинности P:
{И,
Л}, где M1,
M2,.., Mn
– заданные множества; И, Л – символы
для обозначения соответственно истины
и лжи.
г) отображение разности заданных множеств
во множество значений истинности P:
{И,
Л}, где M1,
M2,.., Mn
– заданные множества; И, Л – символы
для обозначения соответственно истины
и лжи.
д) функция одного либо нескольких аргументов, принимающая целочисленное значение.
Алфавит исчисления предикатов (первого порядка) содержит …
а) основные связки.
б) кванторы всеобщности.
в) дополнительные связки.
г) формулы.
д) предикаты.
Литеральной формулой (литералом) является …
а) х А(х)
б)
в) ¬А
г) х А(х)
д) А
НФБ-грамматика
<формула> ::= <атом> <формула> (<формула><формула>) <переменная><формула> <переменная><формула>
<атом> ::= <предикат>(<список термов>)
<список термов> ::= <терм><терм>,<список термов>
<терм> ::= <константа><переменная><функтор>(<список термов>)
определяет синтаксис …
а) формул исчисления высказываний.
б) формул исчисления предикатов.
в) формул чистого исчисления предикатов первого порядка.
г) формул чистого исчисления предикатов.
д) формул исчисления предикатов первого порядка.
Подформула А в формулах x A и x A называется …
а) областью действия квантора по х.
б) областью определения х.
в) областью значений х.
г) бескванторной формулой.
д) кванторной формулой.
Чистое исчисление предикатов не содержит …
а) предметных констант.
б) правил.
в) функторов.
г) предикатов.
д) собственных аксиом.
Прикладное исчисление предикатов – это …
а) исчисление предикатов, которое содержит предметные константы и/или функторы и/или предикаты и связывающие их собственные аксиомы
б) исчисление предикатов, которое не содержит предметных констант, функторов, предикатов и собственных аксиом
в) исчисление, в котором кванторы могут связывать не только предметные переменные, но и функторы, предикаты или иные множества объектов
г) исчисление предикатов, в котором кванторы могут связывать только предметные переменные, но не могут связывать функторы или предикаты
Исчисление предикатов первого порядка – это …
а) исчисление предикатов, которое содержит предметные константы и/или функторы и/или предикаты и связывающие их собственные аксиомы
б) исчисление предикатов, которое не содержит предметных констант, функторов, предикатов и собственных аксиом
в) исчисление, в котором кванторы могут связывать не только предметные переменные, но и функторы, предикаты или иные множества объектов
г) исчисление предикатов, в котором кванторы могут связывать только предметные переменные, но не могут связывать функторы или предикаты
Исчисление предикатов высшего порядка – это …
а) исчисление предикатов, которое содержит предметные константы и/или функторы и/или предикаты и связывающие их собственные аксиомы
б) исчисление предикатов, которое не содержит предметных констант, функторов, предикатов и собственных аксиом
в) исчисление, в котором кванторы могут связывать не только предметные переменные, но и функторы, предикаты или иные множества объектов
г) исчисление предикатов, в котором кванторы могут связывать только предметные переменные, но не могут связывать функторы или предикаты
Первая теорема Геделя о неполноте:
а) Во всякой достаточно богатой теории 1-ого порядка существует такая истинная формула F, что ни F, ни F не являются выводимыми в этой теории.
б) Во всякой достаточно богатой теории 3-ого порядка существует такая истинная формула F, что ни F, ни F не являются выводимыми в этой теории.
в) Ни в одной достаточно богатой теории 1-ого порядка не существует такая истинная формула F, что ни F, ни F не являются выводимыми в этой теории.
Вторая теорема Геделя о неполноте:
а) Во всякой достаточно богатой теории первого порядка формула F, утверждающая непротиворечивость этой теории, не является выводимой в ней
б) Во всякой достаточно богатой теории второго порядка формула F, утверждающая непротиворечивость этой теории, не является выводимой в ней
в) Во всякой достаточно богатой теории первого порядка формула F, утверждающая противоречивость этой теории, является выводимой в ней
Резолютивный вывод Ф из множества дизъюнктов S …
а) есть такая конечная последовательность Ф1,…, Фk дизъюнктов, что Фk=Ф и каждый дизъюнкт Фi или принадлежит S, или является резольвентой дизъюнктов, предшествующих Фi.
б) есть такая бесконечная последовательность Ф1,…, Фk (К(1, +∞)), дизъюнктов, что Фk=Ф и каждый дизъюнкт Фi или принадлежит S, или является резольвентой дизъюнктов, предшествующих Фi.
в) есть такая конечная последовательность Ф1,…, Фk конъюнктов, что Фk=Ф и каждый конъюнкт Фi или принадлежит S, или является резольвентой конъюнктов, предшествующих Фi.
Универсальным замыканием формулы Ф (x1,…, xn) называется …
а) предложение
x1…
xn
Ф (x1,…,
xn).
б) предложение x1…xn Ф (x1,…, xn).
в) предложение x1…xn Ф (x1,…, xn).
г) предложение x1…xn Ф (x1,…, xn).
д) предложение x1…xn Ф (x1,…, xn).
Теорема о полноте метода резолюций:
а) Если S - множество дизъюнктов, то множество универсальных замыканий формул из S невыполнимо тогда и только тогда, когда существует резолютивный вывод 0 из S.
б) Если S - множество конъюнктов, то множество универсальных замыканий формул из S невыполнимо тогда и только тогда, когда существует резолютивный вывод 0 из S.
в) Если S - множество дизъюнктов, то множество универсальных замыканий формул из S выполнимо тогда и только тогда, когда существует резолютивный вывод 0 из S.
г) Если S - множество конъюнктов, то множество универсальных замыканий формул из S выполнимо тогда и только тогда, когда не существует резолютивный вывод 0 из S.
Методом резолюций в исчислении предикатов называется правило вывода:
а)
,
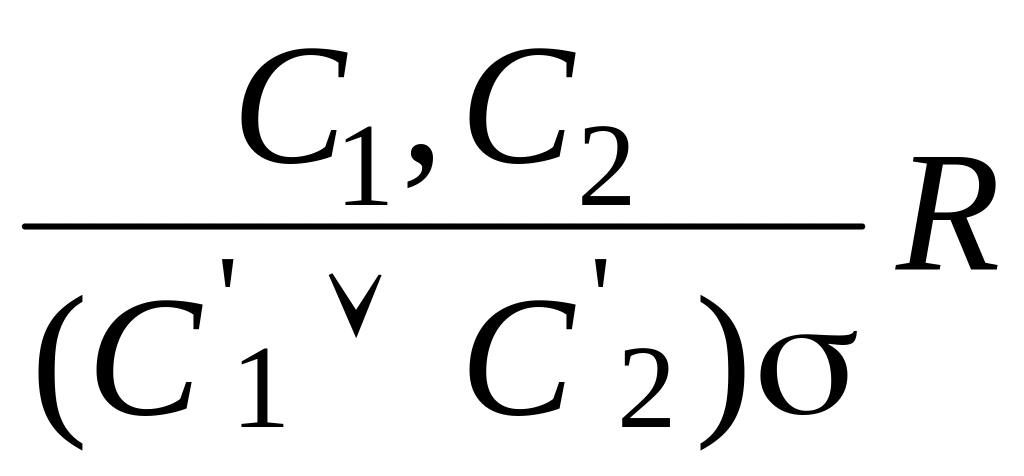если в предложениях C1
и C2
унифицируемые
литералы P1
и P2,
т. е. C1=P1VC`1
и C2=P2VC`2.
б)
,
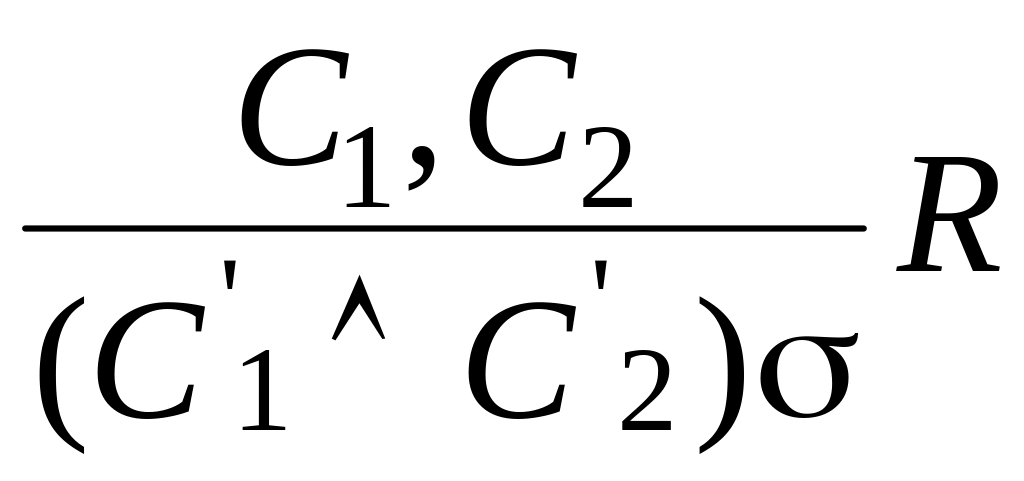если в предложениях C1
и C2
унифицируемые
литералы P1
и P2,
т. е. C1=P1VC`1
и C2=P2VC`2.
в)
,
если в предложениях C1
и C2
унифицируемые
литералы P1
и P2,
т. е. C1=P1VC`1
и C2=P2VC`2.
г)
,
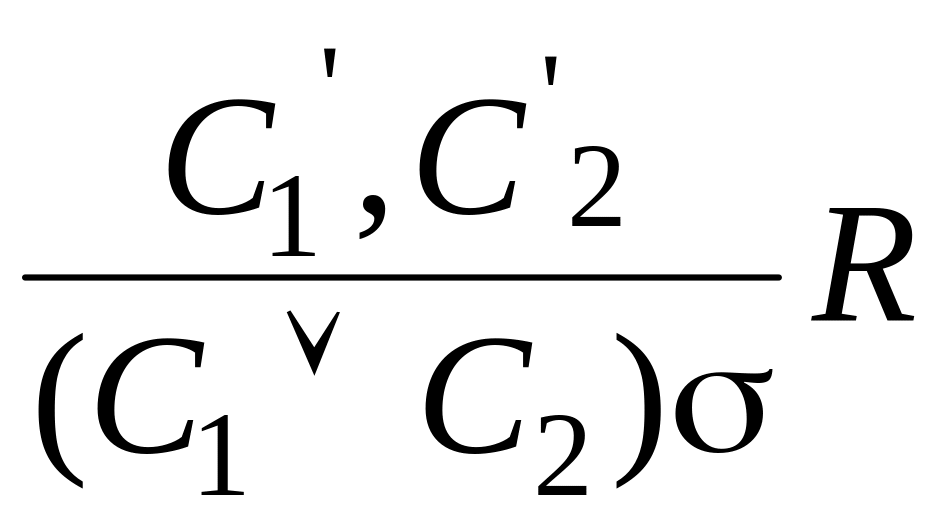если в предложениях C1
и C2
унифицируемые
литералы P1
и P2,
т. е. C1=P1VC`1
и C2=P2VC`2.
К основным положениям метода резолюций относятся:
а) Модель исследуемого “мира” представляется множеством аксиом, которые преобразуются в множество дизъюнктов S.
б) Доказательство противоречивости сводится к доказательству того, что из данного множества дизъюнктов может быть выведен пустой дизъюнкт.
в) Для уменьшения числа резольвент (и следовательно, для повышения эффективности вывода) очень существенна стратегия вывода.
г) Если множество дизъюнктов S противоречиво, то пустой дизъюнкт будет найден за конечное число шагов. При непротиворечивости множества дизъюнктов S процесс установления факта непротиворечивости может быть бесконечным.
д) В техническом аспекте метод резолюций состоит из унификаций и получения множества резольвент до тех пор, пока не будет получена пустая резольвента.
е) Для доказательства справедливости теорем в данном “мире” необходимо взять её отрицание и, преобразовав в форму дизъюнкнта, добавить к множеству S. Если теорема верна, то новое множество дизъюнктов должно быть противоречиво.
Какие из следующих предложений являются предикатами?
а) x делится на 3 (x N).
б) y = x2; x R.
в) x2 + y2 = 0; x, y R.
г) x2+ x + 1; x R.
д) Для всякого x R найдется y R такой, что x = y + 1.
Пусть М – множество точек, прямых и плоскостей 3-мерного евклидова пространства со следующими предикатами: Т(х) = И х – точка; Пр(х) = И х – прямая; Пл(х) = И х – плоскость; Л(х, у) = И х лежит на у. Записью формулы «через каждые две точки можно провести прямую» является …
а) x y (T(x) & T(y) z (П(z) & Л(x, z) & Л(y, z))).
б) x y (T(x) & T(y) z (П(z) & Л(x, z) & Л(y, z))).
в) x y (T(x) & T(y) & z (П(z) & Л(x, z) & Л(y, z))).
г) x y (T(x) & T(y) z (П(z) & Л(x, y))).
д) x y (T(x) & T(y) & z (П(z) & Л(x, z) & Л(y, z))).
Пусть М – множество точек, прямых и плоскостей 3-мерного евклидова пространства со следующими предикатами: Т(х) = И х – точка; Пр(х) = И х – прямая; Пл(х) = И х – плоскость; Л(х, у) = И х лежит на у. Записью формулы «через каждые три точки, не лежащие на одной прямой можно провести единственную плоскость» является …
а) x y z (T(x) & T(y) & T(z) & ( ( s (Пр(s) & Л(x, s) & Л(y, s) & Л(z, s))))) p (Пл(p) & Л(x, p) & Л(y, p) & Л(z, p)).
б) x y z (T(x) & T(y) & T(z) & ( ( s (Пр(s) & Л(x, s) & Л(y, s) & Л(z, s))))) p (Пл(p) & Л(x, p) & Л(y, p) & Л(z, p) & u (u≠p & Л(x, u) & Л(y, u) & Л(z, u))).
в) x y z (T(x) & T(y) & T(z) & ( ( s (Пр(s) & Л(x, s) & Л(y, s) & Л(z, s))))) p (Пл(p) & Л(x, p) & Л(y, p) & Л(z, p)).
г) x y z (T(x) & T(y) & T(z) & ( ( s (Пр(s) & Л(x, s) & Л(y, s) & Л(z, s))))) p (Пл(p) & Л(x, p) & Л(y, p) & Л(z, p)).
д) x y z s (T(x) & T(y) & T(z) & Пр(s) & Л(x, s) & Л(y, s) & Л(z, s)) p (Пл(p) & Л(x, p) & Л(y, p) & Л(z, p)).
Какие из формул являются невыполнимыми?
а) x P(x).
б) x P(x).
в) x y (Q(x,x) & Q(x,y)).
г) x y (P(x) & P(y)).
д) xy (Q(x,y) z R(x, y, z)).
е) P(x) y P(y).
Какие из формул являются тождественной истинными?
а) (x P(x) x P(x)).
б) (x P(x) x P(x)).
в) xy Q(x,y) yx Q(x,y).
г) xy Q(x,y) yx Q(x,y).
Какие последовательности являются выводами в исчислении предикатов?
а) (xyA(x,y))yA(y,y)
б) x P(x)P(y); x P(x) y P(y)
в) A(x) x A(x);
(A(x) x A(x)) (x A(x) (A(x) x A(x)));
x A(x) (A(x) x A(x))