
- •3. Случайные векторы
- •3.1. Понятие случайного вектора. Ряд распределения двумерного дискретного случайного вектора
- •3.2. Функция и плотность распределения случайного вектора
- •3.3. Зависимость и независимость св
- •3.4. Условные законы распределения св
- •3.5. Корреляционный момент и коэффициент корреляции двух св
- •3.6. Многомерное нормальное распределение
- •4. Функции случайных величин
- •4.1. Математическое ожидание и дисперсия функции случайных величин
- •4.2. Плотность вероятности монотонной функции непрерывной св. Плотность вероятности линейной функции нормально распределённой св
- •4.3. Распределения “хи-квадрат”, Стьюдента и Фишера
- •4.4. Основные свойства математического ожидания
- •4.5. Основные свойства дисперсии и коэффициента корреляции
- •5. Предельные теоремы
- •5.1. Закон больших чисел
- •5.2. Центральная предельная теорема
- •6. Случайные процессы
- •6.1. Понятие случайного процесса. Функции и плотности распределения случайного процесса
- •6.2. Математическое ожидание, дисперсия и автокорреляционная функция случайного процесса. Понятие стационарного случайного процесса
- •6.3. Дискретная цепь Маркова: основные понятия и свойства
4. Функции случайных величин
4.1. Математическое ожидание и дисперсия функции случайных величин
Пусть имеется СВ Х с заданным законом
распределения. Другая СВ Y связана
с СВ Х зависимостью
![]() ,
где
,
где
![]() – заданная функция. Последнее означает,
что если СВ Х принимает некоторое
значение х, то СВ Y принимает
значение
,
т.е. значение СВ Y однозначно
определяется значением СВ Х. Требуется
найти математическое ожидание и дисперсию
СВ Y.
– заданная функция. Последнее означает,
что если СВ Х принимает некоторое
значение х, то СВ Y принимает
значение
,
т.е. значение СВ Y однозначно
определяется значением СВ Х. Требуется
найти математическое ожидание и дисперсию
СВ Y.
Пусть Х – дискретная СВ с возможными
значениями
![]() и их вероятностями
и их вероятностями
![]() .
Поскольку
.
Поскольку
![]() ,
,
![]() ,
то Y – дискретная СВ с возможными
значениями
,
то Y – дискретная СВ с возможными
значениями
![]() ,
вероятности которых равны
,
а если какое-нибудь значение повторяется,
то его вероятность равна сумме
соответствующих вероятностей. Из формул
для математического ожидания и дисперсии
дискретной СВ получим
,
вероятности которых равны
,
а если какое-нибудь значение повторяется,
то его вероятность равна сумме
соответствующих вероятностей. Из формул
для математического ожидания и дисперсии
дискретной СВ получим
![]() ,
,
![]() .
.
Отметим, что значения
![]() в общем случае не упорядочены по
возрастанию, а некоторые из них могут
совпадать. Однако от перестановки и
объединения слагаемых под знаком суммы
значения
в общем случае не упорядочены по
возрастанию, а некоторые из них могут
совпадать. Однако от перестановки и
объединения слагаемых под знаком суммы
значения
![]() и
и
![]() ,
очевидно, не изменяются.
,
очевидно, не изменяются.
Если Х – непрерывная СВ с плотностью
вероятности
![]() ,
то заменяя суммирование интегрированием,
а вероятности – элементами вероятности,
можно получить формулы
,
то заменяя суммирование интегрированием,
а вероятности – элементами вероятности,
можно получить формулы
![]() ,
,
![]() .
.
Замечание. Из всех приведённых формул видно, что для вычисления математического ожидания и дисперсии СВ Y не нужно находить её закон распределения, а достаточно знать только закон распределения СВ Х.
Аналогичные формулы существуют для
математического ожидания и дисперсии
функции двух СВ. Пусть СВ Z связана
с СВ Х и Y зависимостью
![]() ,
где
,
где
![]() – заданная функция. Тогда если Х и
Y – дискретные СВ с возможными
значениями
– заданная функция. Тогда если Х и
Y – дискретные СВ с возможными
значениями
![]() и
и
![]() и известны вероятности
и известны вероятности
![]() ,
,
![]() ,
,
то
,
,
то
![]() ,
,
![]() .
.
Если Х и Y – непрерывные СВ и
известна плотность
![]() ,
то
,
то
![]() ,
,![]() .
.
Приведённые формулы имеют естественное обобщение на случай функции произвольного числа СВ.
4.2. Плотность вероятности монотонной функции непрерывной св. Плотность вероятности линейной функции нормально распределённой св
Теорема. Пусть Х – непрерывная
СВ с плотностью вероятности
,
а
![]() – дифференцируемая и строго монотонная
на R функция. Тогда
плотность вероятности
– дифференцируемая и строго монотонная
на R функция. Тогда
плотность вероятности
![]() СВ
определяется равенством
СВ
определяется равенством
![]() .
.
Доказательство. Пусть
![]() дифференцируема и строго возрастает,
тогда обратная функция
дифференцируема и строго возрастает,
тогда обратная функция
![]() тоже дифференцируема и строго возрастает,
а значит, при любом
тоже дифференцируема и строго возрастает,
а значит, при любом
![]() событие
равносильно событию
событие
равносильно событию
![]() .
Следовательно, для функции распределения
.
Следовательно, для функции распределения
![]() СВ Y имеем
СВ Y имеем
![]() ,
,
где
![]() – функция распределения СВ Х.
Дифференцируя полученное равенство по
у, получим
– функция распределения СВ Х.
Дифференцируя полученное равенство по
у, получим
![]() .
Если
строго убывает, то
тоже строго убывает и при любом
событие
равносильно событию
.
Если
строго убывает, то
тоже строго убывает и при любом
событие
равносильно событию
![]() ,
т.е.
,
т.е.
![]()
![]() ,
,
откуда
![]() .
Поскольку
.
Поскольку
![]() неотрицательна, а производная возрастающей
(убывающей) функции положительна
(отрицательна), то в обоих случаях
.
неотрицательна, а производная возрастающей
(убывающей) функции положительна
(отрицательна), то в обоих случаях
.
Пусть, далее,
![]() и
и
![]() ,
,
![]() ,
т.е. Y – линейная функция нормально
распределённой СВ. Используя утверждение
приведённой теоремы, найдём плотность
вероятности СВ Y. Имеем
,
т.е. Y – линейная функция нормально
распределённой СВ. Используя утверждение
приведённой теоремы, найдём плотность
вероятности СВ Y. Имеем
![]() ,
,
![]() ,
,
![]() .
.
Поскольку
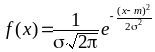 ,
то
,
то
 .
.
Отсюда видно, что закон распределения
линейной функции
,
нормально распределённого аргумента
Х также является нормальным, причём
![]() ,
,
![]() .
.
