
- •Рекомендуемая литература
- •Теория вероятностей
- •1. Случайные события
- •1.1. Событие и эксперимент. Соотношения между событиями. Пространство элементарных событий
- •1.2. Частота события. Статистическое определение вероятности
- •1.3. Классическое определение вероятности
- •1.4. Геометрическое определение вероятности
- •1.5. Аксиомы теории вероятностей. Основные следствия из аксиом
- •1.6. Условная вероятность. Независимость событий. Теорема умножения вероятностей
- •1.7. Теорема сложения вероятностей
- •1.8. Формула полной вероятности. Формула Байеса
- •1.9. Вычисление вероятностей событий с помощью биномиальной и полиномиальной формул
- •2. Случайные величины
- •2.1. Понятие случайной величины и её закона распределения. Дискретные и непрерывные величины
- •2.2. Ряд и многоугольник распределения дискретной св
- •2.3. Функция распределения св и её свойства
- •2.4. Плотность распределения непрерывной св и её свойства
- •2.5. Математическое ожидание, мода и квантили св
- •2.6. Моменты, дисперсия и среднее квадратическое отклонение св
- •2.7. Биномиальное распределение
- •2.8. Распределение Пуассона
- •2.9. Геометрическое распределение
- •2.10. Равномерное распределение
- •2.11. Показательное распределение
- •2.12. Одномерное нормальное распределение
2.2. Ряд и многоугольник распределения дискретной св
Пусть Х – дискретная СВ, имеющая
конечное множество возможных значений
![]() ,
расположенных в порядке возрастания,
и
,
расположенных в порядке возрастания,
и
![]() ,
.
Тогда простейшей формой закона
распределения СВ Х является следующая
таблица, называемая рядом распределения:
,
.
Тогда простейшей формой закона
распределения СВ Х является следующая
таблица, называемая рядом распределения:
-
Х
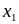
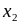
. . .
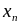
Р
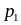
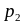
. . .

События
![]() ,
являются попарно несовместными и
образуют полную группу, поэтому
,
являются попарно несовместными и
образуют полную группу, поэтому
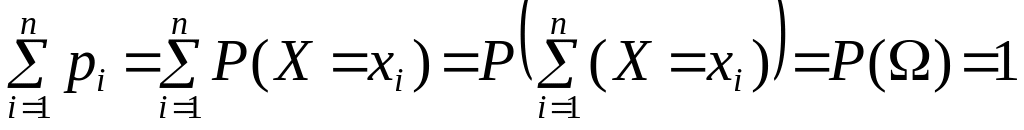 .
.
Для наглядности ряд распределения можно
представить графически: на координатной
плоскости изображаются точки
![]() ,
,
которые последовательно соединяются
отрезками прямых. Полученная ломаная
называется многоугольником распределения.
,
,
которые последовательно соединяются
отрезками прямых. Полученная ломаная
называется многоугольником распределения.
Если дискретная СВ имеет счётное
множество возможных значений
![]() ,
расположенных в порядке возрастания,
то её закон распределения может быть
задан формулой вида
,
расположенных в порядке возрастания,
то её закон распределения может быть
задан формулой вида
![]() ,
,
![]() ,
где р – некоторая функция натурального
аргумента и выполняется условие
,
где р – некоторая функция натурального
аргумента и выполняется условие
![]() .
Указанная формула также называется
рядом распределения.
.
Указанная формула также называется
рядом распределения.
2.3. Функция распределения св и её свойства
Функцией распределения СВ Х называется
такая функция
![]() ,
которая при каждом значении числового
аргумента х равна вероятности того,
что СВ Х принимает значение, меньшее
х, т.е.
,
которая при каждом значении числового
аргумента х равна вероятности того,
что СВ Х принимает значение, меньшее
х, т.е.
![]() .
Из определения СВ следует, что
.
Из определения СВ следует, что
![]() определена при любом значении х.
Функция распределения является одной
из форм закона распределения как
дискретной, так и непрерывной СВ.
определена при любом значении х.
Функция распределения является одной
из форм закона распределения как
дискретной, так и непрерывной СВ.
Рассмотрим основные свойства .
10.
![]() .
.
Доказательство следует из определения
как вероятности:
![]() .
.
20.
– неубывающая функция аргумента х,
т.е. если
,
то
![]() .
.
Доказательство. Пусть
.
Событие
![]() есть сумма несовместных событий
и
есть сумма несовместных событий
и
![]() ,
поэтому из аксиомы сложения имеем
,
поэтому из аксиомы сложения имеем
![]() или
или
![]() ,
откуда
,
откуда
![]() ,
т.е.
.
,
т.е.
.
30.
![]() .
.
Доказательство следует из полученного выше равенства
![]() .
.
40.
![]() ,
,
![]() .
.
Доказательство. Рассмотрим значение
СВ Х как положение случайной точки
на числовой оси. Тогда функция
при каждом значении х равна вероятности
того, что случайная точка окажется левее
точки х. При неограниченном перемещении
точки х влево (вправо) попадание
случайной точки левее х в пределе
становится невозможным (достоверным)
событием, поэтому
![]() ,
,
![]() .
.
50. Функция распределения дискретной СВ постоянна на любом интервале, не содержащем возможных значений этой СВ, и имеет скачок в каждой точке, совпадающей с возможным значением, при этом величина скачка равна вероятности появления соответствующего значения.
60. Функция распределения непрерывной СВ непрерывна на всей числовой оси. Функция распределения произвольной СВ при любом значении аргумента х непрерывна слева.
2.4. Плотность распределения непрерывной св и её свойства
Пусть Х – непрерывная СВ, а
– её функция распределения. Плотностью
распределения (или плотностью вероятности)
СВ Х называется функция
![]() ,
равная производной от функции распределения
этой СВ, т.е.
,
равная производной от функции распределения
этой СВ, т.е.
![]() .
Если при некотором значении аргумента
недифференцируема, то
в этой точке не определена.
.
Если при некотором значении аргумента
недифференцируема, то
в этой точке не определена.
Разность
![]() равна вероятности попадания СВ на
участок
равна вероятности попадания СВ на
участок
![]() ,
поэтому отношение
,
поэтому отношение
![]() есть средняя вероятность, приходящаяся
на единицу длины этого участка. Это
означает, что
характеризует “плотность вероятности”,
с которой распределены возможные
значения СВ. Если
дифференцируема в точке х, то при
малом
есть средняя вероятность, приходящаяся
на единицу длины этого участка. Это
означает, что
характеризует “плотность вероятности”,
с которой распределены возможные
значения СВ. Если
дифференцируема в точке х, то при
малом
![]() имеет место
имеет место
![]() ,
,
где величина
![]() называется элементом вероятности.
называется элементом вероятности.
Рассмотрим основные свойства плотности распределения.
10.
![]() .
.
Доказательство следует из равенства
![]() и неубывания
.
и неубывания
.
20.
![]() .
.
Доказательство.
![]() .
.
30.
![]() .
.
Доказательство.
![]() .
.
40.
![]() .
.
Доказательство.
![]() .
.
Замечание. Для непрерывной СВ Х
при любых
имеет место
![]() ,
поэтому
,
поэтому
![]() .
.
Функция распределения непрерывной СВ называется также её интегральным законом, а плотность вероятности – дифференциальным законом распределения. График плотности называется кривой распределения.
