
- •Введение
- •1. Ретроспективный анализ развития научно-технического направления «надежность технических систем»
- •2. Некоторые характеристики случайных величин, событий, процессов в оценках надежности технических систем
- •2.1. Основные понятия, непосредственный подсчет вероятностей.
- •2.2. Теоремы сложения и умножения вероятностей.
- •2.3. Формула полной вероятности
- •2.4. Повторение опытов.
- •3. Основные понятия и количественные характеристики надежности технических систем
- •3.1. Предмет надежности.
- •3.2. Причины недостаточной надежности технических систем.
- •3.3. Цена надежности.
- •3.4. Основные понятия теории надежности.
- •3.5. Основные количественные характеристики надежности и связь между ними.
- •3.6. Характеристики технических систем, используемые в теории надежности.
- •4. Надежность элементов технических систем.
- •4.1. Основные виды отказов элементов технических систем.
- •4.2. Кривая распределения отказов элементов.
- •4.3. Особенности распределения отказов элементов по вине производства.
- •4.4. Законы распределения внезапных отказов элементов.
- •4.5. Законы распределения постепенных отказов (отказов по старению).
- •4.6. Дифференциальный закон распределения времени исправной работы элемента с учетом отказов по вине производства, внезапных отказов и отказов по причине старения.
- •4.7. Расчетно-графическая работа № 1.
- •5. Методы оценки надежности нерезервированных невосстанавливаемых систем.
- •5.1. Сложные технические системы и определение их надежности.
- •5.2. Оценка надежности последовательных систем без накопления нарушений при наличии только внезапных отказов элементов.
- •5.3. Оценка надежности последовательных сложных систем без накопления нарушений с учетом старения (износа) элементов.
- •5.4. Расчетно-графическая работа № 2.
- •6. Определение надежности технических систем при постоянно включенном резерве («горячее» резервирование).
- •6.1. Количественные показатели надежности резервированной системы с постоянно включенным резервом.
- •6.2. Расчетно-графическая работа № 3.
- •7. Нагрузочное резервирование.
- •7.1. Теоретические предпосылки решения задачи расчета надежности технической системы, резервированной по принципу «теплого» резерва.
- •7.2. Расчетно-графическая работа № 4.
- •8. Вероятность безотказной работы технической системы при резервировании замещением («холодное» резервирование)
- •8.1. Расчетные соотношения для случая резервирования при идеальных переключающих устройствах (коммутаторах)
- •8.2. Влияние переключающих устройств (коммутаторов) на качество резервирования замещением (на качество «холодного» резервирования).
- •8.3. Расчетно-графическая работа № 5
- •9. Логико-вероятностные методы исследования надежности технических систем
- •9.1. Некоторые сведения из основ алгебры логики.
- •9.2. Основные логические операции.
- •9.3. Значимость элемента в системе.
- •10. Надежность технических систем с восстановлением
- •10.1. Оценка надежности технических систем при мгновенном восстановлении устройств
- •10.2. Надежность системы с задержанным восстановлением
- •10.3. Определение надежности сложной восстанавливаемой системы
- •10.4. Практические аспекты исследования надежности восстанавливаемых технических систем
- •10.4.1. Показатели надежности восстанавливаемых нерезервированных систем
- •10.4.2. Показатели надежности резервированных восстанавливаемых систем
- •10.4.3. Вероятность безотказной работы резервированных восстанавливаемых систем
- •Заключение
4.5. Законы распределения постепенных отказов (отказов по старению).
Постепенные отказы могут иметь различные законы распределения. Причиной постепенных отказов являются необратимые физико-химические процессы, протекающие в структуре элементов технически систем и приводящие к изменению их входных параметров или характеристик.
Поскольку изменение параметра во времени может носить случайный характер, то кривую изменения конкретного параметра данного элемента следует считать реализацией случайной функции X(t).
Случайной функцией X(t) называется функция, значение которой при каждом данном значении аргумента t является случайной величиной.
Характер распределения времени исправной работы элемента по старению (износу) зависит от начального распределения свойств элемента по параметру X в точке t=0 и вида случайного процесса изменения данного свойства.
Таким образом, в простейшей постановке задача определения закона распределения времени исправной работы элемента технической системы по старению сводится к задаче нахождения искомого закона по известным законам распределения параметра в одном или нескольких сечениях tj случайной функции X(t).
4.6. Дифференциальный закон распределения времени исправной работы элемента с учетом отказов по вине производства, внезапных отказов и отказов по причине старения.
Сделаем следующие допущения.
Распределение времени отказов по вине производства распределено по закону Вейбулла с параметрами:
= 0, b 1, c 0.5, t[0, t1].
где t1 –– окончание этапа приработки технической системы.
Распределение времени возникновения неисправностей в результате аварий и поломок (внезапные отказы) подчинено экспоненциальному закону с параметром для t[t1, t2],
где t2 –– начало этапа старения элементов системы.
Распределение времени отказов при учете только аварий по причине старения (износа) подчинено нормальному закону с параметрами T0 и 0.
События, заключающиеся в выходе из стоя элементов по причине производства, внезапных отказов и по причине старения, совместны и независимы.
Принятые допущения не вносят существенных ошибок в определение показателей надежности технических систем по следующим причинам:
внезапные отказы редки, а их интенсивность во времени постоянна;
число факторов, влияющих на выход элементов из строя по причине старения велико и все причины практически равнозначны, что позволяет сделать вывод о том, что плотность распределения времени исправной работы элемента по старению подчинена закону, близкому к нормальному;
совместность выхода из строя элементов по производственным дефектам, старению и по причине внезапной аварии не вызывает сомнений, но случаи выхода элементов из строя по трем причинам чрезвычайно редки, поэтому условием совместности иногда допустимо пренебречь.
Таким образом, любой элемент можно представить в виде системы, состоящей из трех условных элементов, соединенных в смысле надежности последовательно.
Будем полагать, что отказы одного условного элемента происходят только в результате производственных недоработок, второго –– по причине аварий или поломок, а третьего–– только в результате износа или старения.
Плотность распределения времени исправной работы первого элемента:
![]() (4.22)
для второго
элемента:
(4.22)
для второго
элемента:
![]() (4.23)
для третьего
элемента:
(4.23)
для третьего
элемента:
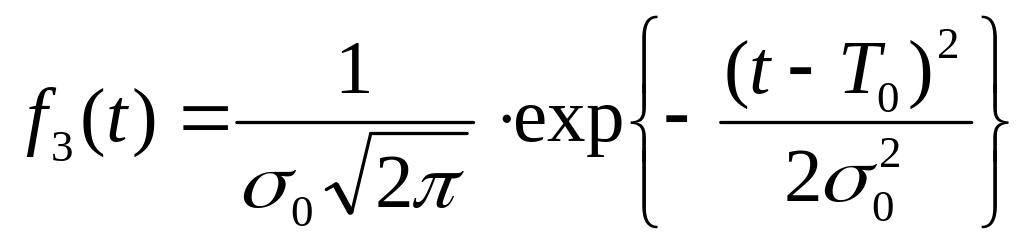 (4.24)
Надежность
этих условных элементов определяется
соответственно:
(4.24)
Надежность
этих условных элементов определяется
соответственно:
![]() (4.25)
(4.25)
![]() (4.26)
(4.26)
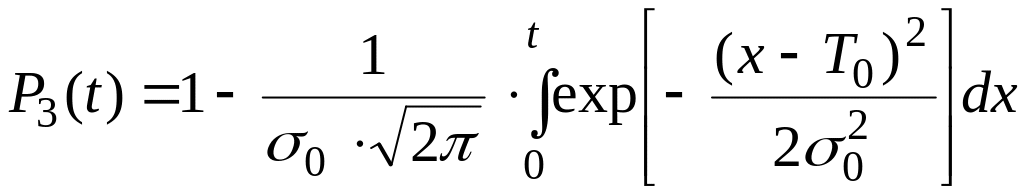 (4.27)
(4.27)
Система, состоящая из трех последовательно соединенных условных элементов, будет исправной только тогда, когда все три элемента будут исправны.
В этом случае формула для определения вероятности исправной работы элемента (состоящего из трех условных элементов) будет иметь вид:
![]() (4.28)
Плотность
распределения времени исправной работы
определится через вероятность
соотношением:
(4.28)
Плотность
распределения времени исправной работы
определится через вероятность
соотношением:
![]() (4.29)
тогда,
учитывая:
(4.29)
тогда,
учитывая:
![]()
![]() (4.30)
получим:
(4.30)
получим:
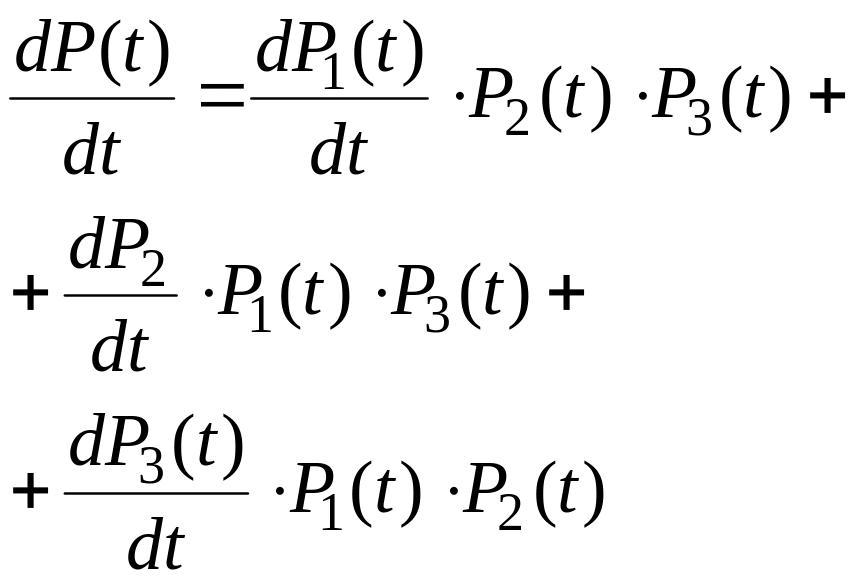 (4.31)
(4.31)
