5.4. Расчетно-графическая работа № 2.
Исследование надежности нерезервированной технической системы в период нормальной эксплуатации (без учета старения элементов).
Основными показателями надежности нерезервированных невосстанавливаемых систем являются:
Pc(t) –– вероятность безотказной работы системы в течение времени t;
TС –– среднее время безотказной работы системы.
При постоянных значениях (неизменяемых во времени) интенсивностей отказов элементов, имеем:
,
где С –– интенсивность отказов системы
Исходные данные для выполнения лабораторной работы:
число элементов системы n=10; время Т непрерывной работы системы; интенсивности i отказов каждого элемента.
Время непрерывной работы системы дано для определения вероятности безотказной работы системы в течение этого времени.
Требуется:
определить интенсивность отказов системы; определить ожидаемое время безотказной работы системы; построить функцию изменения вероятности безотказной работы системы; вычислить вероятность нахождения системы в рабочем состоянии в течение времени ее непрерывной работы; определить верхнюю и нижнюю границы вероятности безотказной работы системы в течение времени ее непрерывной работы.
Значения интенсивностей отказов элементов i10-5 1/час и времени непрерывной работы (час) для выполнения расчетной работы № 2.
Таблица 1
В
Эл-т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
i=1 |
2.4 |
0.3 |
5.5 |
0.4 |
3.5 |
0.7 |
0.7 |
3.1 |
4.4 |
1.0 |
4.3 |
0.5 |
7.1 |
1.8 |
i=2 |
1.7 |
0.7 |
4.8 |
0.5 |
4.8 |
0.5 |
0.4 |
2.0 |
2.0 |
1.4 |
4.2 |
0.1 |
7.2 |
1.4 |
i=3 |
3.3 |
1.1 |
3.9 |
0.9 |
8.7 |
0.4 |
9.3 |
1.5 |
2.4 |
1.2 |
3.6 |
0.4 |
7.0 |
1.9 |
i=4 |
0.8 |
0.2 |
2.7 |
0.5 |
5.5 |
1.9 |
4.2 |
2.2 |
2.6 |
1.6 |
2.8 |
6.6 |
6.5 |
1.2 |
i=5 |
0.3 |
0.8 |
8.1 |
0.3 |
4.9 |
1.7 |
5.3 |
0.3 |
2.5 |
1.8 |
9.1 |
3.1 |
3.3 |
1.1 |
i=6 |
1.4 |
0.4 |
0.5 |
0.2 |
6.6 |
0.7 |
1.1 |
0.4 |
2.1 |
1.9 |
1.0 |
0.2 |
4.3 |
0.3 |
i=7 |
2.6 |
1.5 |
0.3 |
0.7 |
6.9 |
6.1 |
1.5 |
2.6 |
2.0 |
1.4 |
0.2 |
0.1 |
0.1 |
0.2 |
i=8 |
5.1 |
1.2 |
4.6 |
0.4 |
4.2 |
1.2 |
3.2 |
1.1 |
2.3 |
1.2 |
0.1 |
0.7 |
0.2 |
4.0 |
i=9 |
2.9 |
2.0 |
5.3 |
1.3 |
8.7 |
0.1 |
2.7 |
1.7 |
0.1 |
1.1 |
0.3 |
4.5 |
3.3 |
1.1 |
i=10 |
1.3 |
0.9 |
3.3 |
1.0 |
9.1 |
0.3 |
2.2 |
1.0 |
0.1 |
1.9 |
2.2 |
4.3 |
2.8 |
0.5 |
Т1000 |
2.9 |
1.2 |
2.3 |
2.5 |
2.1 |
2.2 |
1.7 |
2.0 |
1.8 |
2.1 |
1.9 |
2.7 |
1.7 |
1.4 |
ар-нтПродолжение таблицы 1.
В ар-нт
Эл-т |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
i=1 |
1.4 |
0.5 |
5.6 |
1.4 |
3.5 |
6.7 |
1.7 |
3.5 |
4.7 |
1.7 |
4.2 |
8.5 |
7.5 |
1.9 |
i=2 |
3.7 |
0.8 |
5.8 |
0.6 |
4.8 |
0.7 |
2.4 |
2.1 |
2.9 |
1.8 |
4.7 |
3.1 |
7.3 |
4.4 |
i=3 |
3.2 |
2.1 |
2.9 |
1.9 |
8.7 |
1.4 |
3.3 |
2.5 |
2.6 |
1.4 |
3.1 |
1.4 |
7.4 |
7.9 |
i=4 |
1.8 |
0.5 |
2.9 |
0.9 |
5.5 |
2.9 |
4.2 |
1.2 |
2.3 |
1.6 |
2.8 |
6.7 |
6.5 |
1.4 |
i=5 |
0.9 |
0.7 |
8.3 |
4.3 |
4.9 |
1.8 |
5.3 |
5.3 |
2.6 |
1.9 |
9.5 |
3.2 |
3.6 |
3.1 |
i=6 |
1.7 |
1.4 |
1.5 |
0.2 |
3.7 |
0.6 |
6.1 |
6.4 |
2.2 |
1.3 |
1.9 |
5.2 |
4.3 |
6.3 |
i=7 |
2.5 |
2.5 |
2.3 |
0.7 |
6.6 |
5.1 |
7.5 |
2.6 |
2.7 |
8.4 |
6.2 |
0.4 |
8.1 |
6.2 |
i=8 |
4.1 |
1.7 |
5.6 |
0.4 |
4.8 |
8.2 |
2.2 |
1.3 |
1.3 |
5.2 |
3.1 |
2.7 |
4.2 |
8.0 |
i=9 |
2.5 |
2.7 |
6.3 |
1.3 |
6.7 |
1.1 |
5.7 |
1.4 |
1.1 |
3.1 |
8.3 |
4.8 |
8.3 |
3.1 |
i=10 |
1.7 |
0.5 |
4.3 |
1.0 |
7.1 |
2.3 |
2.4 |
1.6 |
6.1 |
6.9 |
7.2 |
6.3 |
3.8 |
4.5 |
Т1000 |
1.3 |
2.2 |
3.3 |
2.5 |
2.7 |
3.2 |
2.7 |
2.4 |
1.7 |
6.1 |
7.0 |
2.2 |
2.1 |
3.0 |
Пример выполнения расчетно-графической работы.
Пусть даны значения интенсивностей отказов элементов системы.
Таблица 2.
Значения интенсивностей (1/час) внезапных отказов элементов технической системы.
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
i10-5 |
0.9 |
1.6 |
2.3 |
4.2 |
7.1 |
0.1 |
6.8 |
7.7 |
1.9 |
1.1 |
Т |
3900 час |
|||||||||
Решение.
Интенсивность отказов системы С=33.710-5 1/час.
Ожидаемое время безотказной работы системы ТС=2967.3 час
Для построения функции изменения вероятности безотказной работы системы зададимся интервалом времени от 0 до 5000 часов (более ожидаемого времени безотказной работы системы ТС или заданного времени Т), разобьем этот интервал на равные интервалы и вычислим надежность системы.
Таблица 3
Результаты расчетов надежности технической системы
t (час) |
0 |
1000 |
2000 |
3000 |
4000 |
5000 |
|
1.0 |
0.926 |
0.8572 |
0.7937 |
0.7349 |
0.680 |
PC(t) |
1.0 |
0.7139 |
0.5097 |
0.3638 |
0.2597 |
0.1854 |
|
1.0 |
0.4630 |
0.2144 |
0.099 |
0.046 |
0.021 |
Вероятность безотказной работы системы в течение заданного времени Т=3900 часов равна 0.2687 (Pmax=0.740, Pmin=0.0496).
И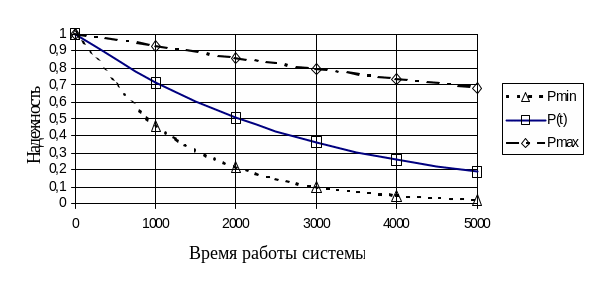
зменение
вероятности безотказной работы системы
во времени согласно (5.14), (5.15), (5.16)
представлено на рис. 1.
Рис.1. Изменение
надежности P(t),
верхней границы
=Pmax
и нижней границы
нерезервированной системы с учетом
только внезапных отказов
Вопросы для самоконтроля.
Сформулируйте основные отличительные особенности технических систем без избыточности.
Выведите формулу определения интенсивности отказов невосстанавливаемой нерезервированной системы.
Какие гипотезы положены в основу определения выражений для оценки надежности технической системы при учете только внезапных отказов элементов.
Приведите формулы расчета надежности, ожидаемого времени безотказной работы системы, интенсивности и частоты ее отказов.
Назовите отличительные особенности оценки надежности нерезервированных технических систем с учетом отказов по износу (старению) элементов.
Объясните принцип определения границ изменения вероятности безотказной работы нерезервированной технической системы.