Лекция № 2. Классификация электромагнитных измерительных преобразователей Преобразование параметров магнитного поля в электрический сигнал

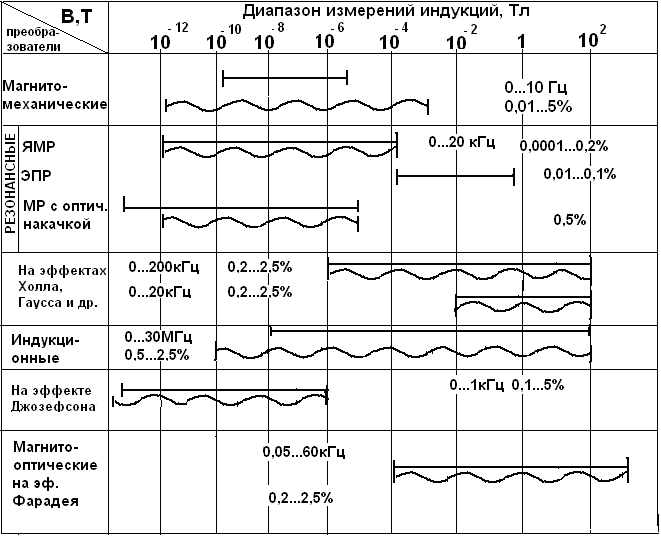
В соответствии с принципом действия и исходными уравнениями электро­магнитные преобразователи могут быть подразделены на следующие большие группы:

1. Преобразователи масштаба тока и напряжения (измеритель­ные трансформаторы тока и напряжения и индуктивные делители напряжения).

2. Электромеханические преобразователи электрического тока в электромагнитную силу. Эти преобразователи используются в элек­тромеханических приборах: амперметрах, вольтметрах, ваттметрах, частотометрах, фазометрах и в качестве обратных преобразователей датчиков уравновешивающего преобразования.

3.Индукционные преобразователи, основанные на законе электромагнитной индукции е = —dΨ/dt и используемые для измерения индукции постоянного и переменного магнитных полей, а также ско­рости.

4. Индуктивные и взаимоиндуктивные преобразователи для измере­ния неэлектрических величин, влияющих на изменение положения отдельных частей преобразователя.

5. Магнитоупругие преобразователи, в которых используется зависимость магнитной проницаемости ферромагнитных материалов от механических напряжений в материале. Применяются для изме­рения сил и давлений.

6. Магнитомодуляционные преобразователи, в которых исполь­зуются нелинейные свойства магнитной цепи.

7. Преобразователи, использующие эффект Баркгаузена. Выход­ной величиной этих преобразователей является ЭДС магнитного шума.

Принцип действия и область применения электромагнитных преобразователей

Электромагнитный (ЭМ) преобразователь представляет собой один или несколько контуров, находящихся в магнитном поле, которое может быть создано как токами, протекающими по контурам, так и внешним источником.

Одноконтурный ЭМ преобразователь характеризуется током i через контур, потокосцеплением Ψ = Li, противо-ЭДС е = - dΨ/dt, энергией электромагнитного поля W_M = Ψi/2 = Li²/2, индуктив­ностью L. Выходной величиной одноконтурного ЭМ преобразова­теля может быть: индуктивность L, электромагнитная сила F_эм и индук­тируемая в контуре ЭДС е_инд.

Индуктивность L = ω² (Re Z_м/z²_м), где ω — число витков кон­тура; Re Z_M и z_M — действительная часть и модуль полного маг­нитного сопротивления

Z_M = ∫ dl_м/(μS_м) пути 1_М, по которому замыкается поток; S_M — поперечное сечение потока; μ — магнитная проницаемость среды, по которой замыкается поток. Индуктивность преобразователя увеличивается, если в магнитное поле контура вво­дится ферромагнитный материал.

ЭМ преобразователь с ферромагнитным сердечником показан на рис. 2.1, а, изменение его индуктивности происходит при изме­нении положения сердечника. Таким образом, входной величиной преобразователя является перемещение. Такой преобразователь на­зывается индуктивным. Изменение индуктивности происходит также при изменении магнитной проницаемости сердечника. Магнитная проницаемость ферромагнитных материалов зависит от значения напряженности магнитного поля в материале. Соответственно индуктивность L зависит от тока, текущего через преобразователь и соз­дающего собственное магнитное поле, и от параметров внешнего маг­нитного поля. Преобразователи, принцип действия которых основан на использовании зависимости L = f(B) называются магнитомодулщионными. При деформации ферромагнетиков также изменяется их магнитная проницаемость. Этот эффект, называемый магнитоупругим, используется в преобразователях для измерения сил и давлений. Принцип действия магнитоупругого преобразователя показан на рис. 2.1, б.

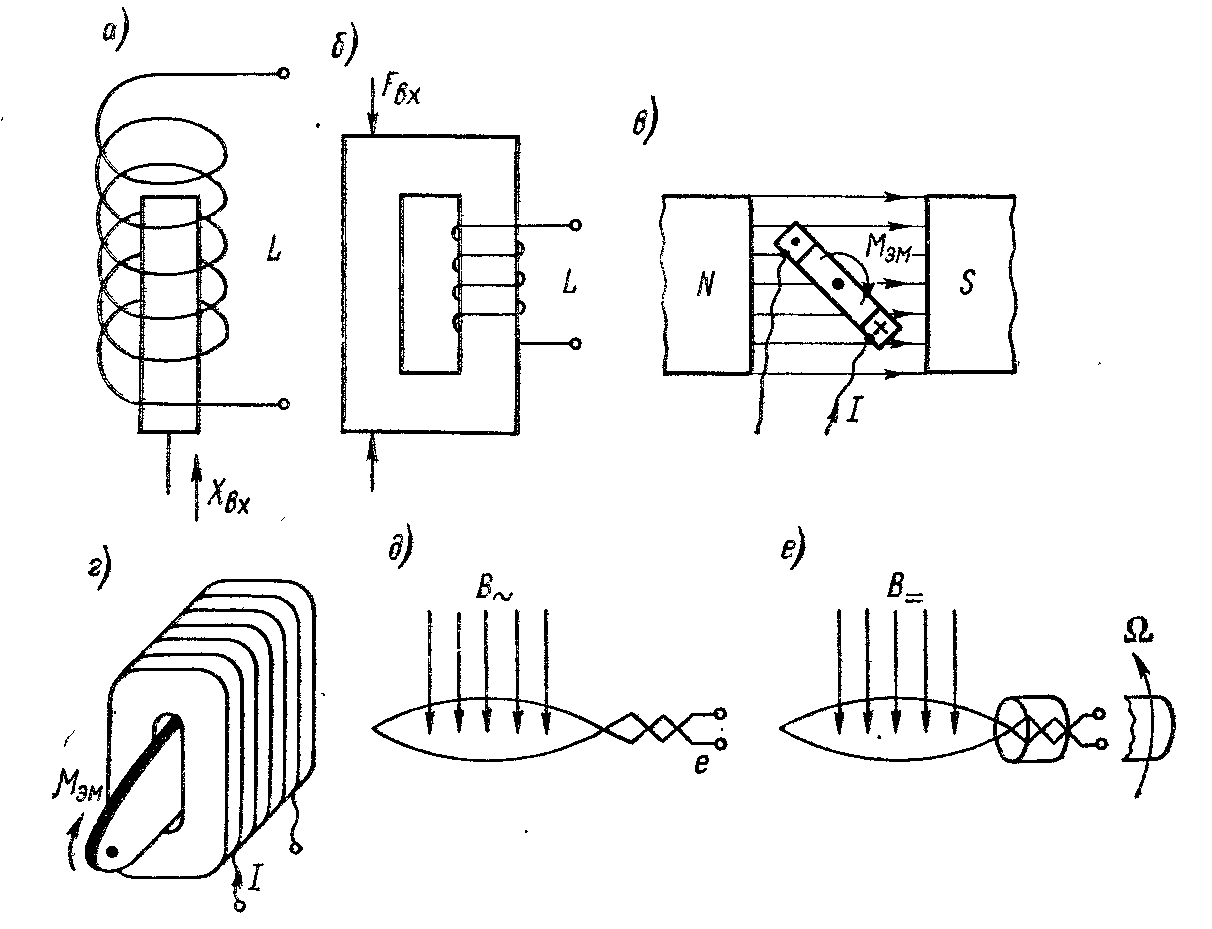
Рис.2.1

Электромагнитная сила действует на контур с током, находя­щийся во внешнем магнитном поле, стремясь сместить или развер­нуть его так, чтобы суммарная индукция магнитного поля была мак­симальной. Эта сила пропорциональна току i и индукции В. Если ток через контур поддерживать постоянным i = const, то по зна­чению электромагнитной силы можно определить индукцию магнит­ного поля В.

Такие преобразователи иногда применяются для измерения маг­нитной индукции. Если, используя постоянный магнит, создать маг­нитное поле с постоянной индукцией В = const, то преобразова­тель может быть применен для преобразования тока в силу и изме­рения тока (рис. 2.1, в). Такие преобразователи называются магнито­электрическими и широко используются в измерительных механизмах электромеханических приборов.

Ферромагнитный сердечник втягивается в контур с током так, чтобы индуктивность контура была максимальной (рис. 2.1, г). В этом случае электромагнитная сила пропорциональна квадрату тока. Подобные преобразователи используются в электромагнитных изме­рительных механизмах электромеханических приборов.

Индуктированная ЭДС е_инд возникает в контуре, находящемся во внешнем магнитном поле, при изменении потокосцепления. Для преобразователя, взаимосвязь которого с внешним магнитным полем характеризуется некоторым обобщенным параметром k при однород­ном внешнем магнитном поле с индукцией В, потокосцепление Ψ = kB и индуктируемая в контуре ЭДС е_инд = —dΨ/dt = — (k∂B/∂t + B∂k/∂t). При неподвижном контуре (∂k/∂t = 0) ЭДС будет индук­тироваться только в переменном магнитном поле. Для контура без сердечника при В = В_т sin ωt ЭДС е = ωSωB_mcos ωt, где ω — число витков и S — площадь контура. Преобразователь, представляющий собой неподвижную катушку (рис. 2.1, д), может быть использован для измерения переменной магнитной индукции. В постоянном маг­нитном поле ЭДС индуктируется только в движущемся контуре, и для измерения индукции В контуру задают принудительное движе­ние, например вращение с постоянной скоростью, как показано на рис. 2.1, е. Можно использовать преобразователь и для решения обратной задачи — определения по значению выходной ЭДС ско­рости при движении контура в поле с известной индукцией B_N. Пре­образователи, выходной величиной которых является ЭДС е_инд, назы­ваются индукционными.

ЭМ преобразователи строятся таким образом, чтобы выделить зависимость между входной величиной и одной из перечисленных выходных величин, однако учитывать в большинстве преобразовате­лей приходится проявление всех взаимосвязей. Так, на сердечник преобразователя (рис. 2.1, а) действует электромагнитная сила, которая может вызвать дополнительное перемещение сердечника, т. е. помеху, искажающую входную величину. На контур, в котором наводится ЭДС е_инд (рис. 2.1, д), если он замкнут на конечное сопро­тивление и по нему протекает ток, действует сила, стремящаяся опре­деленным образом ориентировать его относительно поля. Поворот контура под действием этой силы вызовет изменение индуктируемой ЭДС.

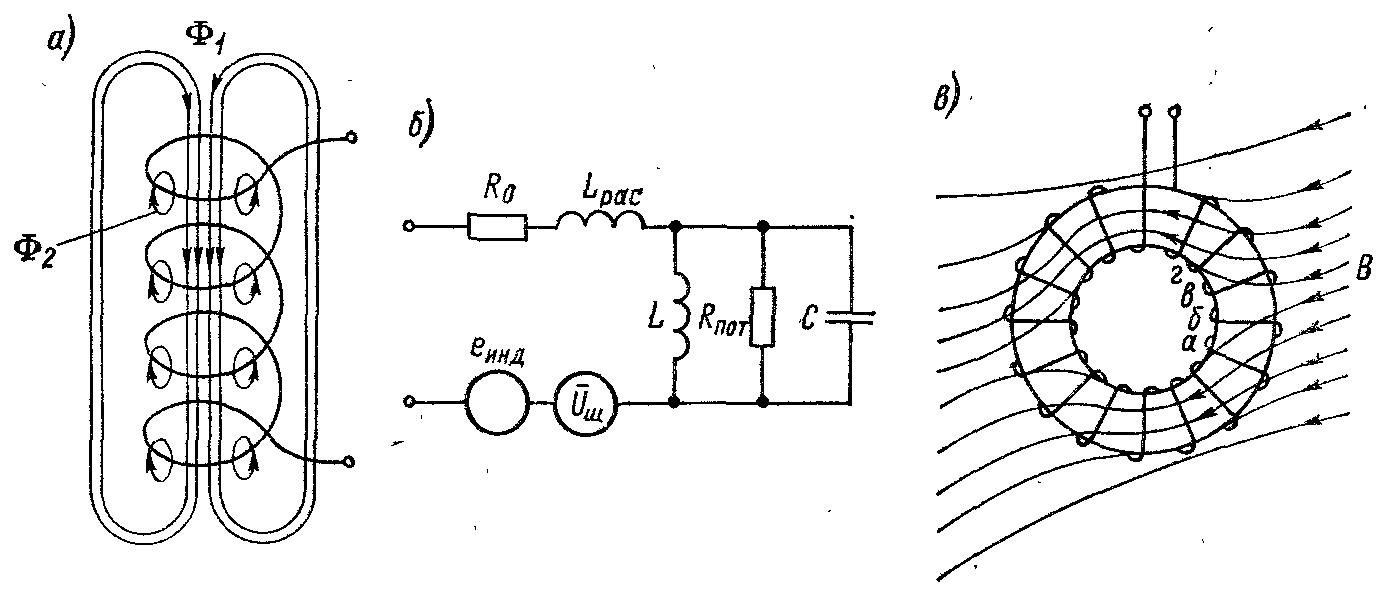Рис.2.2

Эквивалентная схема одноконтурного ЭМ преобразователя. Пре­образователь с контуром в виде обмотки, содержащей ω витков, показан на рис. 2.2, а. Основной поток Ф₁ контура пронизывает всю обмотку и сцепляется со всеми витками. Однако некоторая часть потока Ф₂, называемая потоком рассеяния, замыкается, не пронизывая ряд витков. Соответственно полная индуктивность контура имеет две составляющие: основную индуктивность L=ω²/Z_M и индуктивность рассеяния L_pac = ω/Z'_M, где Z_M и Z'_М — магнитные сопротивления основного потока и потока рассеяния. Если в обмотку преобразователя введем ферромагнитный сердечник, в котором кон­центрируется магнитный поток, то доля потоков рассеяния в общем потоке уменьшается и отношение L/L_pac увеличивается. Наименьшую индуктивность рассеяния имеет обмотка, выполненная на тороидаль­ном сердечнике.

Однако при введении ферромагнетика появляются зависящие от частоты потери мощности на перемагничивание магнитопровода. Эти потери учитываются сопротивлением R_пот, включенным парал­лельно индуктивности L. Кроме того, в эквивалентной схеме должны быть учтены также межвитковые емкости; в области частот до 10³— 10⁴ Гц они учитываются в виде сосредоточенной емкости.

Эквивалентная схема преобразователя, в которой учтены сопро­тивление обмотки постоянному току R_o, основная индуктивность L, индуктивность рассеяния L_pac, емкость С и сопротивление потерь R_пот, приведена на рис. 2.2, б. В ней учтены также источники ЭДС е_инд и U_ш, которые характерны для ЭМ преобразователей. ЭДС е_инд индук­тируется в контуре, находящемся во внешнем магнитном поле. Эта ЭДС может быть информативной, как в индукционном преобразова­теле, но может являться и помехой. Для того чтобы уменьшить ту со­ставляющую е_инд, которая является помехой, преобразователи экра­нируются от внешнего магнитного поля, соединительные провода под­водятся таким образом, чтобы не образовывать дополнительных контуров (см. рис. 2.1, д). Преобразователи, находящиеся в магнит­ных полях, защищаются от механических помех (вибрации, акусти­ческие воздействия), вызывающих колебания частей преобразователя и наведение ЭДС.

Уменьшить составляющую помехи е'_инд можно, применяя в пре­образователях симметричные магнитные цепи и симметричные обмотки. В качестве примера на рис. 2.2, в показана магнитная цепь в виде тороидального сердечника. При равномерной обмотке для каждого витка есть симметрично расположенный по отношению к магнитному потоку, пронизывающему тор, парный виток (например, витки б и в или а и г). ЭДС, наводимые в «парных» витках, компенсируют друг друга, и суммарная ЭДС е'_инд при идеальной симметрии равна нулю.

В высокочувствительных ЭМ преобразователях с ферромагнитным сердечником иногда приходится считаться с напряжением шума, обусловленным в области средних частот главным образом эффектом Баркгаузена, т. е. импульсами ЭДС, вызываемыми скачкообраз­ными смещениями доменных границ при перемагничивании ферромагнетика. Эффект Баркгаузена используется также при построе­нии ряда преобразователей. Известно, что фер­ромагнетики состоят из большого числа элементарных областей (доменов), объем которых для разных типов ферромагнетиков составляет 10^-3 — 10^-6 мм³. Векторы намагниченности доменов ориенти­рованы таким образом, что при отсутствии внешнего магнитного поля намагниченность образца в целом равна нулю. При наложении внешнего магнитного поля элементарные области перемагничиваются. Переориентация доменов может происходить скачками, при этом в витках обмотки ин­дуктируются импульсы ЭДС е = -∆Ф/τ где ∆Ф — приращение маг­нитного потока, вызван­ное скачком Баркгау­зена; τ — длительность скачка. Длительность скачков Баркгаузена со­ставляет для разных ма­териалов 10^-3 — 10^-7 с.

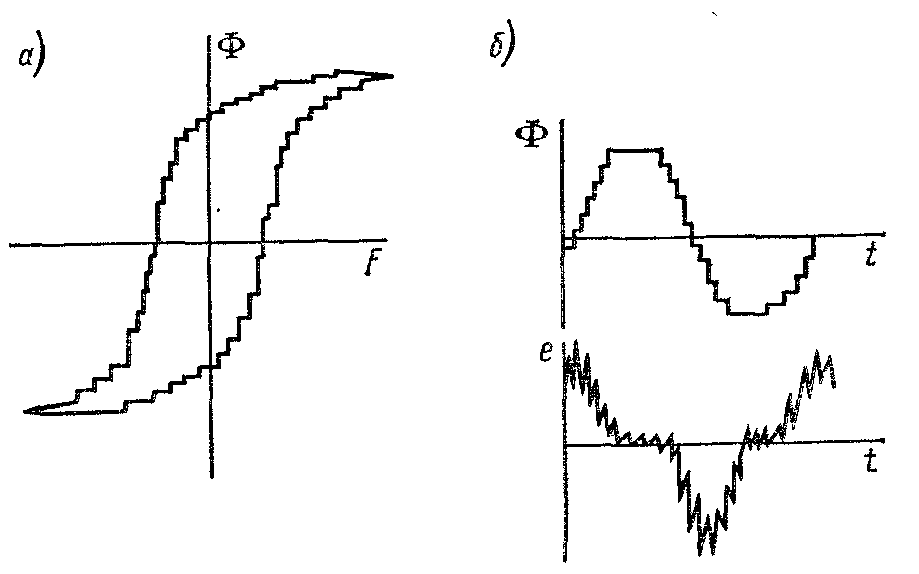
Рис.2.3

На рис. 2.3, а по­казан гистерезисный цикл со скачками Барк­гаузена (масштаб скачков сильно увеличен, и они характеризуют процесс лишь с качественной стороны), на рис.2.3,б изображена кривая магнитного потока Ф=f(t) и кривая ЭДС е=φ(t). Ступеньки на кривой намагничивания неодинаковы по величине и меняют свое положение от цикла к циклу перемагничивания, магнитный шум является случайным процессом. Верхняя граница распределения f₂ определяется длительностью скачков Баркгаузена и составляет 10²— 10⁶ Гц, в ферритах f₂ может достигать 10⁷ Гц. Нижняя граница f₁ зависит от частоты перемагничивания f₀ и составляет не менее f₁ =3f₀

ЭДС, вызываемая магнитным шумом, включается в эквивалентную схему ЭМ преобразователя (рис. 2.2, б). Однако, как правило, ЭДС U_ш оказывается значительно меньше других помех, в частности е_инд; поэтому с наличием U_ш приходится считаться только в высокочув­ствительных преобразователях магнитных величин (феррозонды), в магнитных и параметрических усилителях.

Двухконтурный ЭМ преобразователь схематично показан на рис. 2.4. Преобразователи, содержащие два или несколько контуров, называют трансформаторными или взаимоиндуктивными. Если про­пустить переменный ток через контур 1, то в контуре 2 будет индук­тироваться ЭДС, зависящая от угла α между плоскостями контуров и максимальная при совпадении этих плоскостей (рис. 8-4, а). Поток, с которым сцепляется контур 2 при прохождении тока по кон­туру 1, равен Ψ₂ = М₁₂i₁ где М₁₂ = ω₁ ω₂ Re Z_M/z_M — взаимоин­дуктивность контуров; ω₁ и ω₂ - числа витков контуров; Z_M — маг­нитное сопротивление пути, по которому замыкается поток между контурами.

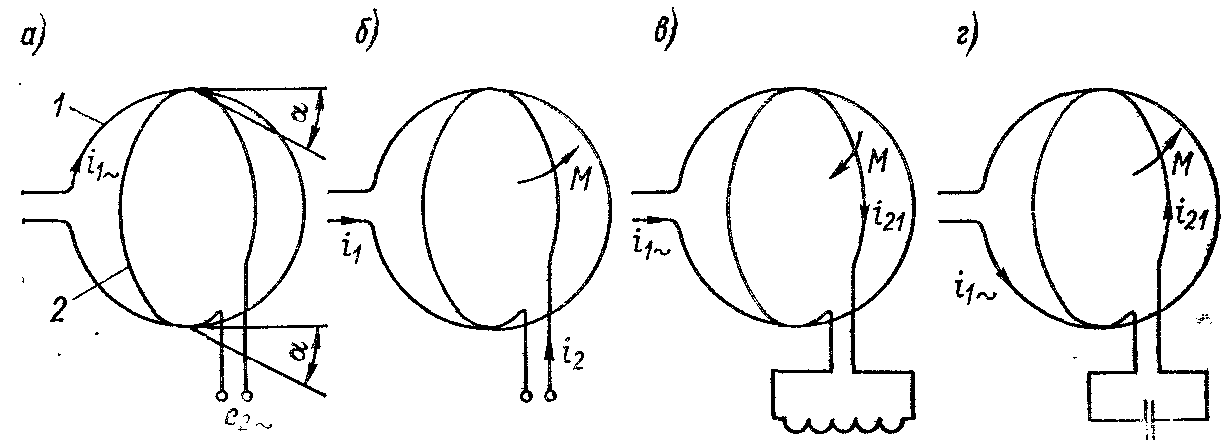
Рис. 2.4

При пропускании токов i₁ и i ₂ через оба контура между ними возникает механический электромагнитный момент М, стремящийся развернуть их так, чтобы магнитное поле было максимальным, т. е. чтобы плоскости контуров совпали (рис. 2.4, б). При этом если токи i₁ и i₂ переменные, то в образовании момента могут участвовать не только токи, создаваемые внешними источниками, но и токи i₁₂ и i₂₁, наводимые в каждом из контуров потоком соседнего контура. При чисто активном сопротивлении контура момент равен нулю, так как между наводящим потоком и наведенным током фазовый сдвиг составляет 90°. Если же кон­тур замкнуть на индуктивное или емкостное сопротивление, то развивае­мый момент будет максимальным и кон­тур будет стремиться развернуться так, как показано на рис. 2.4, в и г.

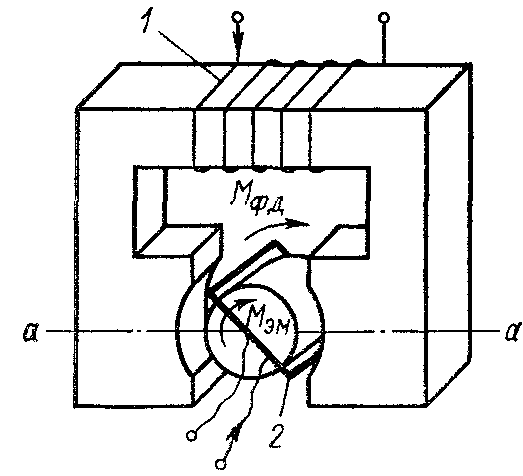
Рис. 2.5

Для того чтобы усилить электромаг­нитное поле и сконцентрировать его в определенной области, применяют фер­ромагнитные магнитопроводы. Пример двухконтурного преобразователя с фер­ромагнитным сердечником показан на рис. 2.5. Если через обмотку 1 прохо­дит переменный ток, то в рамке 2 наводится ЭДС, зависящая от угла поворота рамки и максимальная, когда плоскость рамки перпендикулярна линии а — а. Если ток пропустить и через рамку 2, то на рамку будет воздействовать момент М_фд, стремящийся повер­нуть ее так, чтобы магнитное поле рамки совпало с магнитным полем обмотки. На короткозамкнутую рамку также воздействует момент М_инд, вызываемый индуктированным в рамке током. Кроме того, между обмотками и ферромагнитным магнитопроводом действует электромагнитная сила или момент, стремящиеся расположить их так, чтобы магнитный поток, создаваемый соответствующей обмоткой, был мак­симальным. В примере на рис. 2.5 обмотка 1 оптимальным образом расположена относительно магнитопровода, поэтому между ней и. магнитопроводом такая сила не возникает; рамка 2 должна быть развернута так, чтобы ее плоскость была перпендикулярна линии а — а. Однако момент М_эм, направление которого показано на рис. 2.5, очень мал по значению, так как изменение магнитного поля рамки 2 мало зависит от ее поворота относительно магнитопровода.

Энергия электромагнитного поля определяется формулой

(2.1)

Учитывая, как показано выше, что в преобразователе могут дей­ствовать, кроме потоков самоиндукции Ψ_L = i_kL_k, потоки взаимо­индукции Ψ_M = i_pM_kp и потоки внешнего поля Ψ_kвнеш, а токи в каждом из контуров, кроме составляющей тока от внешнего источ­ника i_k0, могут содержать еще и ток i_kΨ, наведенный потоком Ψ, выражение для энергии первого контура можно представить состоя­щим из нескольких членов:

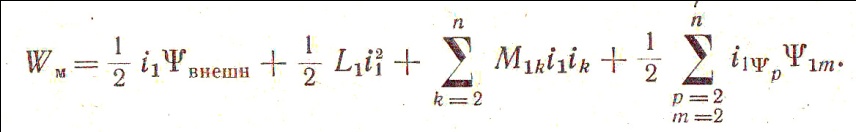(2.2)

Электромагнитная сила, действующая на первый контур, в соот­ветствии с выражением энергии может иметь четыре составляющие f_мэ, f_эм, f_эд и f_инд, называемые соответственно магнитоэлектрической, электромагнитной, электродинамической и индукционной:

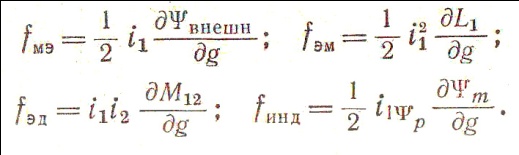(2.3)

Характер изменения соответствующих сил во времени при синусоидальном входном токе показан на рис. 2.6, а — д. Из рисунка видно, что при постоянном потоке Ψ_внеш сила f_мэ пропорциональ­на мгновенному току, сила f_эм имеет постоянную составляющую, пропорциональную квадрату действующего тока, F_эм= 1/2I²∂L/∂g и переменную составляющую, являющуюся второй гармоникой. Сила f_эд имеет постоянную составляющую F_эд = I₁ I₂ cos (I₁ ^ I₂) ∂M₁₂/∂g, пропорциональную произведению токов и косинусу угла между их век­торами, и переменную составляющую, также зависящую от угла сдвига между токами. На рис. 2.6, г показан характер силы f_эд, если токи имеют разную частоту.

Характер силы f_инд зависит от сдвига между током в контуре и взаимодействующим с ним потоком Ψ_m. Сила f_инд также имеет постоянную и переменную составляющие, особенностью которых явля­ется зависимость от частоты потока Ψ_P, наводящего ток в контуре, так как чем выше частота, тем больше ток i_1Ψp=(∂ Ψp /∂l)* (1/Z₁ ).

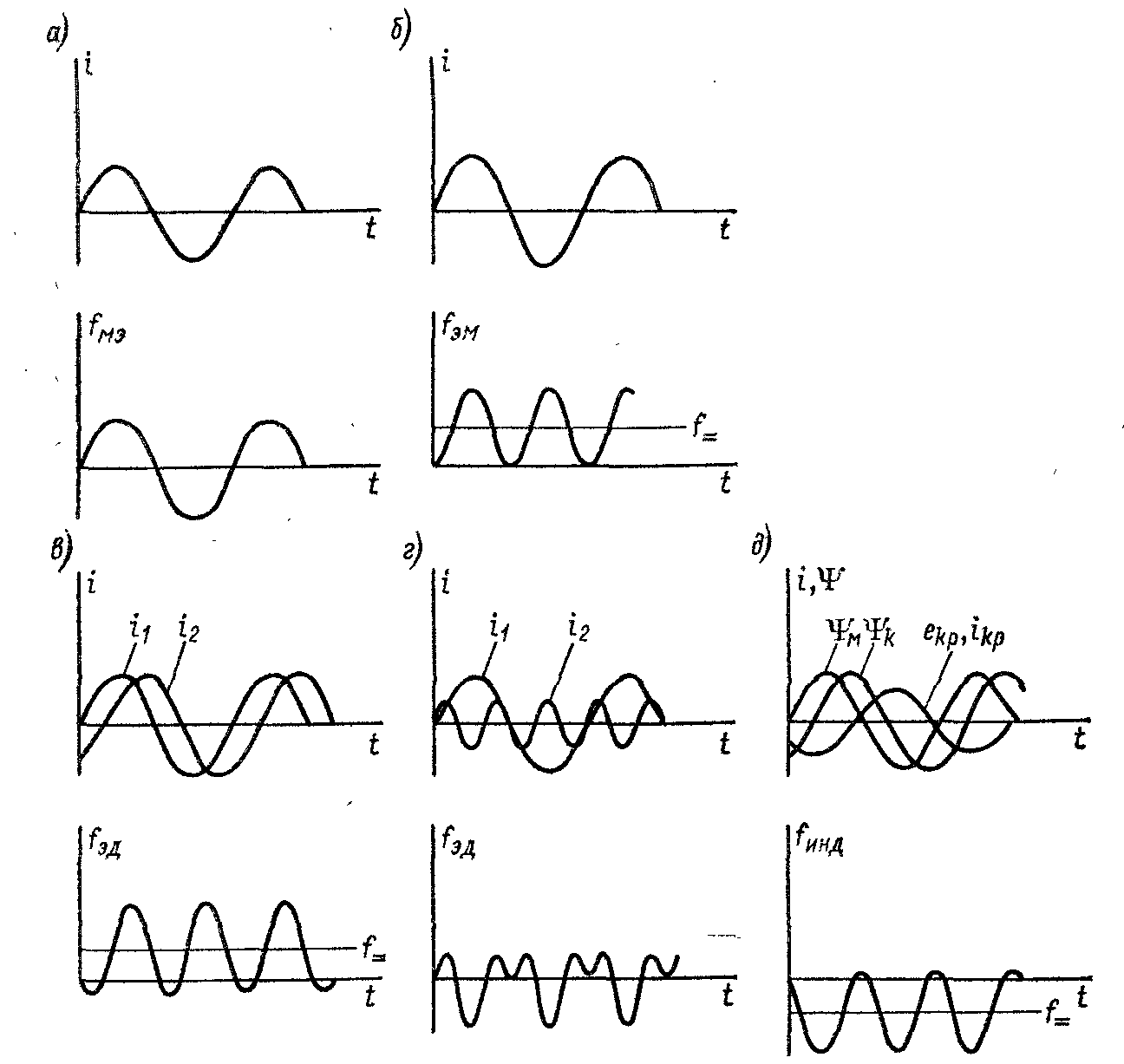Рис. 2.6

Погрешности

Суммарная погрешность прибора может быть выражена в виде абсолютной погрешности ∆B_0i или в виде приведенной относительной погрешности δ = B_0i / B_пред.

Большое практическое значение для минимизации суммарной погрешности при проектировании прибора, изготовлении и настройке имеет влияние ее мультипликативных и аддитивных составляющих.

Мультипликативными составляющими погрешности называют такие составляющие, которые максимально или иначе зависят от значения и направления вектора измеряемого поля B_0.

Аддитивными составляющими погрешности называют такие составляющие, которые не зависят от вектора B_0.

Разделяют их потому, что существуют способы их минимизации.

Уравнение преобразования для магнитометра постоянных полей имеет вид:

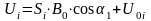(2.4)

где U – выходное напряжение, поступающее на РУ;

S – коэффициент преобразования;

В₀ – значение (модуль) вектора измеряемого поля;

α – угол между вектором измеряемого поля В₀ и магнитной осью феррозонда.

U₀ – напряжение, характеризующее смещенный нуль (сдвиг) и шум канала.

При суммарная погрешность по входу составляет:

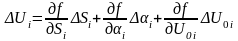(2.5)

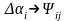,причем ψ_ij и U₀ малы.

Применительно к трехкомпонентному магнитометру:

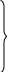
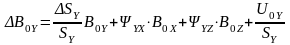(2.6)

Первые 3 члена в правой части каждой строки – мультипликативные составляющие погрешности. Последние – аддитивные составляющие.

Формула (2.6) применяется тогда, когда отклонения от номинальных значений носят систематический характер. Если же эти отклонения – случайные величины, то пользуются следующей формулой:

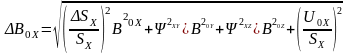
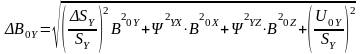(2.7)

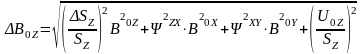
При измерении относительно сильных магнитных полей доминирующими оказываются мультипликативные погрешности, а аддитивной погрешностью можно пренебречь. При измерении же слабых магнитных полей на первый план выходят аддитивные погрешности.

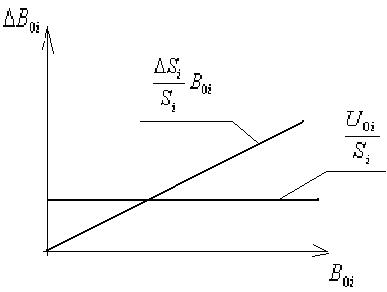
Способы минимизации мультипликативных погрешностей

Мультипликативная погрешность, вызванная отклонением ∆S_i коэффициента преобразования S_i от своего номинального значения S^* (∆S_i = S_i - S^*)пропорциональна значению измеряемой составляющей поля В_0i. Можно уменьшить эту погрешность за счет уравновешивания составляющей поля В_0i в объеме феррозонда.

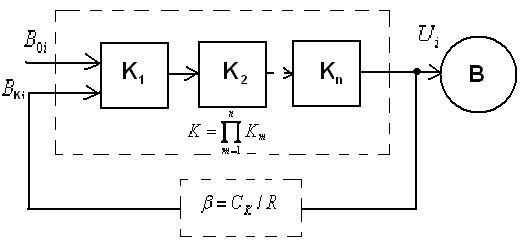
Уравновешивание осуществляется путем подачи тока в катушку компенсации, надетую на феррозонд.

В первой схеме ток компенсации формируют цепью обратной связи.

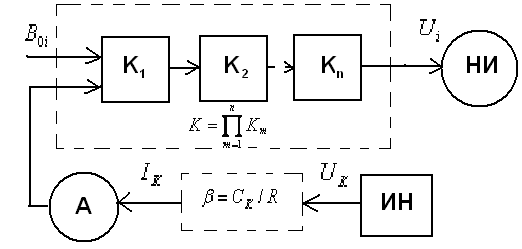
Во второй – ток подают от автономного источника, устанавливая момент компенсации по нуль-индикатору НИ.

k-цепь – цепь прямого преобразования.

β-цепь – цепь обратного преобразования.

Минимизация погрешности в 1 схеме достигается при условии:

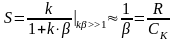(2.8)

где 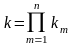- коэффициент прямого преобразования;

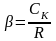- коэффициент обратного преобразования;

С_К – постоянная катушки компенсации;

R – суммарное сопротивление цепи обратной связи.

- если регистрации подлежит выходное напряжение U_вых.

Если же регистрации подлежит ток обратной связи, то относительная погрешность коэффициента преобразования будет

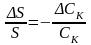(определяется погрешностью постоянной катушки компенсации)

Минимизация мультипликативной погрешности во второй схеме достигается при условии

B_0i = - B_ki (2.9)

где B_ki – поле компенсации.

В этом случае k-цепь выполняет роль нуль-индикаторной цепи, непосредственной регистрации подлежит напряжение или ток в β-цепи, следовательно, и погрешности вносятся элементами этой цепи.

Формулы аналогичные.

К приемам минимизации мультипликативных погрешностей также относятся:

• выбор сердечников с наименьшей поперечной проницаемостью;

• жесткое закрепление всех элементов феррозонда и обеспечение минимального угла непараллельности между продольной осью сердечника и осью ИК;

• стабилизация амплитуды (или максимального значения поля возбуждения)

Способы минимизации аддитивных погрешностей

Следствием аддитивных погрешностей является внутренние и внешние помехи, воздействующие на различные элементы канала магнитометра.

Предположим, что помеха в виде ложного напряжения U^л_p действует на входе p-го элемента канала магнитометра. Тогда ложный сигнал на выходе канала с обратной связью:

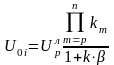(2.10)

Отсюда аддитивная погрешность имеет вид:

(2.11)

Отсюда, в каком бы элементе канала не содержался источник ложного сигнала, значение приведенной ко входу аддитивной погрешности от глубины обратной связи не зависит. Поэтому основным способом минимизации аддитивной погрешности является выявление и возможное устранение самих источников этих погрешностей.

1. В электронной части прибора основным источником аддитивной погрешности является ГВ, вырабатывающий напряжение (ток) не только основной частоты f и нечетных гармоник (2n+1)f, но и четных 2nf.

Общими и достаточно эффективными приемами уменьшения и подавления четных гармоник напряжения генератора являются:

• выбор такого режима работы всех его усилительных элементов, при котором нелинейные искажения становятся линейными;

• построение генератора по двухконтактной схеме с элементами ее симметрирования.

Все современные генераторы содержат задающий каскад с кварцевым резонатором, обеспечивающим высокую стабильность частоты.

2. Основная частота и нечетные гармоники напряжения небаланса феррозонда, попадая на вход избирательного усилителя, вызывают в нем появление четных гармоник напряжения, а, следовательно, и ложного сигнала. Способы подавления ложных четных гармоник напряжения в ИУ те же, что и в генераторах.

3. СД и УПТ также вырабатывают ложные сигналы, но уже в виде постоянных напряжений. В схеме при «закорачивании» входа СД (при отключении выхода ИУ). Наименьший уровень ложного сигнала обеспечивают синхронны датчики, собранные по двухпериодной схеме на полевых транзисторах, а усилители постоянного тока – на основе операционных усилителей.