4.3. Сообщающиеся сосуды

Пусть в сообщающиеся сосуды залиты две несмешиваю­щиеся жидкости с плотностями p₁ и р₂ (рис. 4.3).

Установим условие равновесия жидкости при давлениях в сосудах над жидкостями p₁ и р₂. Предельное верхнее по­ложение поверхности уровня для двух сообщающихся сосу­дов показано на рис. Здесь p = const, т. е. р_а=р_В, где p_А = P ; p_B= .

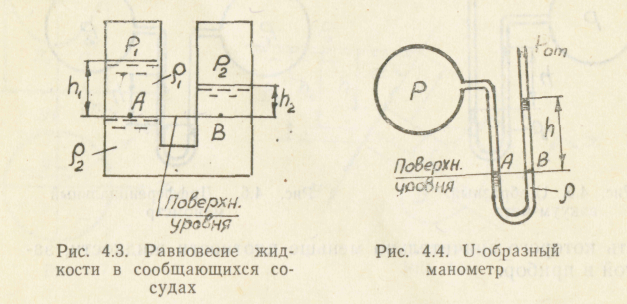
Тогда условие равновесия можно записать в виде

.

Принцип сообщающихся сосудов часто применяется в из­мерительной технике. Прибор, изображенный на рис. 4.4, называется U-образным манометром.

Так как р_А = р_в или p=p + , то перепад уровней жидкости в трубках прибора составит h = (p—Рат)/( ), т. е. прибор измеряет избыточное давление над атмосферным или манометрическое давление.

Если pp_ат, то уровни жидкости в трубках приборах установятся так, как показано на рис. 4.5. В этом случае h=(p_ат—p)/(pg),

т. е. прибор измеряет вакуум или давление, не достающее до атмосферного.

Прибор, показанный на рис. 4.6, называется дифференци­альным манометром (дифманометром). Он измеряет раз­ность давлений в двух сравниваемых точках:

h = (p₁— p₂)/(g).

Во всех приведенных примерах предполагалось, что в со­судах, давление в которых измерялось, находился газ, плотность

которого значительно меньше плотности жидкости, за­литой в прибор.

4.4. Равновесие жидкости в центробежном поле

На жидкостные частицы, находящиеся во вращающемся с постоянной скоростью вокруг вертикальной оси цилиндри­ческом стакане, действуют сила тяжести mg центробежная сила (рис. 4.7). Следовательно, в этом случае

X=²rcos(r, x); Y=²rcos(r, y); Z=g

Или

X=²x; Y=²y.

Подставим эти выражения в (4.3) и проинтегрируем по­следнее. Получим

(4.10)

или

(4.11)

При р = const уравнение (4.10) преобразуется в уравне­ние поверхности уровня-—уравнение параболоида вращения. Постоянную интегрирования С в (4.11) найдем из началь­ного условия р = р₀ при r = 0 и z=z₀..

Тогда

.

4.5. Сила давления на плоскую поверхность тела

Силы давления, действующие на каждый элемент поверх­ности ds (рис. 4.8), параллельны, т.е. суммирование их мож­но проводить алгебраически:

(4.12)

и результирующая сила Р всегда направлена по внутренней нормали к плоской поверхности. Подставим (4.9) в (4.12). С учетом того, что h= ysina, получим

.

Статический момент площади s относительно оси х мож­но записать в виде ,

где точка С — центр тяжести площади s. Поскольку y_csin=h_c, то

Р =Р₀+P (4.13)

где Po=p₀s,

, (4.14)

т. е. для вычисления величины равнодействующей силы дав­ления необходимо знать давление р_с в центре тяжести пло­щади.

Найдем точку приложения равнодействующей силы дав­ления. Очевидно, что составляющая ее P₀=p₀s приложена в точке С. Для определения центра давления (точки D) со­ставляющей Р_Г составим уравнение моментов сил относитель­но оси х:

или, т.к. P_Г=gh_cs и h=ysin, то

, (4.15)

где I_ох — момент инерции площади s относительно оси х. Поскольку I_0X=I_C+ , то после подстановки этого вы­ражения в (4.15) получим

,

где I_с — момент инерции площади относительно горизонталь­ной оси, проходящей через центр тяжести площади.