4. Гидростатика

4.1. Основное уравнение гидростатики (уравнение Эйлера)

В состоянии покоя скорость жидкости u=0. В этом слу­чае уравнения (3.10) и (3.10') соответственно примут вид

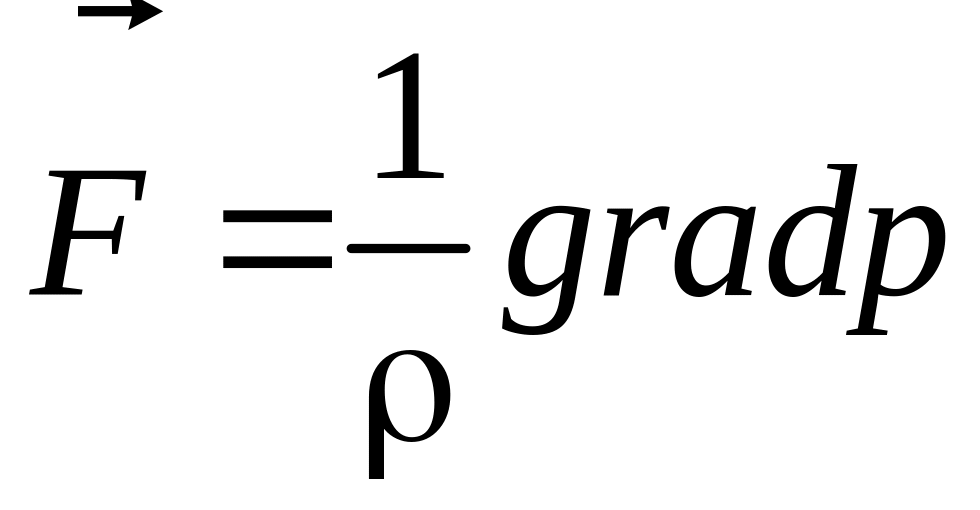(4.1)

и

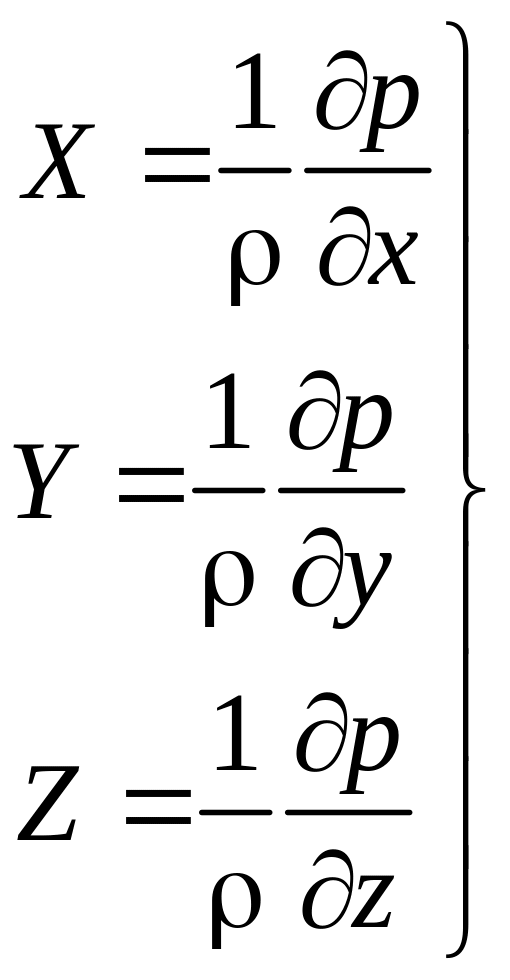(4.1’)

Уравнение (4.1) или (4.1’) — уравнение Эйлера.

Выясним, при каких условиях жидкость может находить­ся в равновесии. Для этого умножим построчно уравнения (4. 1’) на dx, du, dz и просуммируем их:

. (4.2)

Поскольку р=р (х, у, z), то выражение в круглых скобках есть полный дифференциал давления dp. Если =const, то

правая часть (4.2) равна или

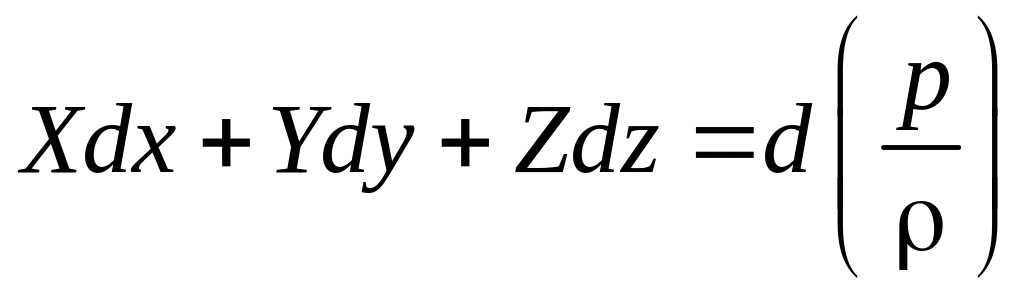. (4.3)

Уравнение (4.3) имеет решение всегда, т. е. жидкость мо­жет находиться в равновесии, если левая часть уравнения (4.3) представляет собой полный дифференциал некоторой функции Ф, зависящей от х, у, z. Так как

, (4.4)

то, сравнив (4.3) и (4.4), легко установить условия, при ко­торых жидкость может находиться в равновесии:

(4.5)

Массовые силы, обладающие свойством (4.5), называют­ся силами, имеющими потенциал, а функция Ф — потенци­альной. Итак, жидкость может находиться в равновесии только в потенциальном силовом поле. Напомним, что рабо­та сил, имеющих потенциал, равна разности потенциалов:

,

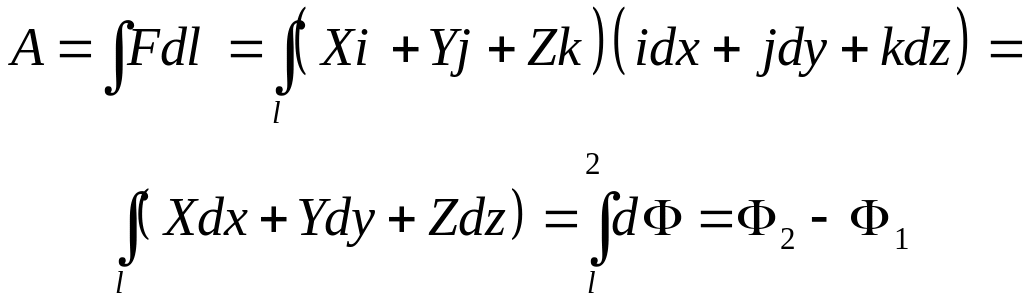где Ф₁ и Ф₂ — значения потенциалов в конечных точках пути l.

Поверхность, на которой Ф = const или dФ=0, называет­ся эквипотенциальной или поверхностью уровня. На этой по­верхности (4.3) dp =0 или р =const или

Xdx+Ydy+Zdz=0. (4.6)

Поясним применение основного уравнения гидростатики на конкретных примерах.

4.2. Равновесие жидкости в гравитационном поле

На жидкостные частицы с массой т действует сила тяже­сти G=gm, т. е. F=G/m=g. Следовательно, (рис. 4.1)

Z = – g; X = Y = 0. (4.7)

Уравнение поверхности уровня примет вид – gdz = 0 или после интегрирования

z = const,

т. е. поверхность уровня представляет собой горизонтальную плоскость. После интегрирования уравнения (4.3) с учетом (4.7) получим

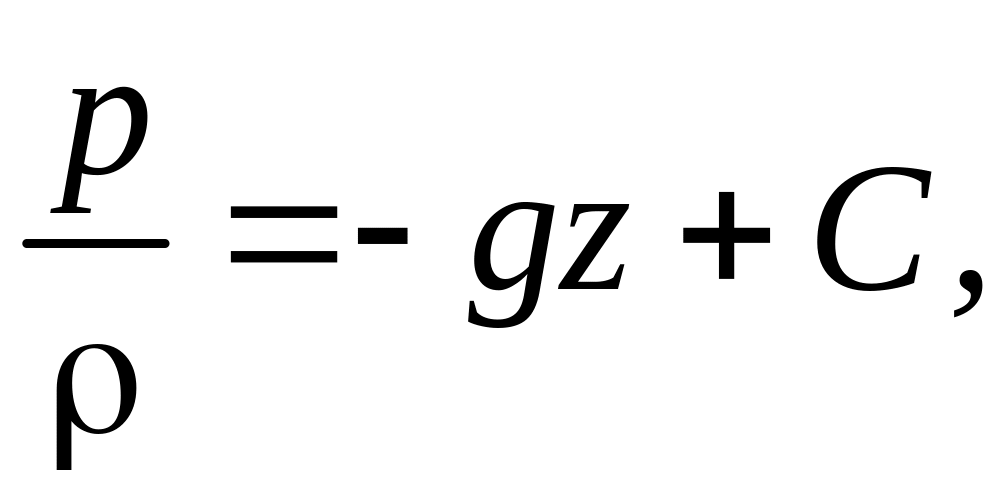
или

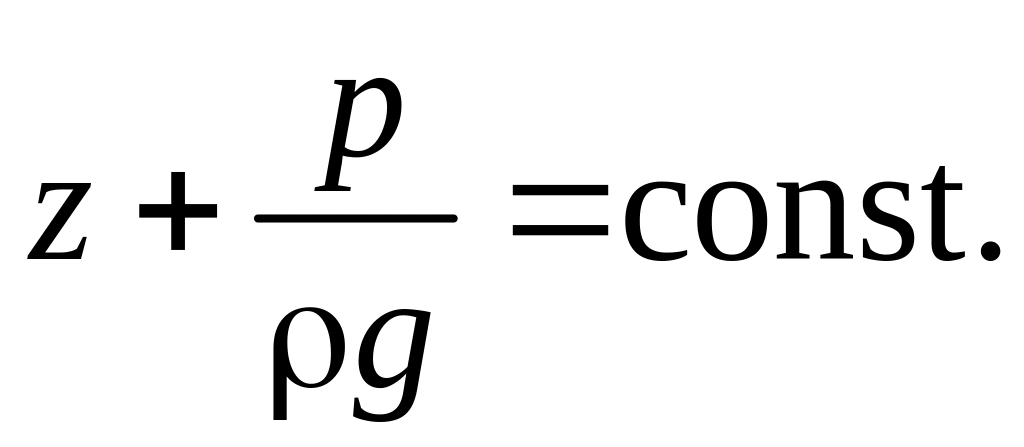(4.8)

Постоянную интегрирования С найдем из начального ус­ловия р=р₀ при z=z₀. Тогда и

p=p₀ + g (z₀-z) =p₀+ gh, (4.9)

где h=z₀ - z — глубина погружения точки под поверхностью уровня с известным давлением р₀.

Частным случаем поверхности уровня является свободная поверхность жидкости, т. е. можно принимать в качестве р₀ давление над свободной поверхностью жидкости, a h — глу­бину погружения точки под свободной поверхностью жидко­сти. В этом случае второе слагаемое в (4.9) gh называется избыточным гидростатическим давлением.

Графическое изображение распределения давления по по­верхности тела называется эпюрой давления (рис. 4.2).

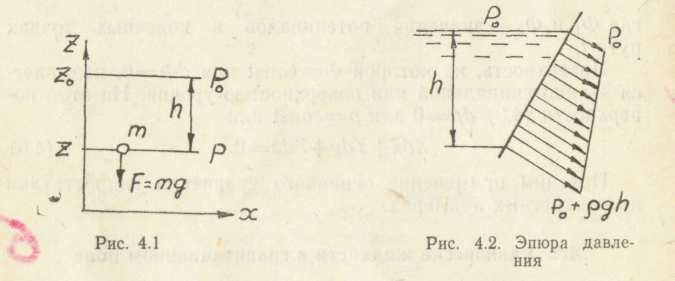
Уравнение (4.8) имеет простой энергетический смысл.

Первое слагаемое можно представить в виде z= mgz/(mg)=Э_n/(mg), т. е. z есть отношение потенциаль­ной энергии положения к весу жидкостной частицы с мас­сой т. Второе слагаемое также характеризует потенциаль­ную энергию, так как численно равно высоте, на которую поднимается жидкостная частица под действием давления р. Итак, слагаемые уравнения (4.8) можно назвать: z — удель­ная потенциальная энергия положения; p/(g)—удельная потенциальная энергия давления (сумму z+p/( )—иногда называют «статический напор»). В такой интерпретации уравнение (4.8) эквивалентно утверждению: в покоящейся жидкости все частицы обладают одинаковой энергией.