2. Элементы кинематики жидкости

Скорость жидкости может быть задана двумя способами. Первый из них (метод Лагранжа), наиболее естественный, предполагает известными траектории движения каждой жидкостной частицы, имеющей в начальный момент времени координаты r₀ или (а, b, с); или х=х(а, b, с, t); у=у(а, b, с, t); z=z(a, b, с, t). Переменные или а, b, с называются переменными Лагранжа. В этом случае мгновенную скорость можно вычислить так:

Отметим, что этот метод описания движения жидкости не получил широкого применения из-за сложности получаемых уравнений движения.

Второй метод (метод Эйлера) заключается в непосредственном описании поля скоростей в пространстве и времени: или u_x=u_x(x,y,z,t); u_y=u_y(x,y,z,t); и = u_z(x, у, z, t).

Этот метод получил преимущественное применение.

Движение называется установившимся или стационарным, если скорость в каждой точке пространства не изменяется во времени (например, истечение жидкости из отверстия в днище сосуда при постоянном уровне жидкости). Если же скорость изменяется во времени, то движение называется неустановившимся или нестационарным.

Линия тока — это линия, в каждой точке которой в данный момент времени вектор скорости и направлен по касательной (рис. 2.1). Из определения следует, что , т. е. их векторное произведение , или так как , a , то , или

(2.1)

Уравнение (2.1)—это дифференциальное уравнение линии тока.

Траектория — линия, по которой материальная точка перемещается в пространстве во времени. За время dt точка пройдет путь . В проекции на оси координат или

(2.2)

Уравнение (2.2) — дифференциальное уравнение траектории по форме совпадает с уравнением для линии тока (2.1). Однако решения их различны: при нахождении уравнения линии тока интегрирование уравнения необходимо проводить для данного момента времени t=const. Линия тока и траектория совпадают при установившемся движении жидкости.

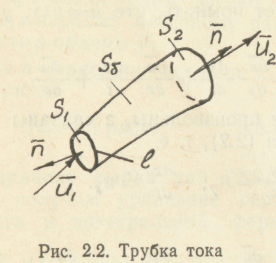
Трубка тока. Через каждую точку произвольного контура l проведем линии тока (рис. 2.2). Полученная трубчатая поверхность называется трубкой тока. Если контур l мал, то трубка тока называется элементарной.

Объемный расход жидкости через произвольное сечение ds с нормалью элементарной трубки тока (рис. 2.3) вычислим из простых рассуждений: объем жидкости, протекший

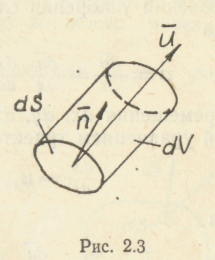
через сечение ds за время dt, равен объему цилиндра , т. е. расход

(2.3)

где и_п — проекция на нормаль ; — площадь сечения, перпендикулярная линиям тока, или «живое сечение».

По аналогии массовый расход жидкости в элементарной трубке тока

(2.4)

Расход жидкости через произвольную площадку s можно вычислить, просуммировав расходы по элементарным пронизывающим ее трубкам, т. е. объемный расход

(2.5’)

массовый расход

(2.5)

Размерность: [Q] = м³/c; [G]=кг/с.

Средняя расходная скорость v в живом сечении s_n связана с объемным расходом соотношением

Q = vs_n. (2.6)

Ускорение при движении жидкости вычисляется по формуле

Если известно поле скоростей (по методу Эйлера), то при вычислении ускорения следует помнить, что и—и (х, у, z, t). Тогда

а переменные dx, dy,dz не произвольны, а связаны между собой уравнением траектории (2.2), т. е.

Итак,

(2.7)

Составляющая ускорения — называется локальным ускорением, она характеризует изменение скорости в данной точке пространства. Очевидно, что при установившемся движении . Сумма слагаемых — называется конвективным ускорением, она ха­рактеризует изменение скорости в данный момент времени вдоль линии тока. Конвективное ускорение всегда равно ну­лю в прямых каналах (или трубках тока) постоянного сече­ния при течении несжимаемой жидкости.

В проекциях на оси х, у, z уравнение (2.7) примет вид:

(2.8)

Уравнение неразрывности — это уравнение материального баланса. Зафиксируем в пространстве произвольный объем V (рис. 2.4). Масса жидкости в объеме .

Изменение массы во времени

(2.9)

м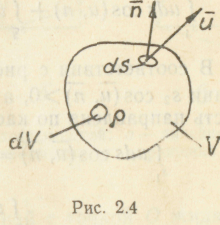 ожет произойти только за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность s объема V.

Если — внешняя нормаль к поверхности ds, то с учетом (2.5) приток

(2.10)

Приравняв выражения (2.9) и '(2.10), получим уравнение нераз­рывности в интегральной форме:

(2.11)

Слагаемое (2.10) с учетом теоремы о кратных интегралах (теоремы Остроградского-Гаусса) можно преобразовать к виду

Подставим это выражение в (2.11). Просуммируем под­ынтегральные функции. Получим

Поскольку предел интегрирования V произволен, то по­следний интеграл может быть равен нулю только при усло­вии, что

(2.12)

Уравнение (2.12)—это уравнение неразрывности в диф­ференциальной форме.

Для несжимаемой жидкости =const; и уравне­ние примет вид

(2.13)

или

(2.13’)

Для потока несжимаемой жидкости в трубке тока уравнение (2.11) принимает вид

или

В соответствии с рис. 2.2 в сечении s cos( ) <0, в се­чении s₂ cos( , )>0, а на поверхности s₆ cos( , )=0 (ско­рость направлена по касательной к s_б). Поэтому

и уравнение неразрывности для трубки тока

(2.14)

Скорость деформации. Скорость жидкости в точке, отстоящей от точки А (рис. 2.5) на расстоянии dr, можно вычислить по формуле

или

(2.15)

Различие скоростей возникает из-за:

а) растяжения жидкостного элемента (рис. 2.6, а) — линейной деформации;

б) угловой деформации (рис. 2.6, б);

в) вращения элемента без деформации (рис. 2.6, в) —

Следовательно, различие скоростей в результате деформации жидкостного элемента

(2.16)

Прежде чем приступить к расчету по известному полю скоростей u=u(x, y, z), вспомним, каков кинематический смысл частных производных.

1. Кинематический смысл ди_х/дх.

Пусть в системе координат, связанной с точкой О жидко­сти, за время dt точка А переместится и займет положение А (рис. 2.7). Тогда удлинение отрезка АА₁=(и_Ах—u )dt, и, так как для бесконечно малого отрезка ОА

, то .

Скорость удельного удлинения отрезка ОА или скорость линейной деформации вдоль оси х

(2.17)

По аналогии и – скорости линейных деформаций вдоль осей у и z

соответственно.

Уравнение неразрывности несжимаемой жидкости (2.13'), представленное в виде

говорит о неизменности объема элемента жидкости при его линейной деформации.

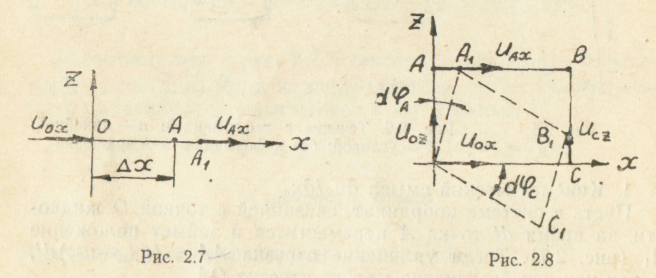
2. Кинематический смысл и_х/z и и_z/x.

Пусть за время dt точка А переместится в А₁, В—b₁, C—C₁ (рис. 2.8).

Поскольку

то

Угол поворота линии ОА , а линии ОС , т. e. частные производные du_x/dz и ди /дх равны угловым скоростям вращения линий ОА и ОС соответственно.

Суммарная угловая деформация прямоугольника ОАВС

.

Скоростью угловой деформации в плоскости х— z называется величина

Т.е.

(2.18)

По аналогии, рассмотрев угловые деформации в плоско­стях ху и уz, найдем

(2.18’)

(2.18’’)

Среднее значение угла поворота прямоугольника ОАВС

а угловая скорость

(2.19)

По аналогии нетрудно найти

(2.19’)

(2.19’’)

Вычислим du_вр, входящее в (2.16)

Подставим найденное выражение в (2.16) и запишем его в проекции на ось х:

С учетом (2.19') и (2.19"), а также (2.17), (2.18) и (2.18') после преобразований получим

По аналогии

Матрица, составленная из девяти компонентов скоростей линейных и угловых деформаций называется тензором ско­ростей деформаций S.

(2.20)

Она симметрична относительно главной диагонали, т. е. , , , и применительно к несжимаемой жидкости независимо от ориентации координатных осей