7.10. Высота всасывания центробежного насоса

По мере увеличения высоты h (рис. 7.20) установки насоса давление в жидкости перед насосом уменьшается. Предельное минимальное давление в жидкости равно давлению насыщенных паров р_н._п. При р = р_н._п происходит парообразование в жидкости, т. е. начало ее кипения. Образовавшаяся парожидкостная смесь при последующем перемещении в межлопаточном пространстве колеса насоса попадет в область повышенных давлений (р>р_и._п). Здесь происходит быстрая конденсация паров, жидкость мгновенно заполняем остающиеся полости, происходят гидравлические удары, вызывающие появление микротрещин на поверхности деталей насоса, а затем и разрушение их. Описанное явление называется кавитацией. Недопустимо эксплуатировать насос при наличии кавитации, т. е. необходимо соблюдать условие, чтобы давление в насосе р>р_н._п. В соответствии с уравнением Бернулли (7.7) давление в жидкости понижается с увеличением высоты и с ростом скорости течения жидкости. Наибольшая скорость на участке всасывания имеет место при входе жидкости на лопатки колеса (и ), при этом логично рассматривать самую верхнюю точку 1 (z₁ = h + D /2).Составим уравнение Бернулли для сечений 0 к С (см. рис. 7.20). В сечении 0: z₀=0; р₀; ₀ = 0; в сечении С: z₁=h+D p /2; . Потери на участке 0—С можно представить в виде

где — гидравлические потери во всасывающей линии, т. е. на участке 0—a; гидравлические потери внутри насоса, на участке а—С. Решив уравнение (7.1) относительно h, найдем

Обозначим

При получим максимальную высоту установки центробежного насоса

Коэффициент зависит только от конструктивных размеров насоса. Кроме того, , где Q — производительность насоса; Q_yт — утечки, т. е. расход жидкости, протекающий через неплотности внутри насоса; — площадь входного сечения жидкости в колесо, т. е. для каждого насоса (Q, геометрия насоса). Эта зависимость, находящаяся экспериментально, называется кавитационной характеристикой насоса.

7.11. Высота всасывания поршневого насоса

Если поршень насоса имеет кривошипно-шатунный привод, то скорость его с неравномерна во времени и

(7.41)

где R — длина кривошипа.

При перекачивании несжимаемой жидкости скорость во всасывающем трубопроводе переменна во времени:

(7.42)

(s — площадь поршня; s_b — площадь сечения всасывающего трубопровода), т. е. для расчета высоты установки насоса необходимо использовать уравнение Бернулли при неустановившемся течении жидкости (7.6).

Применим его для сечений 0 и 1 (рис. 7.21). В сечении О—0: z₀=0; ро, =0. В сечении 1-1: z = h+D/2; p ; =c.

(7.43)

где первое слагаемое включает потери во всасывающем трубопроводе, а второе — потери внутри насоса (главным образом гидравлические потери во всасывающем клапане).

Гидравлические потери в данном случае можно рассчитать по формуле

С учетом (7.41) и (7.42) получим

(7.44)

Как и в предыдущей задаче, h_max найдем при p =p_н._n. С учетом (7.41) — (7.44)

(7.45)

Из анализа (7.45) следует, что . Физически очевидно, что в качестве расчетной можно принять лишь минимальное из значений .

Найдем положение кривошипа, т. е. угол , отвечающее минимуму функции (7.45). Для этого с учетом того, что x=R(1—соs ) вычислим и приравняем нулю производную

(7.46)

где

Условие (7.46) выполняется (и возможен минимум) при sin₁=0 или при

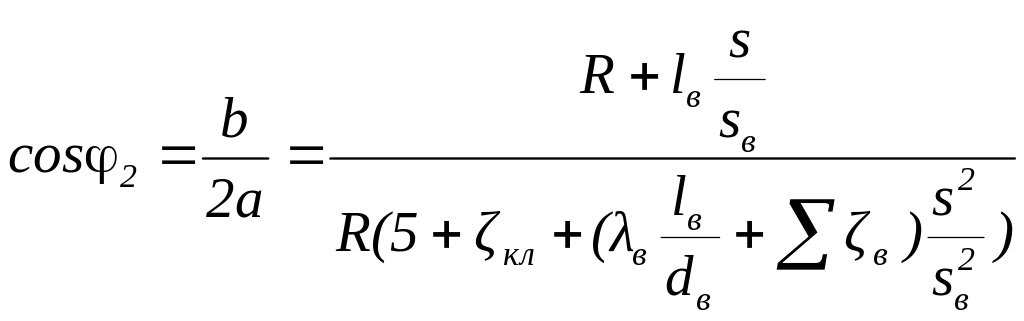
Для увеличения высоты всасывания нередко перед насосом на линии всасывания устанавливают воздушный колпак (рис. 7.22). При этом на участке всасывающего трубопровода имеет место практически установившееся течение жидкости.

Неустановившимся течение остается лишь на коротком трубопроводе между колпаком и насосом и внутри самого насоса.