Интегральные соотношения теории поля. Поток векторного поля.

П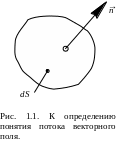 усть dS (рис. 1.1) – элемент поверхности, а – единичный вектор, направленный по внешней нормали. Потоком векторного поля (например, ) называют поверхностный интеграл вида

(1.10)

Если рассматривается векторное поле ротора ( ), то поток этого поля представляется как

(1.11)

1.4.2. Циркуляция вектора поля.

Пусть рассматривается векторное поле какой-то величины . Циркуляцией вектора вдоль контура L называют криволинейный интеграл вида

(1.12)

Иногда этот интеграл интерпретируется как «работа» векторного поля вдоль контура L. Если циркуляция векторного поля вдоль замкнутого пути (контура) равна нулю, то поле называют потенциальным.

Формула Стокса.

Эта формула позволяет преобразовать криволинейный интеграл вдоль замкнутой пространственной кривой в поверхностный интеграл по поверхности, натянутой на эту кривую, т. е.

(1.13)

т. е. циркуляция вектора поля вдоль контура равна потоку вихря через поверхность, ограниченную этим контуром.

Формула Остроградского – Гаусса.

Это соотношение, часто называемое преобразованием Остроградского – Гаусса, связывает поверхностный интеграл по замкнутой поверхности с интегралом по объему, ограниченному этой поверхностью

(1.15)

Формула показывает, что поток векторного поля через замкнутую поверхность равен интегралу от дивергенции поля по объему, ограниченному этой поверхностью.

В механике жидкости широко используется формула, являющаяся следствием формулы Остроградского – Гаусса для скалярного поля

(1.16)

где – какая-то скалярная функция.

1 Сновные понятия и определения

При проведении теоретического анализа поведения жид­костей и газов в гидромеханике пользуются понятием «сплошная среда» — материальное тело, непрерывно распределенное в пространстве. Введение этого понятия позволяет проводить дифференцирование, предопределяет плав­ное изменение параметров в любой точке пространства. Правомерность этой гипотезы доказана согласием теории и эксперимента в многочисленных задачах гидромеханики.

Плотность среды в произвольной точке пространства определяется соотношением , где Dm — масса жидкости, находящейся в объеме DV. Размерность [r] = кг/м3. Плотность среды зависит от температуры Т и давления р. Связь r = r(р, Т) называется уравнением состояния (для газов это уравнение Менделеева—Клапейрона; p/r= nRT; R — газовая постоянная).

Сжимаемость жидкости определяется производной . Несмотря на значительную сжимаемость газов по сравнению с жидкостями при скоростях в средах m<0,1с (с — скорость звука в среде), при решении конкретных задач сжимаемостью можно пренебречь. Поэтому понятие “несжимаемая жидкость” нашло широкое применение.

Вязкость жидкости характеризует способность ее сопротивляться сдвиговым усилиям.

Если между двух параллельных пластин (рис. 1.1) поместить жидкость, то для приведения верхней пластины в движение со скоростью u необходимо приложить силу F, причем

(1.1)

где S – площадь пластин; d – расстояние между ними; m – коэффициент пропорциональности, называемый коэффициентом динамической вязкости.

Размерность в системе СИ: , в системе СГС:

В условиях ламинарного течения между пластинами установится линейный профиль скоростей (см. рис. 1.1), тогда . Кроме того, f/s=t, где t — касательное напряжение. Тогда соотношению (1.1) можно придать вид

(1.2)

Уравнение (1.2) выражает закон внутреннего трения Ньютона при одномерном течении.

Наряду с коэффициентом динамической вязкости в гидродинамике используется и коэффициент кинематической вязкости:

(1.3)

Размерность в СИ: [n]=м²/c, в СГС: [n]=см²/c= 1 стокс (Ст); 1 Ст=10^-4 м²/с.

Вязкость воды при 20 °С n=1сСт=10^-2 Ст =10^-6 м²/с; m=10^-3 Па×с.

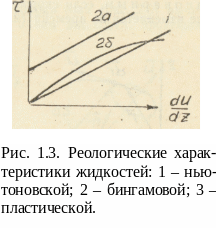
Вязкость жидкостей и газов существенно зависит от температуры, причем с ростом температуры вязкость газов возрастает, а жидкостей — падает (рис. 1.2).

Жидкости, которые при постоянной температуре характеризуются уравнением (1.2) с постоянным коэффициентом m, называются ньютоновскими (вода, керосин, спирт и др.). Реологическая характеристика их (зависимость имеет вид прямой, проходящей через начало координат (рис. 1.3).

Жидкости с характеристиками любого другого вида называются неньютоновскими (бингамовские, пластические и пр.). Дисциплина, изучающая механику неньютоновских жидкостей, называется реологией.

В теоретической гидромеханике для упрощенного решения задач введено понятие идеальной жидкости. Это сплошная среда, у которой n=m=0; r¹0.