7.8. Вторичные токи в реальной жидкости

Вторичными называются течения, возникающие в поперечном сечении каналов из-за наличия вязкости жидкости. В качестве примера рассмотрим течение жидкости в цилиндрическом

змеевике (рис. 7.14), выполненном из трубы диаметром d. В центре потока из-за наличия плавного поворота создается центробежное поле давлений и p_A>p_B (рис. 7.15). В жидкости, примыкающей к стенке, движение отсутствует, т. е. центробежное поле давлений возникнуть не может. Уcловие отсутствия движения жидкости в поперечном сечении— это равенство давлений при r=const, т. е. p_A>p_C; p_B>p_D, Это условие в реальной жидкости невыполнимо, и вблизи стенки возникает движение, направленное к оси змеевика, в ядре потока — от оси змеевика.

Вторичные токи вызывают деформацию профиля скоро стей, смещение максимума скоростей (рис. 7.15). В результате изменяются как сопротивление канала .(рис. 7.16) так и характер смены режимов (рис. 7.17).

При течении жидкости в змеевике различают:

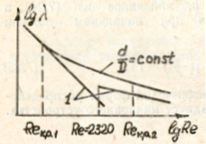
1. Ламинарный режим течения Re<Re_Kp (область 1 на рис. 7.16) —это область, где кривизна канала не влияет на его сопротивление.

2. Ламинарный режим с вторичными токами Re_KP2>Re>>Re_Kp (область 2).

3. Турбулентный режим (область 5) Re> Re_Kp , в этой области линии =f(Re) для змеевика и прямого каналов параллельны. Для расчета сопротивления змеевика при турбулентном режиме течения жидкости можно воспользоваться эмпирической зависимостью 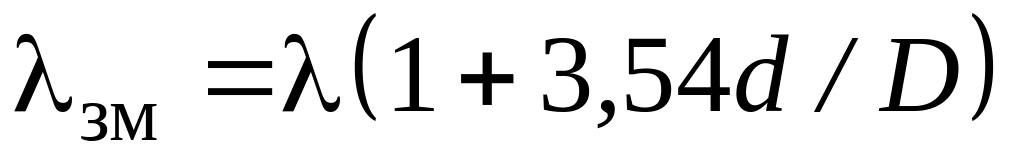, где  — коэффициент гидравлического трения прямой трубы.

7.9. Гидравлический удар в трубах

Если внезапно остановить движущийся в трубе поток жидкости, то в соответствии с уравнением (3.1) изменение количества движения вызовет возникновение избыточной силы давления жидкости на задвижку (рис. 7.18). Очевидно, что абсолютно несжимаемая жидкость вызвала бы бесконечное по величине давление при мгновенной остановке в недеформируемом трубопроводе. Однако в результате сжимаемости реальных жидкостей остановка жидкости в трубе даже при мгновенном закрытии заслонки происходит во времени, и волна давления распространяется в среде со скоростью, равной скорости звука с. Таким образом, остановка жидкости на участке длиной х произойдет за время t=x/c, при этом количество движения изменится линейно от начального до 0, т.е.

(7.26)

где — средняя скорость течения жидкости в трубе до остановки; s — площадь сечения трубопровода.

В результате изменения количества движения возникнет

(7.27)

Приравняв (7.26) и (7.27), получим выражение для расчета скачка давления р, возникающего при гидравлическом ударе:

(7.28)

После остановки жидкости во всем объеме трубы начинается процесс послойного расширения. Слева направо идет волна разрежения. Итак, перед заслонкой давление р₀ сохраняется в течение времени Т=2l/с. Величина Т называется фазой прямого удара. Более детальный анализ гидравлического удара проведем на основании уравнения движения (5.1) и уравнения неразрывности (2.12) идеальной сжимаемой жидкости. Анализ проведем в предположении, что в уравнении динамики можно не учитывать сжимаемость, т. е. считаем относительное изменение плотности жидкости незначительным. В этом случае при течении вдоль оси х в каналах постоянного сечения конвективное ускорение равно 0, т. е.

уравнение (5.1) в проекции на ось х примет с учетом того, что X=0, вид

(7.29)

(дополнительно принять, что u_x= ).

Уравнение (2.12) для одномерной задачи можно записать так

(7.30)

Если плотность жидкости однозначно определяется давлением (такие жидкости называются баротропными), т. е. = (р), то в (7.30) Производная d /dp всегда больше нуля и постоянна. Обозначим dp/d =c². С учетом этого уравнение (7.30) примет вид

(7.31)

(для газов p/ =nRT; при T=const dp/d =RTn=const).

Решим совместно уравнения (7.29) и (7.31). Продифференцировав (7.29) по t, (7.31) по х и приравняв смешанные вторые производные, найдем

(7.32)

По аналогии, взяв соответственно производные по х и t, получим

(7.33)

Уравнения (7.32) и (7.33) называются в математике волновыми. Они могут быть проинтегрированы в общем виде введением новых переменных

и (7.34)

Решения имеют вид

(7.35)

(7.36)

В случае закрытия трубопровода в начальный период имеет место одна волна и решение (7.35) и (7.36) с учетом (7.34) следует искать в виде

(7.37)

Из (7.37) видно, что р—p =const, если t- =const, т. е. если х с течением времени изменяется со скоростью с. Таким образом, с — это скорость распространения ударной волны (скорость звука). Решение (7.37) показывает, что распределение давлений, сформированное по х в момент времени t, отвечающее функции f(0- ), остается по форме неизменным во времени, но целиком смещается вдоль оси х со скоростью с. Подставив (7.37) и (7.38) в выражения (7.29) и (7.31), нетрудно показать, что

Тогда (7.38) примет вид

(7.39)

Приравняв (7.37) и (7.39), получим p—p₀ = c( ), а при полной остановке жидкости ( =0) —уравнение (7.28). Во входном сечении, т. е. при х=1, давление во времени не может измениться и р=p =const. Здесь зарождается отраженная волна . Из (7.35) следует, что для этого сечения =0 или

(7.40)

т. е. обратная волна является отражением прямой с переменой знака.

При мгновенном закрытии задвижки (при = 0) из (7.39) имеем f=—pc , следовательно, =pc . При своем движении вправо волна , складываясь с f, дает р—р₀ = 0. Волна достигнет нулевого сечения за время Т=2l/с, здесь она отражается от заслонки без изменения знака и начинается распространение влево волны разрежения.

Если время закрытия задвижки t₃<T, то максимальное давление определится уравнением (7.28), а удар называется прямым гидравлическим ударом. Если t₃>T, то возникающий при этом гидравлический удар называется непрямым. Максимальный перепад давлений, возникающий при таком ударе, можно найти на основе анализа, аналогичного приведенному выше, и рассчитать по приближенной формуле

где

Выполненный анализ показывает, что давление прямого гидравлического удара не зависит от длины трубопровода и значительно по величине. Так, при течении воды ( = 10 кг/м³; с= 1435 м/с) со скоростью =1 м/с р—р₀ =1,43510⁶ Па 14 ат.

Возможны следующие способы уменьшения ударного давления:

1. Установка запорной арматуры, не допускающей быстрого закрытия трубопровода.

2. Уменьшение инерционных сил путем установки воздушного колпака (рис. 7.19). Здесь время остановки жидкости увеличено за счет сжимаемости газа.