7.6. Истечение жидкости

При истечении жидкости через отверстие или насадки из сосуда под давлением р₀ для расчета скоростей и расходов используются зависимости

(7.19)

(7.20)

где — некоторая теоретическая скорость, достигаемая при отсутствии гидравлических потерь в жидкости;

 – коэффициент скорости;

 – коэффициент расхода;

S₀ — площадь сечения отверстия или насадка.

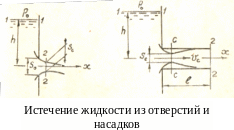
Рассмотрим различные случаи истечения:

а) истечение жидкости через отверстие с острой кромкой. При выходе жидкости из отверстия (рис. 7.8) наблюдается сжатие струи с коэффициентом сжатия . Составим уравнение Бернулли (7.7) для сечений 1 и 2, где 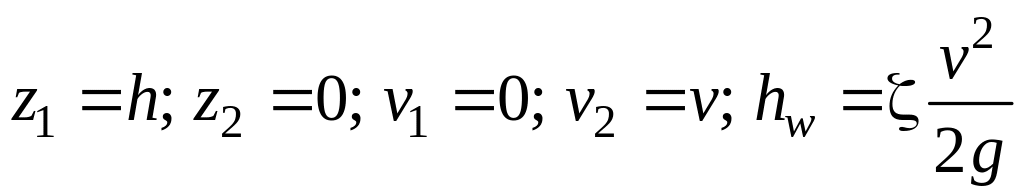. Решим (7.1) относительно и сопоставим с .(7.19). Найдем, что при

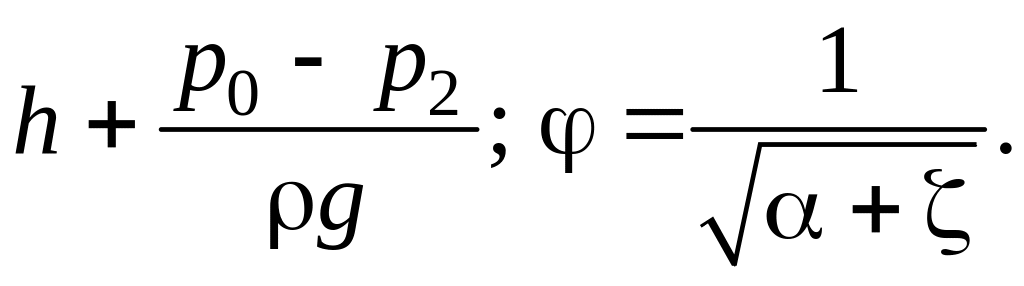(7.21)

Поскольку , то с учетом (7.20)  = . Экспериментально найдено, что при турбулентном режиме истечения =0,62 0,64; =0,60 0,62; при ламинарном  и  существенно зависят от Re;

б) истечение жидкости через цилиндрический насадок. При входе жидкости в патрубок в сечении C – C (рис. 7.9) происходит сжатие струи до величины S_с. Далее следует расширение потока до величины S₀.

В уравнении Бернулли, записанном для сечений 1 и 2, z₁=h; z₂=0; v₁ = 0; p₁ = p₀; p₂ = p₀; h_w=h_c+h_в.р+h_l, где гидравлические потери при сжатии потока ; при расширении потока с учетом (7.18)

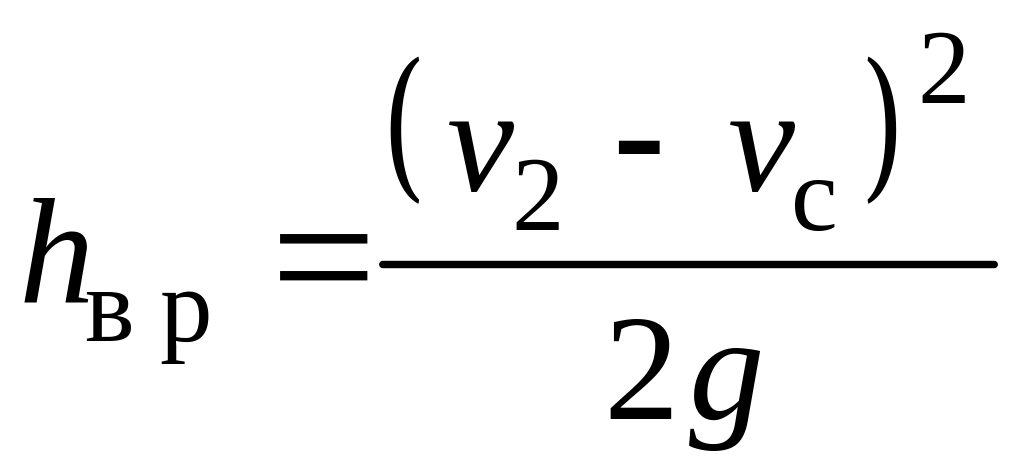
Для коротких насадков гидравлическими потерями по длине можно пренебречь. С учетом выше отмеченного и соотношений , нетрудно найти выражения для расчета v₂ и Q, сопоставив некоторые с (7.19) и (7.20), получим

Экспериментально найдено, что при турбулентном истечении =0,80 0,82. Длина патрубков l принимается обычно равной 3—4 диаметра. Это обеспечивает завершение расширения потока внутри насадка. Если составить уравнение Бернулли для сечений с и 2, то при =1 найдем

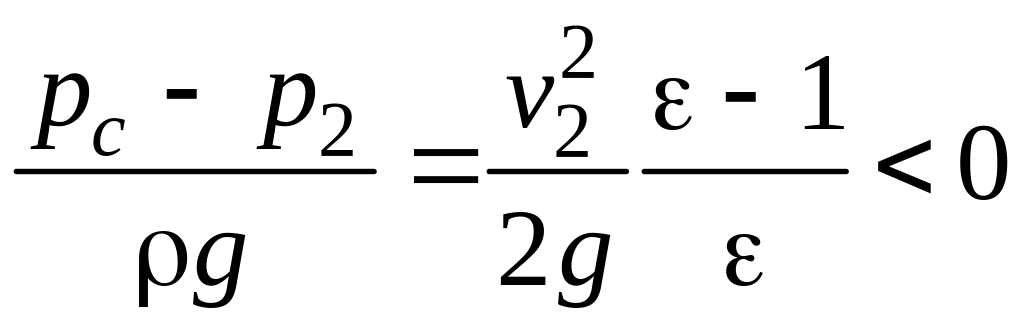
т. е. р_с<р₂.

Картина истечения между сечениями 1 и с аналогична картине истечения через отверстие (см. рис. 7.8), но в насадке жидкость истекает в область пониженного давления. Этим объясняется увеличение расхода Q по сравнению с отверстием;

в) истечение жидкости через водослив прямоугольного сечения (рис. 7.10) шириной В. Расход в слое dz с учетом (7.20) составит . Проинтегрируем это выражение по z от 0 до Н, получим после преобразований , где m 2/3—коэффициент расхода водослива; m=0,45;

г) опорожнение вертикального цилиндрического сосуда

(рис. 7.11). При S₀<<S можно считать течение установившимся.

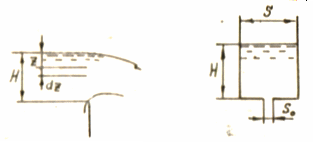
Пусть в момент времени t уровень жидкости равен H. Тогда за dt с учетом (7.20) вытечет объем

и уровень жидкости понизится

Разделив переменные, проинтегрируем это уравнение при начальном условии Н=Н₀ при t=0. Получим, что время опорожнения сосуда t=2V₀/Q₀, где V₀=SH₀; Q₀=S₀ ; V₀, Н₀ — начальные объем и уровень жидкости в сосуде.

7.7. Поле скоростей и давлений в циклонном устройстве

В отличие от ранее рассмотренного относительного покоя (см. рис. 4.7), где вращение внутренним слоям жидкости передавалось за счет сил трения, в циклоне движение центральных слоев происходит за счет перемещения вращательно движущейся жидкости от периферии к центру (рис. 7.12).

Приведем решение задачи при течении идеальной жидкости. При движении жидкости в плоскости ху координата z=const и полный дифференциал уравнения Бернулли (5.8) можно записать в виде

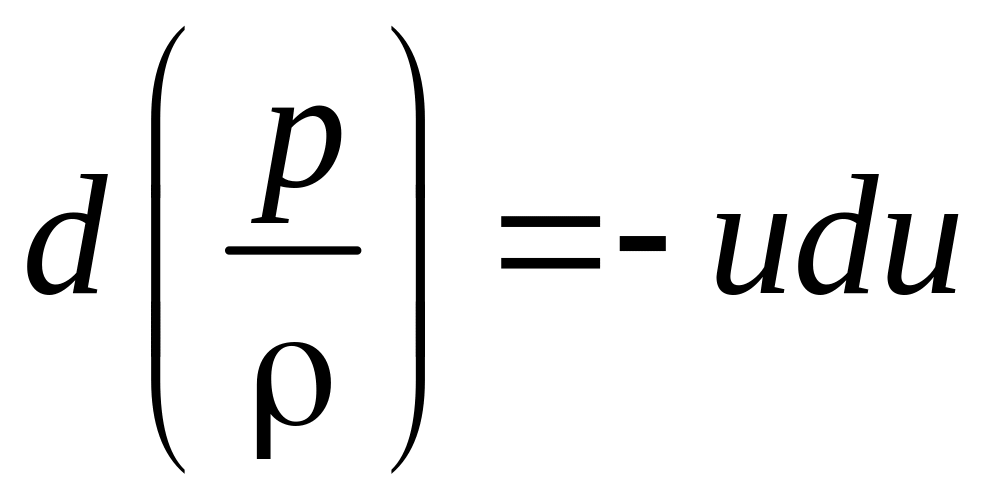(7.22)

Поскольку радиальная составляющая скорости u_R<<u, то в уравнении движения (5.1) при проектировании его на радиальное

направление можно пренебречь слагаемым .С учетом того, что , a получим 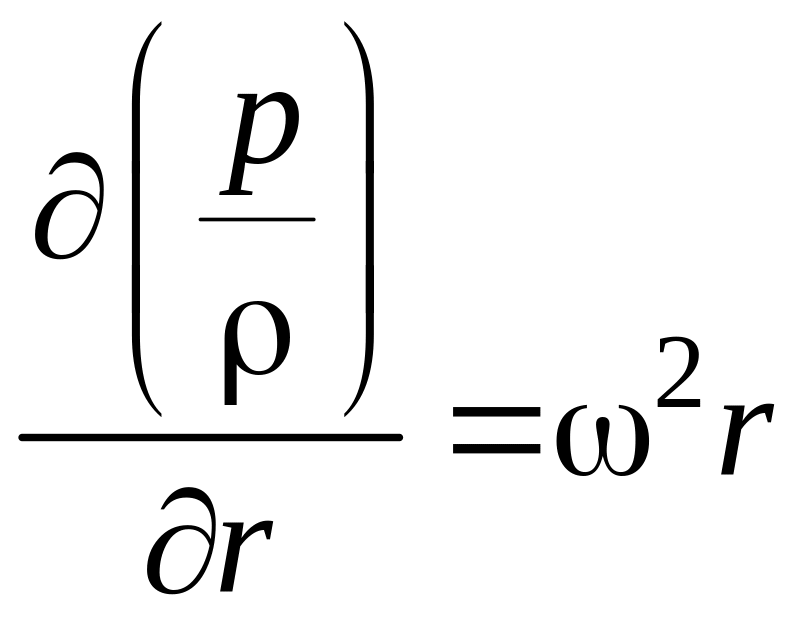, или, так как в условиях данной задачи давление зависит только от одной переменной, от r, то можно перейти к полным дифференциалам и записать

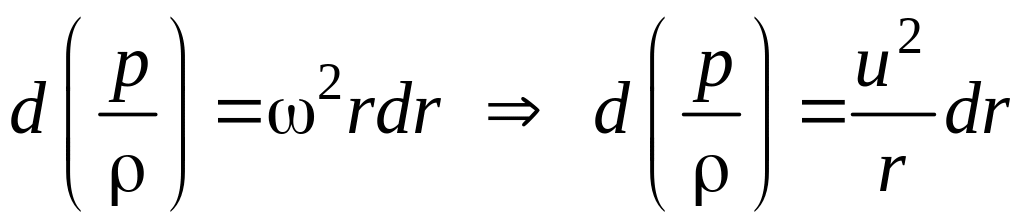(7.23)

Приравняем (7.22) и (7.23), проинтегрируем полученное при этом дифференциальное уравнение ln r= – ln u+C . При начальном условии u=u₀ при r=r₀ получим

(7.24)

Подставим выражение для и, найденное из (7.24), в (7.23). После интегрирования при начальном условии р=ро при r=r₀ найдем

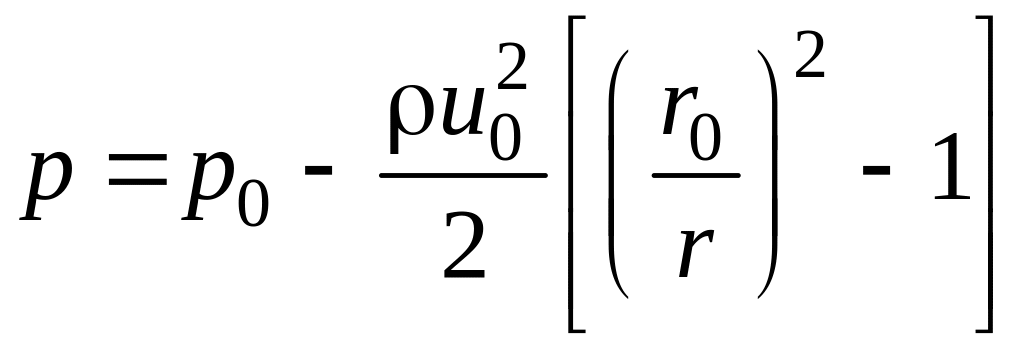(7.25)

На рис. 7.13 приведены в графической форме распределения скоростей и давлений по радиусу циклонного устройства.