7.2. Уравнение Бернулли для сети с насосом

Если выполняется условие

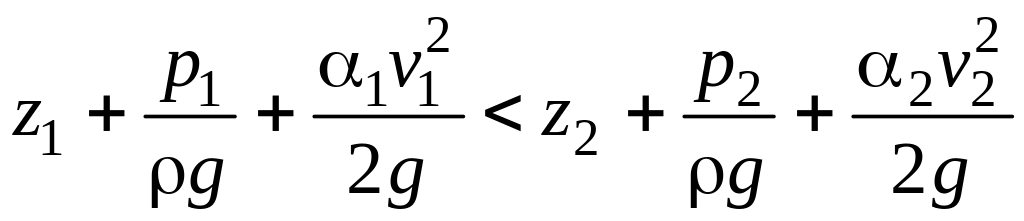
то для обеспечения подачи жидкости от сечения 1 к 2 необходимо сообщить ей энергию внешним источником, или насосом.

Удельная энергия, сообщаемая жидкости насосом, называется полезным напором и обозначается Н, м. Уравнение баланса энергий в этом случае имеет вид

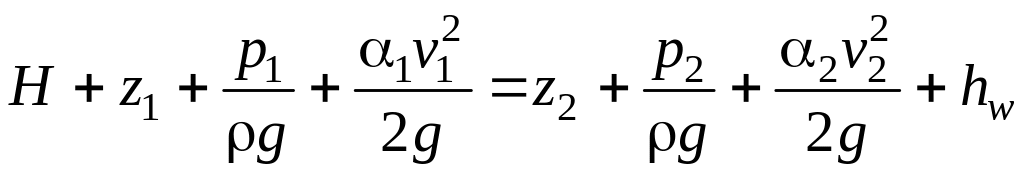(7.8)

Это уравнение позволяет для заданной схемы трубопроводов рассчитывать Н, а следовательно, подобрать насос. Поскольку слагаемые 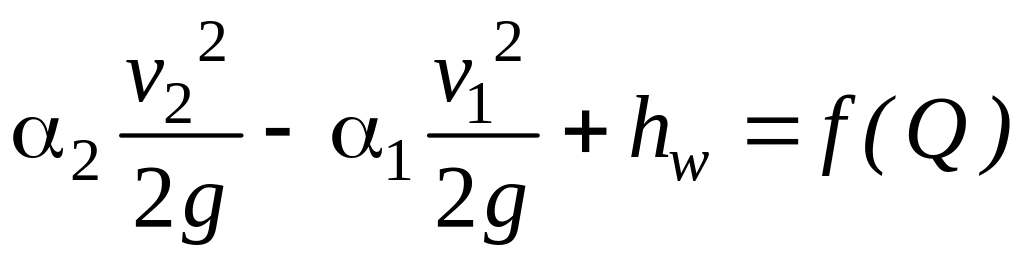, то уравне ние (7.8) можно записать так:

(7.9)

Эта зависимость называется характеристикой сети

7.3. Гидравлические потери по длине

Составим уравнение Бернулли (7.7) для горизонтального участка трубы (см. рис. 6.8). В этом случае . Из (7.7) получим или с учетом (6.12)

(7.10)

Уравнение (7.10) можно получить из (7.2) с учетом (3.19) и (6.26).

7.4. Гидравлические потери на местных сопротивлениях

Для расчета их используется формула

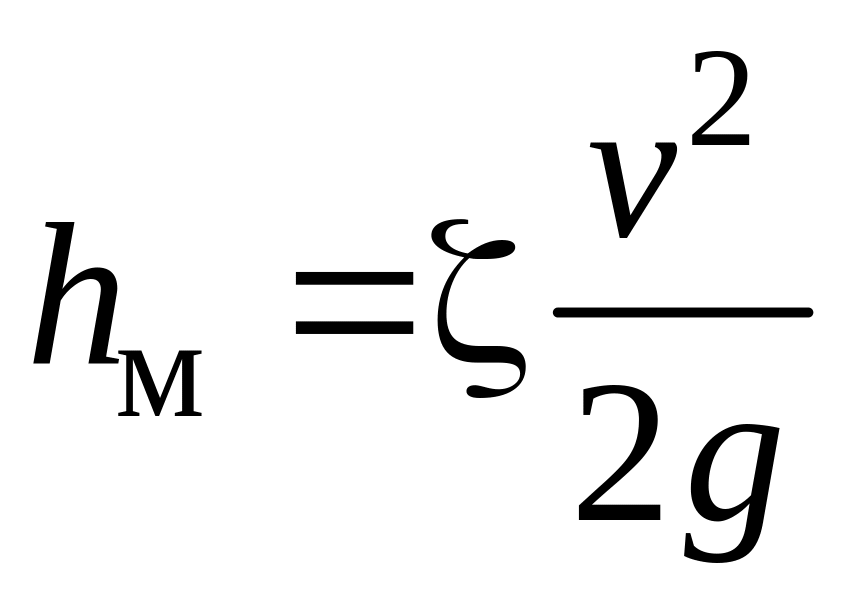(7.11)

где  — коэффициент местного сопротивления, обычно определяемый опытным путем.

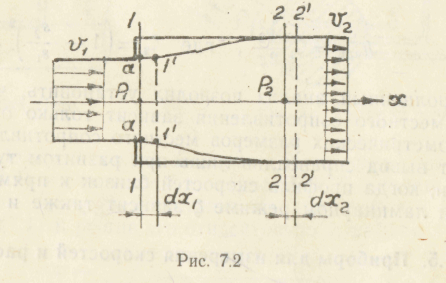
Гидравлические потери при внезапном расширении (рис. 7.2) можно найти аналитически. Рассмотрим решение этой задачи подробно (в гидравлике она получила название «Теорема Борда»).

К жидкости, находящейся в момент t в объеме между сечений 1—1 и 2—2, применим теорему об изменении количества движения (3.2). В проекции на ось х

(7.12)

где

(7.13)

За время dt жидкость сместится (сечение 1-1 в 1—а—1'—1'—а—1, сечение 2—2 в 2'—2') и займет объем . Изменение количества движения составит

(7.14)

Предположив, что в выбранных сечениях эпюра скоростей прямоугольная, и получим

. С учетом того, что , уравнение (7.14) можно привести к виду

(7.15)

Подставим (7.15) и (7.13) в (7.12), найдем

(7.16)

Для нахождения гидравлических потерь применим уравнение Бернулли (7.7) для сечений 1 и 2. Поскольку , то

(7.17)

В условиях, когда в сечении u= ; =1 с учетом (7.16), получим уравнение Борда для расчета гидравлических потерь при внезапном расширении потока:

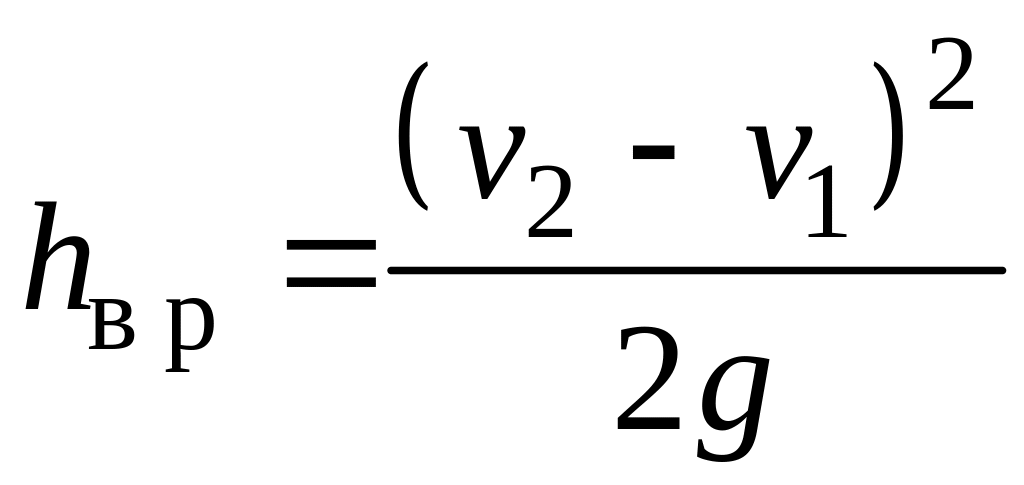(7.18)

С учетом соотношения представим (7.18) в виде (7.11):

, где

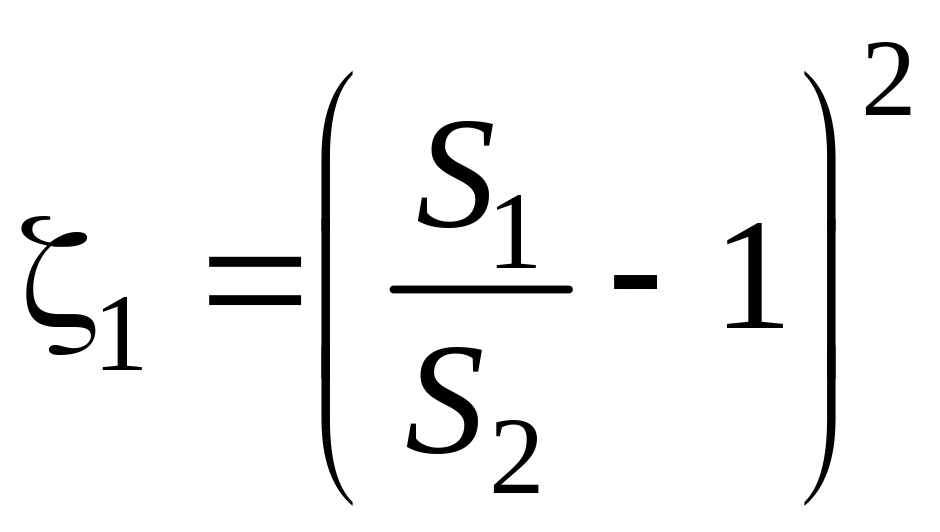
или

, где

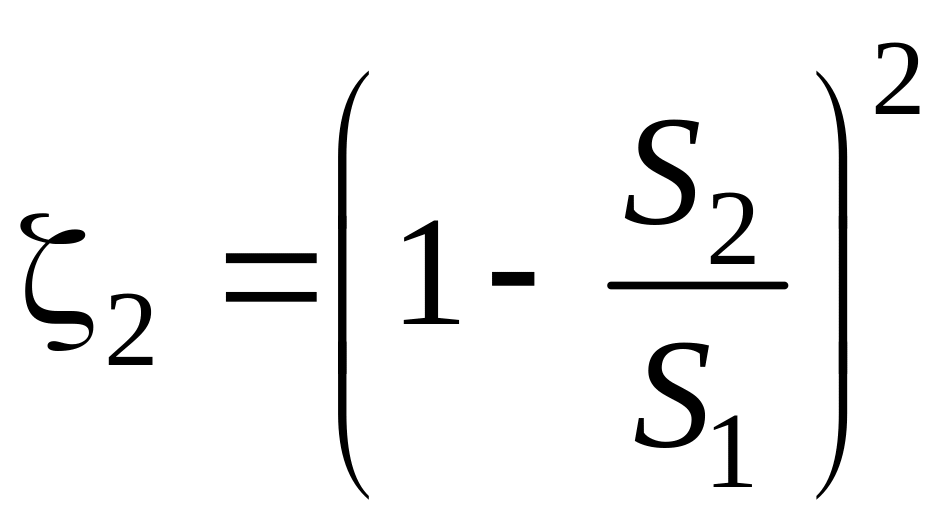
Выполненный анализ позволил установить, что коэффициент местного сопротивления зависит только от соотношения геометрических размеров местного сопротивления. Однако этот вывод справедлив лишь при развитом турбулентном течении, когда профиль скоростей близок к прямоугольному.

При ламинарном режиме зависит также и от Re.

7.5. Приборы для измерения скоростей и расходов

Здесь мы рассмотрим только те приборы, принцип действия которых может быть объяснен с помощью уравнения Бернулли:

а) трубка Пито (рис. 7.3). В пьезометрической трубке 1, или трубке статического напора, уровень жидкости . При обтекании устья трубки полного напора 2 происходит торможение потока, т. е. преобразование кинетической энергии в энергию давления, и h₂=p( g)+u²/(2g). Перепад уровней т. е. прибор позволяет измерить локальную скорость в канале:

б) плоский зонд (рис. 7.4) применяется для измерения величины и направления локальной скорости в плоском потоке. Измерив перепады уровней h₂—h и h₂—h , каждый из которых зависит от значения скорости u и угла  набегания потока, получаем возможность нахождения и и ;

в) шаровой зонд — это шарик, в теле которого выполнено пять каналов: три — как показано на рис. 7.4, у плоского зонда и еще два - смещенных относительно канала 2 в горизонтальной плоскости. Применяется для измерения направления и величины локальной скорости в пространственном потоке;

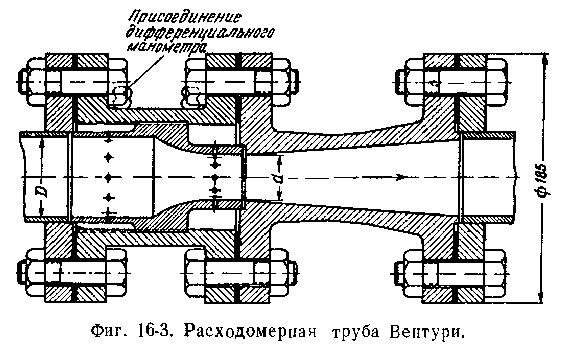
г) расходомер с соплом Вентури. Применим уравнение Бернулли (7.7) к сечениям 7 и 2 (рис. 7.5). В данном случае , . Подставив эти выражения и уравнение (2.6) в (7.1) и решив его относительно , найдем

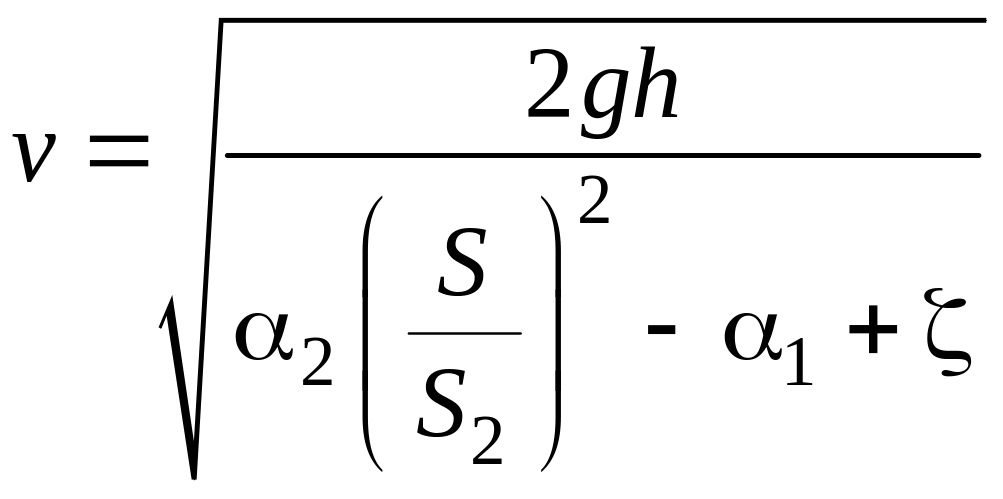
где s и s₂ – площади сечений трубы и горловины расходомера Вентури.

Расход жидкости вычислим по формуле Q= s;

д) расходомер с диафрагмой (рис. 7.6). Установка тонкостенной шайбы вызывает сжатие потока, причем в сечении 2 площадь сечения струи s_c<s₀ (s₀ — площадь сечения отверстия). Их отношение s_c/s₀= называется коэффициентом сжатия струи. По аналогии с предыдущей задачей найдем

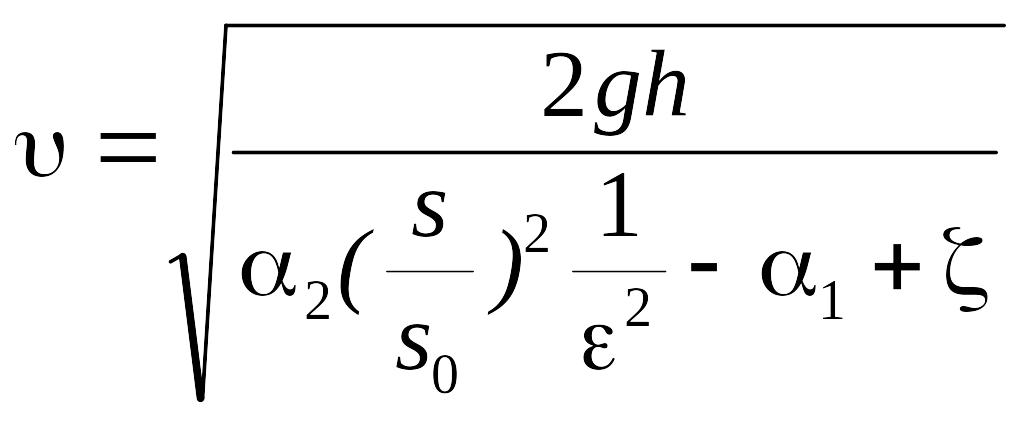
е) ротаметр (рис. 7.7) — это расходомер, выполненный из стеклянной конической трубки, внутри которой находится поплавок. При расходе жидкости Q поплавок устанавливается по высоте а. Установим вид зависимости Q=f(a). Запишем условие равновесия вертикальных

составляющих сил, действующих на поплавок:

где Vn — объем поплавка; — плотность материала поплавка; s_n —• площадь сечения поплавка.

Поскольку величины двух первых слагаемых не зависят от расхода, то для прибора р —p₂ = const. Следовательно, гидравлические потери, возникающие при обтекании поплавка,

и скорость жидкости в кольцевом канале ;

= =const. Если выполнено условие s=s₀+ka(k — коэффициент пропорциональности), то получим Q= ( s₀