6.16. Турбулентный пограничный слой на полубесконечной пластине

Так же, как и при течении в трубах, ламинарный пограничный слой при достижении критической толщины теряет устойчивость, т. е. при > пограничный слой становится турбулентным, причем 3*10⁵. Интегральное соотношение (6.56) оказывается верным и для турбулентного пограничного слоя (оно может быть получено на основе уравнения Рейнольдса (6.3)).

Решим задачу для полубесконечной пластины. При расчетах примем, что в пограничном слое справедлив универсальный профиль скоростей (уравнения (6.30) и (6.38)). Для упрощения уравнение (6.38) проаппроксимируем (см. рис. 6.7):

6.64

и, так как u_x=U при y= , то

6.65

По (6.54) с учетом (6.65) найдем

6.66

Подставив (6.33) в (6.64), можно получить

6.67

Проинтегрируем (6.57), предварительно подставив в него (6.66) и (6.67). При начальном условии =0 при x=0 получим

6.68

Из (6.62) с учетом (6.67) и (6.68) найдем

6.69

Далее можно вычислить силу трения, действующую на пластину.

6.17. Струйное течение

Применение уравнений пограничного слоя необязательно связано с наличием взаимодействия жидкости с твердыми стенками. Они могут быть применены в случае, когда внутри потока имеется слой жидкости, в котором преобладающую роль играют силы трения. Примером такого течения является ламинарное течение затопленной струи (рис. 6.13). Уравнения пограничного слоя, записанные в цилиндрических координатах с учетом того, что давление во всем объеме жидкости постоянно, примут вид:

,

,

а граничные условия

при r=0,

при r

Теоретически найденное поле осевых скоростей [1] описывается уравнением

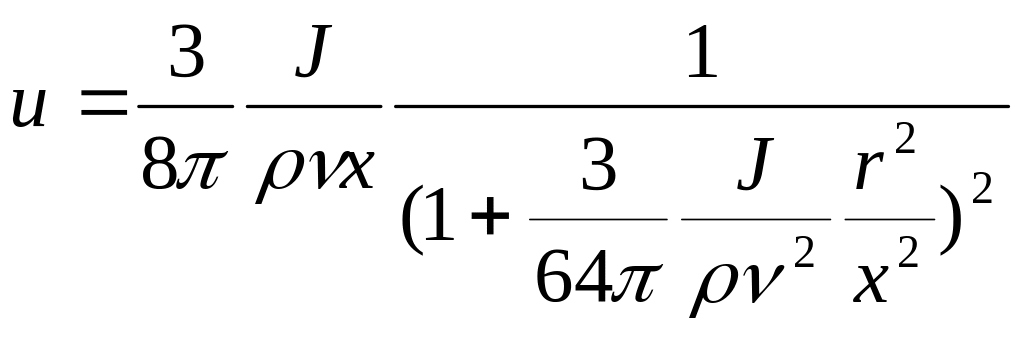(6.70)

Где — поток импульса, который постоянен в направлении оси х и равен начальному , s₀ — площадь поперечного сечения отверстия; и₀ — скорость жидкости в отверстии.

Из анализа (6.70) видно, что с удалением от отверстия скорость в струе уменьшается. При этом, однако, количество увлекаемой в движение жидкости увеличивается, струя расширяется и расход жидкости

прямо пропорционален х.

7. Одномерные течения вязкой жидкости

В прикладной гидромеханике одномерными обычно называют потоки, в которых гидродинамические величины (скорость, давление) зависят только от одной геометрической координаты. Если реальные потоки жидкости в каналах различной формы характеризовать средней расходной скоростью и давлением на оси потока, го такой поток можно считать одномерным.

7.1. Уравнение Бернулли для потока вязкой жидкости

Применим уравнение энергии в интегральной форме (3.12) — (3.16) к объему движущейся жидкости, ограниченному стенками канала s_ct и двумя живыми сечениями s_n и s_n2, причем оба сечения в тех местах, где площади сечений локально максимальны или минимальны, т. е. живые сечения плоские, а движение жидкости в них равномерно (рис. 7.1). Преобразуем последовательно все слагаемые:

Поскольку s = , и на стенке = 0, то после простых преобразований найдем:

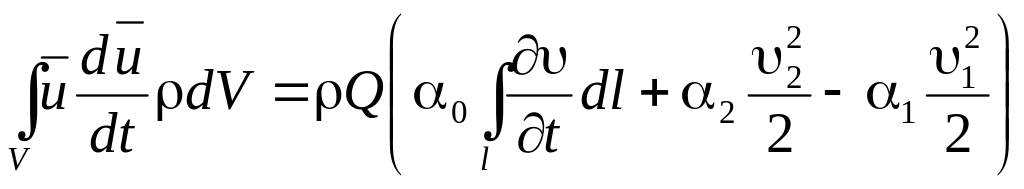(7.1)

где

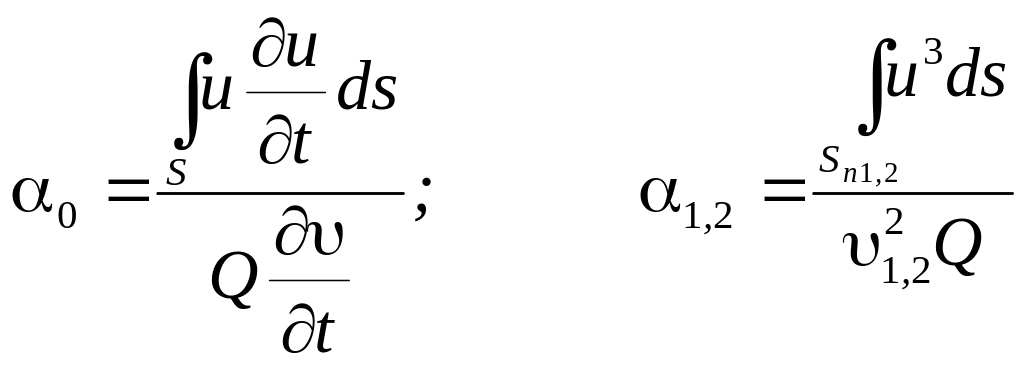
Обозначим

(7.2)

Поскольку выбранные сечения плоские, то напряжение в них р_п = -р и

(7.3)

Если течение происходит в поле сил тяжести, то , и можно показать, что

(7.4)

Просуммируем выражения (7.3) и (7.4). С учетом того, что в живом плоском сечении давление изменяется по закону статики, то p+ gz=const и

(7.5)

После подстановки (7.1), (7.2) и (7.5) в (3.12) и простейших преобразований получим

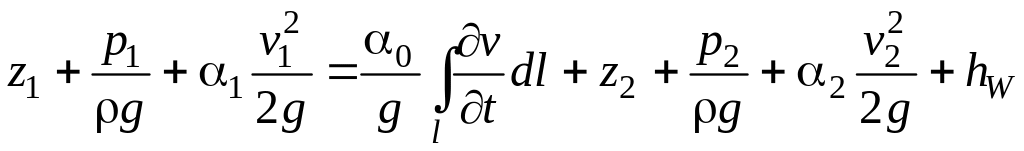(7.6)

Уравнение (7.6) представляет собой баланс энергий. Слагаемое h_w — удельная диссипированная энергия или гидравлические потери.

Гидравлические потери условно разделяются на два вида.

1. Гидравлические потери по длине 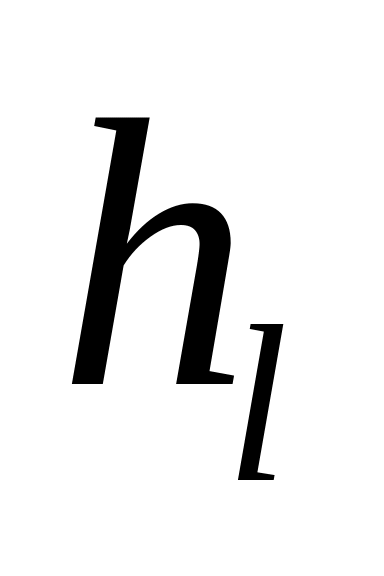. Эти потери возникают в каналах постоянного сечения и пропорциональны длине канала.

2. Гидравлические потери на местных сопротивлениях, . Эти потери возникают в местах изменения сечения канала или искривления его оси. Примеры местных сопротивлений: вентиль, кран, расширение, сужение, поворот канала и пр.

При известных эпюрах скоростей в сечении канала всегда можно вычислить коэффициенты .Так при ламинарном течении в круглых трубах с учетом (6.26) найдем , а при турбулентном, когда эпюра скоростей приближается к прямоугольной, можно принять .

В случае установившегося движения жидкости, когда и уравнение Бернулли принимает вид:

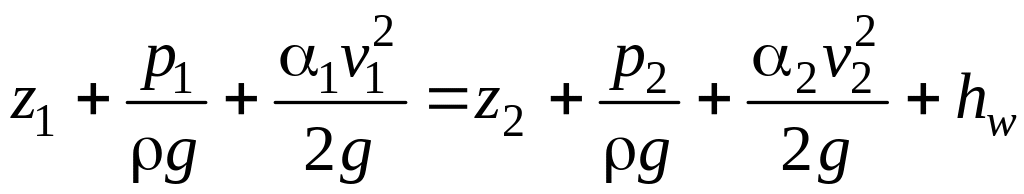(7.7)