6.9. Турбулентное безнапорное течение Куэтта

Наличие пульсационного перемешивания жидкости приводит к выравниванию скоростей в средней части потока. Профиль скоростей в канале приведен на рис. 6.6. Для нахождения аналитических выражений для профиля скоростей делаются упрощающие задачу допущения. Поток представляется в виде:

ламинарного пристенного слоя толщиной , в котором предполагается отсутствие турбулентности, и

турбулентного ядра, в котором вязкость жидкости =0. Если >, то каналы называются гидравлически гладкими, если <, то каналы – гидравлически шероховатые, где  – высота микронеровностей на поверхности канала.

При установившемся течении Куэтта в (6.3)

Х = 0; , так как течение равномерное и параметры течения вдоль оси х не могут изменяться, а , так как рассматриваемое течение плоское и =0. С учетом (3.9) и равенства уравнение (6.3) можно записать в виде

(6.29)

Поскольку при z = 0 =₀ (₀ — касательное напряжение на стенках канала), а (турбулентность отсутствует), то в (6.29) C₁ = ₀.

Найдем аналитические выражения для профиля скоростей:

а) профиль скоростей в ламинарном слое. Поскольку в нем отсутствует турбулентность, т. е. , то уравнение (6.29) упрощается: .

Проинтегрировав его при граничном условии: при z=0, , получим распределение скоростей в пристенном слое или с учетом (6.33):

(6.30)

б) профиль скоростей в турбулентном ядре потока. Приняв в (6.29)  = 0, т. е. предположив, что вязкостные напряжения в потоке малы по сравнению с турбулентными , получим

Хотя уравнение Рейнольдса в условиях данной задачи существенно упростилось, но для решения его необходимо иметь одну дополнительную зависимость, связывающую турбулентное напряжение _турб с уже имеющимися параметрами течения.

Рассмотрим модель Прандтля, устанавливающую такую связь.

Вводится понятие турбулентная вязкость _т и зависимость

. (6.31)

По аналогии с вязкостью газа принято

(6.32)

где l – длина пути перемешивания, т. е. пути, при прохождении которого жидкостная частица теряет индивидуальность, смешивается с остальным потоком; u_ – среднее значение пульсационной скорости, обычно называется динамической скоростью; . Поскольку в ядре потока , то

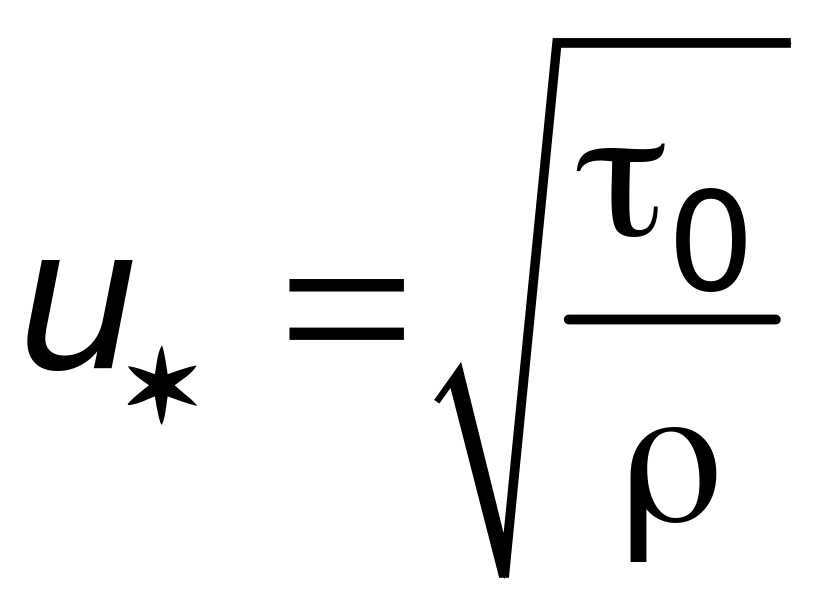(6.33)

Прандтль принял

(6.34)

где æ — коэффициент пропорциональности, æ < 1. Подставив выражения (6.32) —(6.34) в (6.31), с учетом равенства _т = ₀ последнее примет вид

После интегрирования получим

(6.35)

Э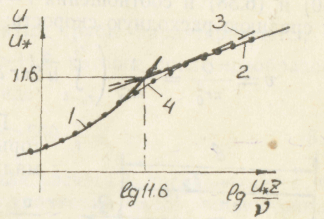 кспериментально найдено: æ = 0,4.

Рис. 6.7. Универсальный профиль скоростей Линии построены: 1 — по (6.30); 2 — по (6.38); 3— по (6.64)

Постоянную С найдем из условия равенства скоростей на границе ламинарного слоя и ядра потока, т. е. приравняв (6.30) и (6.35) при z = :

(6.36)

Подставим (6.36) в (6.35):

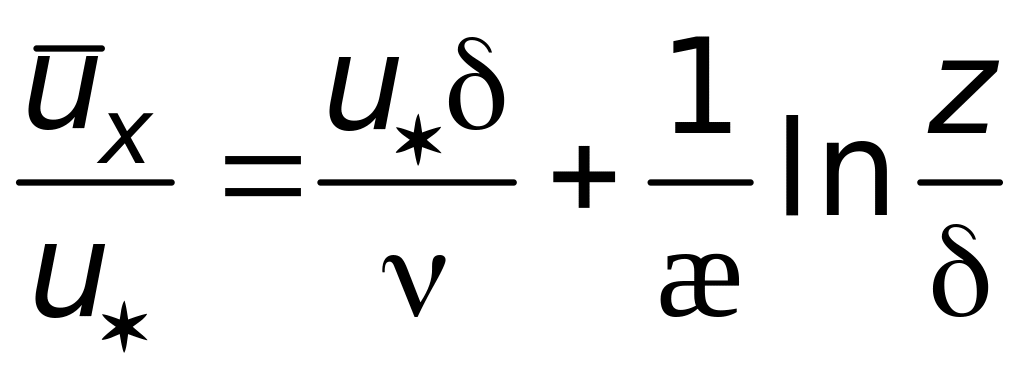(6.37)

Точные измерения профиля осредненных скоростей в потоке позволили найти æ = 0,4; u_/ = 11,6. С учетом этого (6.37) можно привести к виду

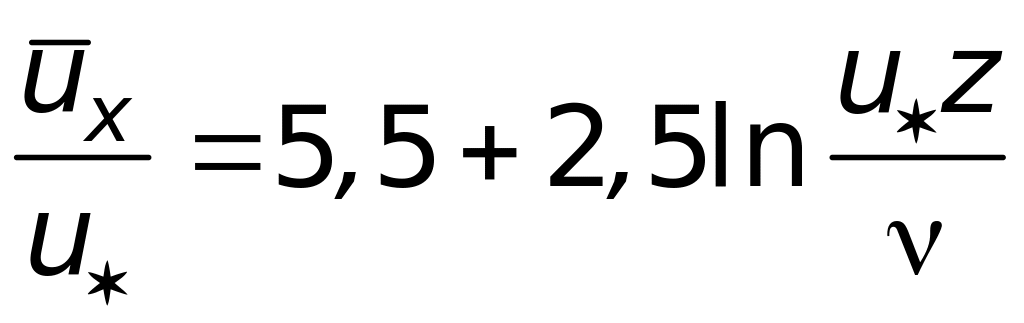(6.38)

Профиль скоростей, описываемый уравнениями (6.30) и (6.38), называется универсальным (рис. 6.7). Поскольку скорость в турбулентном потоке существенно возрастает лишь вблизи стенки, то уравнения (6.30) и (6.38) остаются приближенно верными и при отсутствии равенства _xz = const.