6.6. Равномерное ламинарное течение в плоском канале

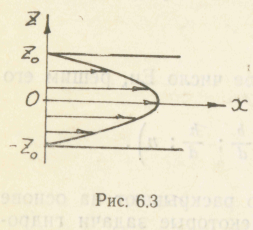
При установившемся течении жидкости вдоль оси (рис. 6.3) в горизонтальном канале u_y = u_z=0 ;X=0;du_x/dt=0.

Уравнение движения (3.21') в проекции на ось х примет вид

(6.9)

На ось z т.е. в живом сечении р =С(х)—pgz, и др/дх не зависит от z. Проинтегри­руем(6.9) дважды по z. С учетом

(1.3) и граничных условий: при z ; при z=z₀ и_х=0 получим уравнение для рас­чета распределения скоростей

Максимальная скорость (при z=0): u _m =

Вычислим расход жидкости в канале при ширине его В:

Средняя расходная скорость ,

Откуда

(6.10)

Перепад давлений в канале длиной l найдем, проинтегри­ровав (6.10) по х:

(6.11)

где р₁ и p₂ — давление в начале и конце канала соответ­ственно. Уравнение (6.11)—искомая расчетная зависимость. При решении практических задач для вычисления потерь давления при течении жидкости в горизонтальных каналах часто применяется уравнение Дарси—Вейсбаха:

(6.12)

С учетом того, что для плоского канала d₃ = 4z₀, прирав­няв (6.11) и (6.12), легко найти выражение для расчета ко­эффициента гидравлического трения X = 96/Re, справедливого для ламинарного течения.

6.7. Ламинарное течение в плоском клиновидном зазоре

Решение этой задачи иллюстрирует возникновение под­держивающей силы в подшипниках скольжения при наличии

с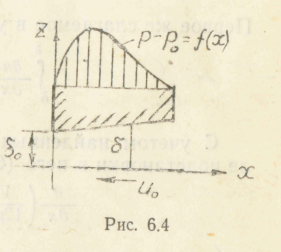 мазывающего слоя жидкости.

Пусть нижняя пластина (рис. 6.4) движется со скоростью и₀ в направлении отрицательной оси х, а давление слева и справа от неподвижной пластины равно р₀. При малой величине зазора ₀ и высокой вязкости жидкости (т. е. при Re = ) в уравнении (3.10`) можно (см. 6.4) пренебречь инерционными членами и принять = 0. Кроме того, так как и Х = 0, то уравнение движения (3.10') в проекции на ось х можно записать в виде (6.9). В тонком слое величина не зависит от z. Проинтегрируем дважды уравнение (6.9) по z:

При граничных условиях и_х=—и₀ при z=0; и_х=0 при z= ,

(6.13)

k= —параметр клиновидного слоя ( —зазор при x=l),

получим

(6.14)

Проинтегрируем уравнение неразрывности (при и_у=0) (2.13') по z.

Получим

, (6.15)

Поскольку при z=0 и при z= , то

Первое же слагаемое в условиях данной задачи

С учетом найденных соотношений уравнение (6.15) после подстановки в него (6.14) и интегрирования даст

,

т. е. выражение в скобках есть некоторая постоянная С'/2.

Тогда

(6.16)

Поскольку , то с учетом (6.13)

и уравнение (6.16) примет вид

(6.17)

Проинтегрируем (6.17) по : р=- .

Постоянные интегрирования и С" найдем из граничных условий: р = ро при х=0 и при х=1. После преобразований окончательно получим

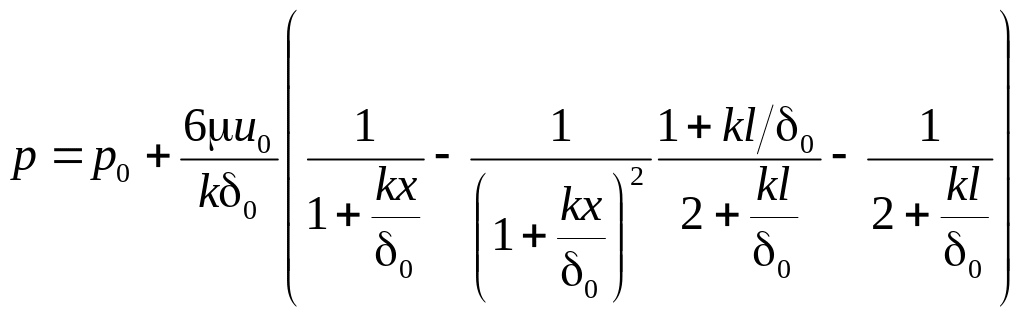(6.18)

Расчеты по этой зависимости показывают, что на всей длине l p>p - Эпюра избыточных давлений приведена на рис. 6.4. Уравнение (6.18) позволяет вычислить величину поддерживающей силы.

6.8. Ламинарное течение в круглой трубе

При установившемся течении жидкости вдоль оси х в горизонтальной трубе u_z= ; X=Y=0; =0, Z=—g. Уравнение (3.10') в проекции на оси х, у, z примет вид

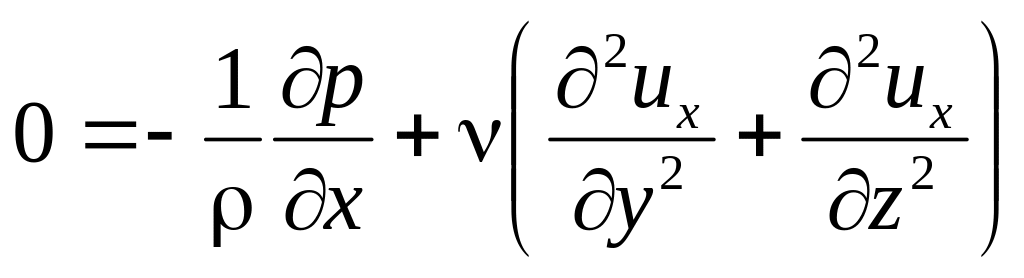, (6.19)

, ,т. е. в живом сечении р =—С(х)— gz и др/дх не зависит от у и z.

При переходе к цилиндрическим координатам (рис. 6.5) получим

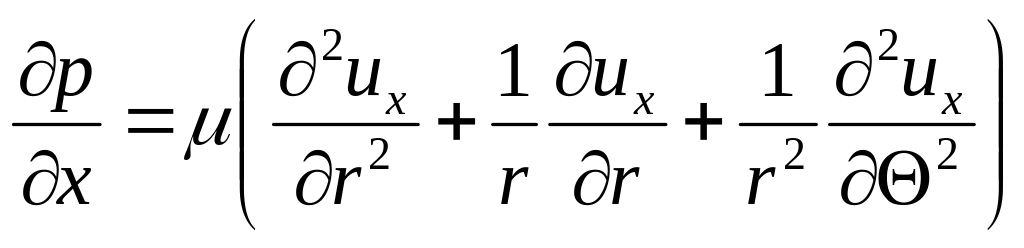. (6.20)

В силу физически очевидной осевой симметрии профиля скоростей =0. С учетом этого (6.20) можно представить так:

. (6.21)

Поскольку производная др/дх не зависит от у и z, то она не зависит и от r. Проинтегрируем (6.21) дважды по r при начальных условиях: при r=0 =0; при r=r₀ =0. Получим

. (6.22)

При r=0

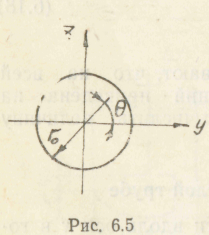(6.23)

Расход жидкости вычислим с учетом (6.22) и (2.5'), приняв ds_n=2 rdr. Получим

. (6.24)

Средняя расходная скорость

. (6.25)

Разделив (6.23) на (6.25), найдем u_m/v=2, a (6.22) на (6.25)—профиль скоростей в безразмерном виде:

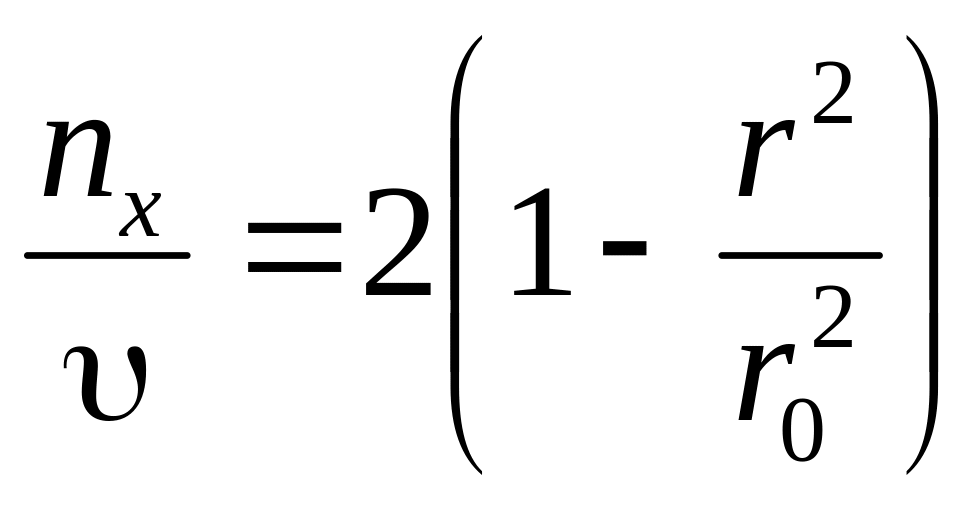(6.26)

Проинтегрируем (6.25) по х, получим

, (6.27)

где d – диаметр трубопровода; p₁ и p₂ - давления в начале и конце трубопровода.

Сопоставьте (6.27) и (6.7).

Для расчета потерь давления в трубах нередко применяется формула Дарси-Вейсбаха (6.12).

Приравняв (6.12) и (6.27), получим выражение для расчета коэффициента гидравлического трения:

(6.28)