6.4. Решение задач гидродинамики методом теории подобия

При интегрировании дифференциальных уравнений в оп­ределенных пределах решение всегда содержит лишь ту или иную комбинацию коэффициентов уравнения и граничные условия.

Поясним это на легко решаемом примере. Дано уравне­ние и начальное условие при x=x₀ у=у₀ . Вычислить y₁ при х =x_1. После введения масштабов x₀ и у₀ и приведения уравнения к безразмерной форме нетрудно най­ти, что решение задачи имеет вид

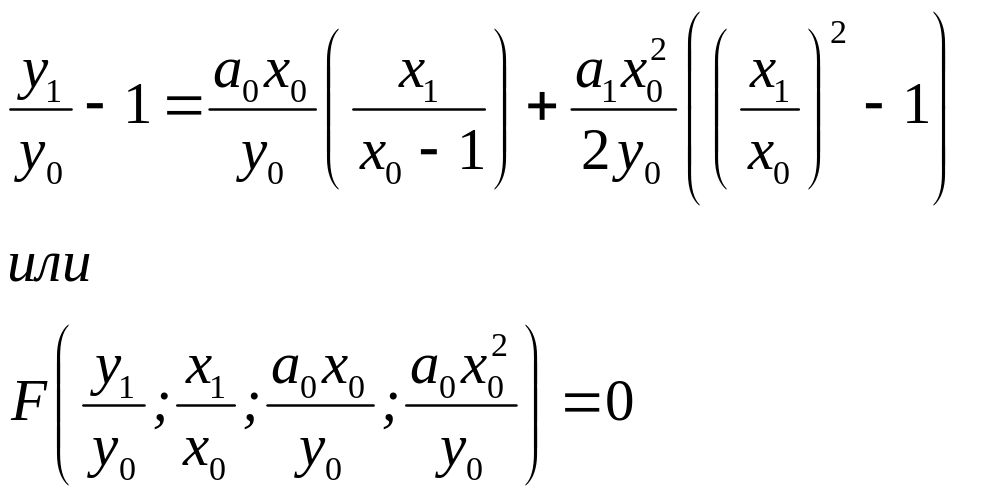
По аналогии можно утверждать, что и решение уравне­ния Навье—Стокса можно записать F(Sh; Fr; Eu; Re; Г₁; Г₂; ...)=О, где Г₁; Г₂ — отношения различных размеров объ­екта к масштабу L, определяющие его геометрию (геометри­ческие симплексы).

Покажем, что применение уравнения движения в безраз­мерном виде существенно сокращает объем эксперименталь­ных исследований, необходимых для уточнения вида искомой функции. Рассмотрим несколько примеров:

а) установившееся ламинарное течение в жидкости в го­ризонтальной трубе. В качестве масштабов при решении этой задачи можно принять L = d, U=v (d — диаметр тру­бы; v — средняя расходная скорость). Поскольку и =0, то уравнение (6.6) существенно упростится и его можно привести к виду

т . е. получим уравнение с одним коэффициентом Eu*Re. Ре­шение следует искать в виде F(Eu*Re; l/d=0), где l — дли­на трубы, или Eu*Re=f(l/d). Физически очевидно, что

~l, т.е. f(l/d) =C и расчетное уравнение содержит только один неизвестный коэффициент С:

(6.7)

б) установившееся турбулент­ное течение в горизонтальной трубе. Если подставить уравнение (3.5) в (6.3) и привести последнее к безразмерному виду, то при

Это уравнение содержит два независимых коэффициента Еu и Re и его решение следует искать в виде (Eu; Re; )=0

или Eu=f(Re) , или

(6.8)

в) установившийся турбулентный режим перемешивания жидкости в аппарате с мешалкой (рис. 6.2). В отличие от предыдущей задачи в уравнении сохраняется слагаемое X и решение следует искать в виде

, (6.9)

где n — число лопастей.

Выберем масштабы: L = d; — средний пере­пад давлений на лопасти. Сила F, действующая на n лопа­стей, пропорциональна , а мощность N на перемеши­вание жидкости N~F d, т. е.

~

С учетом выбранных масштабов числа подобия примут вид

Подставив в (6.9) преобразованное число Еu, решим его относительно k_N

Вид этой зависимости чаще всего раскрывают на основе экспериментальных исследований. Некоторые задачи гидро­механики удается решить точными методами. Рассмотрим простейшие из них.

6.5. Ламинарное безнапорное течение Куэтта

Это установившееся течение жидкости между двух парал­лельных пластин под действием движения одной из них (см. рис. 1.1). В уравнениях (3.10') u_z=u_y=0; X=0; =0; =0. Следовательно, уравнение движения в проекции на ось х примет вид

Интегрируем

Граничное условие: при z=0 , =0, отсюда С₂=0; при

z= u_x = u₀, тогда С₁= .

Итак, распределение скоростей в зазоре, как ранее и предполагалось, линейно и подчиняется зависимости u_x=u₀z/ . Из (3.5) следует, что и так как = const, то ясно, что при течении Куэтта = const ( — касательное напряжение на стенке канала).