6. Общие закономерности динамики вязкой жидкости

6.1. Два режима течения

Опыты, проведенные Рейнольдсом на установке, схема которой представлена на рис. 6.1, позволили установить, что при в трубке наблюдается слоистое, ламинарное те­чение жидкости. Вводимая в поток подкрашенная жидкость

размывается только за счет диффузии. При v>v_кр2>v_кр1 размыв краски происходит практически мгновенно. В потоке наблюдаются пульсации скорости и перемешивание слоев. Такой режим называется турбулентным. В области скоростей v_кр1<v<v_кр2 режим течения может быть турбулентным, ли­бо ламинарным. При увеличении скорости от значений и v<v_кр1 в этой области сохраняется ламинарный режим, а при уменьшении от значений v>v_кр2 — сохраняется турбу­лентный.

Опыты позволили установить, что режим течения зависит не только от v , но и от вязкости и диаметра трубы d. При Re=vd/ >d/v<Re_KP1 = 2320 —ламинарный режим, при Re> >Re_кр2— турбулентный режим. Величина Re_кр2 зависит от условий проведения опытов, от качества исполнения установки, от внесения возмущений в поток. По мере улучшения качества установок число Re_кр2 увеличивалось и составляло 10000, 13800, 50000 и т. д.

В промышленных трубопроводах условия течения жидко­сти далеки от идеальных, всегда присутствуют вибрации установок, пульсации расходов. Это приводит к развитию турбулентности практически при Re Re_кр1. Поэтому при расчете промышленных трубопроводов можно принимать, что при Re 2320 — режим ламинарный, а при Re>2320 — тур­булентный.

При расчете числа Рейнольдса для каналов некруглого сечения диаметр их определяется по формуле , где s_n — площадь живого сечения, — периметр сечения, смо­ченный жидкостью.

6.2. Уравнение турбулентного течения несжимаемой жидкости (уравнение Рейнольдса)

При решении практических задач обычно бывают заданы средние во времени значения скоростей и напряжений , . Уравнение движения, выраженное через и , было выведе­но Рейнольдсом. В качестве исходных возьмем уравнения движения в напряжениях (3.9'). Преобразования выполним для первого из них.

С учетом (2.8) и (2.13) ускорение можно предста­вить в виде

(6.1)

Истинные значения скоростей и напряжений с осредненными связаны зависимостями:

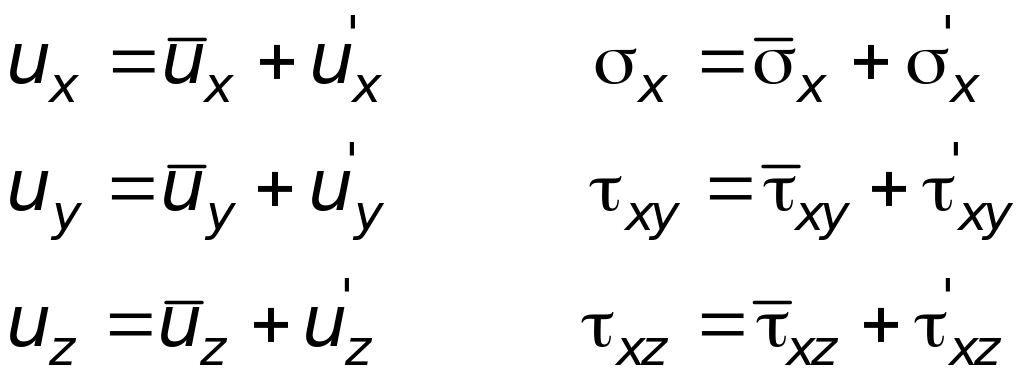(6.2)

Здесь и_х', и_у', u_z', , , - пульсационные состав­ляющие.

Подставим уравнения (6.1) и (6.2) в (3.9') и проведем операцию сглаживания (осреднения) функций по правилам:

если а = +a' и b= +b', то ; ; ; =0; После

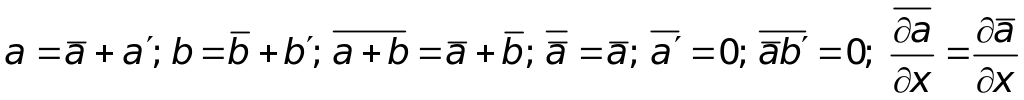
преобразований получим

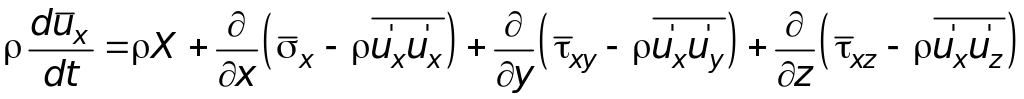(6.3)

Итак, при турбулентном течении жидкости в результате пульсаций скоростей возникают дополнительные или турбу­лентные напряжения. Аналогичные только что приведенным преобразования со всеми уравнениями (3.9') позволяют выявить шесть независимых компонентов турбулентных на­пряжений:

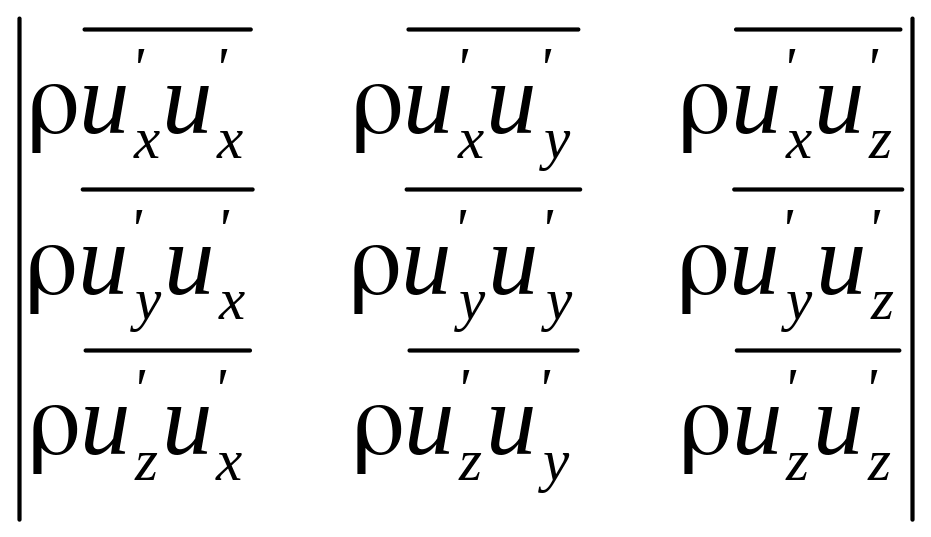(6.4)

Система, состоящая из уравнения Рейнольдса, уравнений (2.13') и (3.5), которые после сглаживания не претерпят из­менений, не замкнута. Для замыкания ее необходимы еще шесть уравнений.

6.3. О моделировании в гидромеханике

Два процесса подобны, если описываются тождественными уравнениями с тождественными граничными условиями и протекают в геометрически подобной обстановке. Зная условия подобия, можно исследовать модельный аппарат, машину, а потом перенести результаты испытаний на реальный проектируемый объект. Для выявления условий гидромеханического подобия преобразуем уравнение Навье—Стокса (3.10') к безразмерному виду.

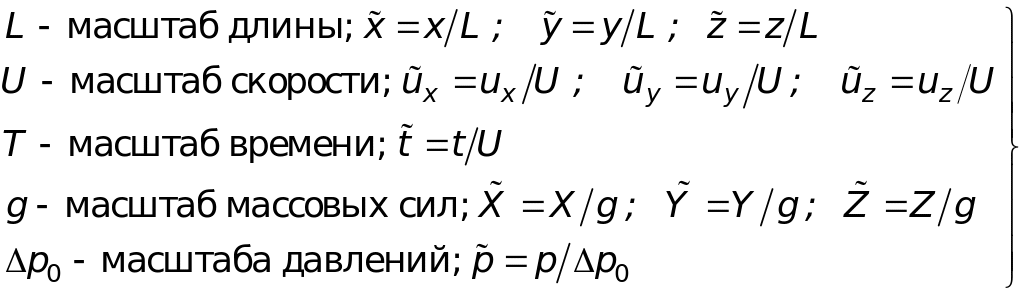(6.5)

Здесь величины, отмеченные волнистой линией, безразмер­ные. Подставим (2.8) в (3.10'). С учетом (6.5) первое из уравнений (3.10') можно представить в виде (после вынесе­ния масштабов из-под знаков дифференциала умножим все слагаемые на L/U²)

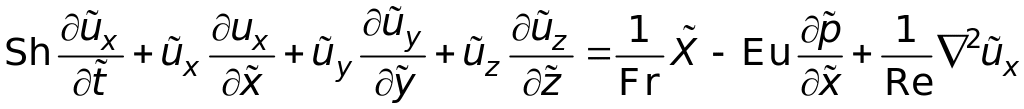, (6.6)

где .

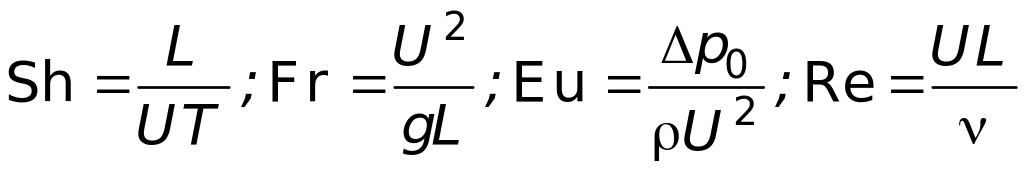Безразмерные коэффициенты Sh, Fr, Eu, Re называются числами подобия (иногда — критериями подобия) и носят имена ученых: Sh— число Струхаля; Fr—число Фруда; Еu — число Эйлера; Re — число Рейнольдса. Равенства чисел подобия в уравнении (6.6) и геометрическое подобие модели и объекта достаточно для обеспечения подобия гидромеха­нических процессов.

Поскольку каждое из слагаемых уравнения Навье—Стокса характеризует одну из сил, действующих в жидкости, то числа подобия характеризуют их отношения. Так,

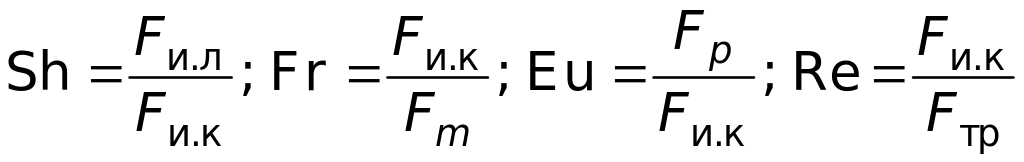,где

F_и._л — сила инерции, вызванная локальным ускорением;

F_и.к — сила инерции, вызванная конвективным ускоре­нием;

F_м— массовая сила;

F_тр — сила вязкостного трения;

Fр — сила давления.

Полную модель для объекта не всегда удается получить.

Например, пусть L₀/L_м =10² (индексы: о – объект; м – модель). Тогда из равенства чисел Фруда U₀²/(gL₀) = U_м²/(gL_м) следует, что U₀/U_м= (L₀/L_м)^0,5=10; из равенства чисел Рейнольдса

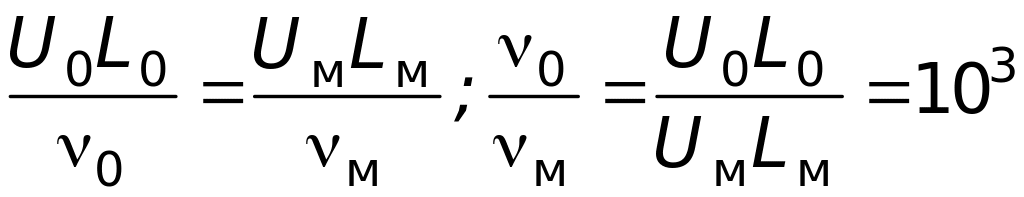
испытания модели надо проводить в среде, вязкость которой значительно ниже вязкости среды объекта, что не всегда удается реализовать.