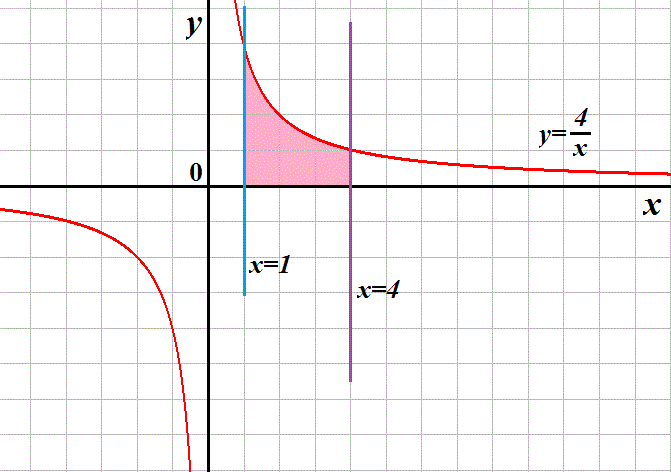
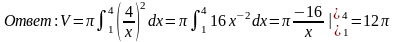- •Дайте опр-я ф-и, а также сложной и обратной ф-й одной действительной переменной. Найдите обл опр и обл значений функции .
- •Сформулируйте св-ва четности, нечетности, периодичности, монотонности, ограниченности ф-и. Определить явл-ся ли след ф-я четной или неч.
- •Дайте определения числовой посл-ти и предела числовой посл-ти. Сфор-те теорему о единственности предела числовой посл-ти.
- •Переч правила вычисления пределов посл-тей. Дайте определение числа e.
- •Дайте определение предела функции. Перечислите основные свойства пределов функций.
- •Дайте определения односторонних пределов функции.
- •Перечислите основные правила вычисления пределов функций.
- •Приведите первый (с доказательством) и второй замечательные пределы.
- •Дайте опр непрерывности ф-и в точке. Сформ-те условия непрерывности сложной ф-и. Что вы можете сказать о непрер-ти основных элем ф-й?
- •Перечислите основные локальные свойства непрерывных функций.
- •Сформ теорему о сущ-и корня уравнения для ф-и , непрерывной на отрезке. Докажите, что уравнение имеет корень на отрезке .
- •Сформ теорему о существовании и непрерывности ф-и, обратной к строго монотонной непр ф-и. Приведите пр-р и обоснуйте его на основании теоремы.
- •Сформулируйте свойства функций, непрерывных на отрезке: об ограниченности функции, о достижении наибольшего и наименьшего значений.
- •Дайте опр производной ф-и в точке. На основании опр-я найди производную ф-и .
- •Приведите правила дифференцирования суммы, разности, произведения и частного двух функций, Докажите одно из них на выбор.
- •Приведите правила дифференцирования сложной и обратной функции. Найдите производную функции согласно сформулированному правилу.
- •Дайте определение производных высших порядков ф-и одного аргумента. Приведите примеры вычисления таких производных.
- •Сформулируйте с обоснованием ответ на вопрос: в чем состоит связь между дифференцируемостью и непрерывностью функции?
- •Обоснуйте возможность использования дифференциала в приближенных вычислениях. Приведите пример.
- •Сфор-те теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
- •Сформ теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
- •Сформ теоремы Ферма и Ролля для дифференцируемых функций. Проверьте справедливость теорема Ролля для функции на отрезке .
- •Сформулируйте правило Лопиталя. Докажите первый и второй замечательные пределы с помощью правила Лопиталя.
- •Дайте определения возрастающей и убывающей функций. В чем состоит необходимое и достаточное условия локального экстремума функции.
- •Дайте определения выпуклых вниз и вверх функций одного аргумента. Приведите достаточные условия выпуклости функции. Приведите примеры.
- •В чем состоит необх и дост признаки точки перегиба графика функции. Приведите пример.
- •Дайте опр-я ф-и двух переем-ых, предела и непрерывности ф-и двух переем-х.
- •Дайте определения частных производных ф-и двух переменных, дифференцируемости ф-и нескольких переем-х и ее дифференциала. Приведите примеры вычисления производных и диф-ла ф-и двух пременных.
- •Дайте опр-я производной по напр-ю и градиента ф-и двух перем. ВчемСостоитОсновное св-о градиента ф-и.
- •Сформулируйте теорему о наибольшем и наименьшем значениях дифференцируемой функции на замкнутом ограниченном множестве. Приведите пример.
- •Дайте опр- частных производных высших порядков ф-и двух перем. Сформ теорему о равенстве смешанных производных и приведите в качестве ее иллюстрации пример.
- •Дайте опр экстремума функции двух переменных. В чем состоит необходимое и достаточное условия экстремума. Проиллюстрируйте это на примере.
- •Дайте опр-я условных максимума и минимума функции двух переменных. В чем состоит метод множителей Лагранжа для нахождения условных максимума и минимума функции двух переменных. Приведите пример.
- •Дайте опр однородной ф-и двух аргументов и сфор теорему Эйлера. Явл-я ли ф-я однородной, и если да, то какова степень одн-ти?
- •Дайте определение выпуклой функции двух аргументов и приведите критерий выпуклости. Проиллюстрируйте это на примере.
- •Дайте определение и перечислите основные свойства неопределенного интеграла, иллюстрируя их примерами.
- •Сформулируйте теорему о замене переменной в неопределенном интеграле и правило интегрирования по частям. Докажите любое из этих двух утверждений.
- •Дайте определение и приведите пример первообразной. Сформулируйте теорему о существовании первообразной для непрерывной функции.
- •Напишите формулы вычисление площади криволинейной трапеции и объема тела вращения. Приведите в обоснование чертежи к каждой из формул и приведите примеры.
- •Дайте определения несобственных интегралов с бесконечными пределами. Приведите примеры вычисления таких интегралов.
- •Сформулируйте определения числового ряда и его суммы. В чем состоит достаточный признак сходимости ряда. Гармонический ряд.
- •Сформулируйте определения и приведите признаки сходимости положительных и знакочередующихся рядов. Проиллюстрируйте это на примерах.
- •Дайте опр степ ряда и обл его сх-ти. Приведите фор-лу для выч-я радиуса сх-ти степ ряда.
Дайте определение и приведите пример первообразной. Сформулируйте теорему о существовании первообразной для непрерывной функции.
1.Функция
F(x)
называется первообразной
для функции
f(x)
на промежутке ХR,
если для любого
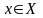 функция
y=F(x)
дифференцируема и выполняется равенство
функция
y=F(x)
дифференцируема и выполняется равенство
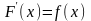
Пример: Непрерывная ф-ция F(x)=sinx - первообразная функции y=cosx на x=(-;+), F’(x)=(sinx)'=cosx
2. Теорема. Если y=f(x) непрерывна на xR, то у нее на х существует первообразная F(x).
Если F(x) первообр ф-и f(x) на xR, то G(x)=F(x)+C(общий вид первообр на х ф-и f(x)
Пример: см. выше
Дайте определение определенного интеграла и приведите формулу Ньютона-Лейбница. Сформулируйте основные свойства определенного интеграла, иллюстрируя их примерами.
Пусть
функция
определена на отрезке
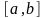 .
Разобьем отрезок на
.
Разобьем отрезок на
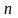 частей точками
частей точками
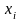 (
( )
такими, что
)
такими, что
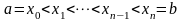 .
Длины полученных отрезков обозначим
.
Длины полученных отрезков обозначим
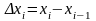 (
(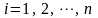 ),
и пусть
),
и пусть
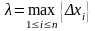 – наибольшая из этих длин. Выберем на
каждом из отрезков разбиения произвольную
точку
– наибольшая из этих длин. Выберем на
каждом из отрезков разбиения произвольную
точку
 и составим сумму
и составим сумму
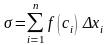 ,
которую назовем интегральной
суммой для
функции
.
,
которую назовем интегральной
суммой для
функции
.
Рассмотрим
интегральные суммы, соответствующие
разбиениям отрезка
при различных значениях
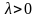 .
Если существует предел таких сумм при
.
Если существует предел таких сумм при
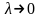 ,
то он называется определенным
интегралом
функции
,
то он называется определенным
интегралом
функции
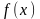 на отрезке
и обозначается
на отрезке
и обозначается
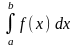 ,
,
2.
Формула Ньютона – Лейбница:
Пусть ф-ция y=f(x)
непрерывна на отрезке [a,b]
и F(x)
– первообразная для f(x).
Тогда
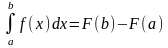
Пример.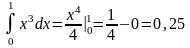
3. Основные св-ва определенного интеграла:
1.
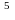
Пример.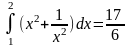
2.
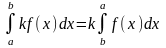 , где k – постоянная.Пример.
, где k – постоянная.Пример. =1
=1
3.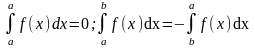
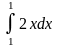 =0;
=0;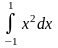
4.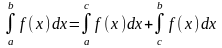 Пример.
Пример.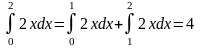
5.если
f(x)g(x)
на отрезке [a,b],
то
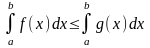
6.если на отрезке [a,b] выполняется mf(x)M,то
m(b-a)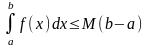 (оценка
интеграла)
(оценка
интеграла)
пример.

M=3/5,m=1/2 на [0;2] c помощью производной
½(2-0) 3/5(2-0)
7.теорема о среднем
Для непрерывной на отрезке[a,b] функции y=f(x) найдется точка с[a,b]
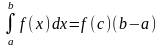
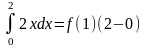
Напишите формулы вычисление площади криволинейной трапеции и объема тела вращения. Приведите в обоснование чертежи к каждой из формул и приведите примеры.
Вычисление площадей плоских фигур.
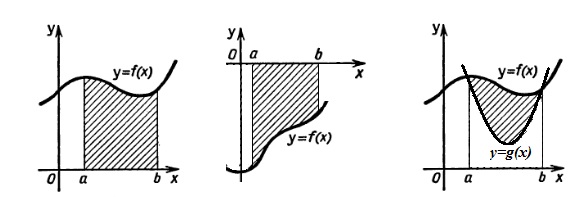
Изв-но, что опред-ый инт на отрезке предст-ет собой площадь криволин трапеции, огран-ой гр-ом ф-и f(x). Если гр расположен ниже оси Ох, т.е. f(x) < 0 (случай 2), то площадь имеет знак “-“, если гр расп выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+” (случай 1).
Для
нахождения суммарной площади используется
формула
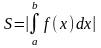 .В
3 случае имеем область, принадлежащую
обеим криволинейным трапециям (как для
верхней, так и для нижней функции). В
данном случае площадь заштрихованной
области – разница площадей трапеций
верхнего и нижнего графиков функций.
.В
3 случае имеем область, принадлежащую
обеим криволинейным трапециям (как для
верхней, так и для нижней функции). В
данном случае площадь заштрихованной
области – разница площадей трапеций
верхнего и нижнего графиков функций.
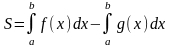
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
И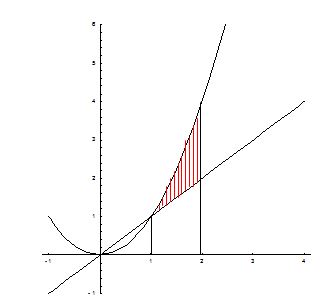 скомая
площадь (заштрихована на рисунке) может
быть найдена по формуле:
скомая
площадь (заштрихована на рисунке) может
быть найдена по формуле:
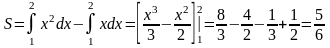 (ед2)
(ед2)
Объем тел вращения. Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что ф-я f(x) непр-на на отре [a, b]. Если соотвую ей кривол трапецию с основаниями а и b вращать вокруг оси Ох, то получим так наз-ое тело вращения.
Т .к.
каждое сечение тела плоскостью x
= const
представляет собой круг радиуса
.к.
каждое сечение тела плоскостью x
= const
представляет собой круг радиуса
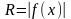 ,
то объем тела вращения может быть легко
найден по полученной выше формуле:
,
то объем тела вращения может быть легко
найден по полученной выше формуле:
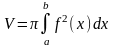
При
вращении вокруг оси Оу
рассуждения аналогичны, только
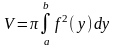 Примечание:
Рисунок тот же только вместо х написать
у.
Примечание:
Рисунок тот же только вместо х написать
у.
Пример:
Вычислить объем тела вращения,
образованного вращением вокруг оси
абсцисс фигуры, ограниченной гиперболой
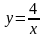 ,
осью абсцисс и прямыми
,
осью абсцисс и прямыми