34. Дайте опр-я производной по напр-ю и градиента ф-и двух перем. ВчемСостоитОсновное св-о градиента ф-и.

Производная по напр-ю —предел df(x₀,y₀)/de^→ =lim_t→0+0 f(x_o+te_x,y₀+te_y)-f(x₀,y₀)/t Произв по напр-ю пок-ет на сколько быстро ф-я изменяется при движении вдоль заданного направления. Так как произв пок-ет скорость изм-я ф-и, то можно сказать, что 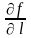хар-ет быстроту изм-я ф-и 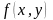по напр-ию 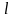в точке 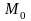. Если напр-е совпадает с полож-ым напр-ем оси Ох, то есть част производная ф-и по х в точке . Если совпадает с полож направлением оси Оу, то есть частная производная функции по у в точке .

f’(M)=F _Y(M)*V₁+F _Y(M)*V₂/

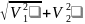
Градиент-вектор, координаты которого равны соответствующим частным производным данной функции в точке M. gradf(m)=(f _x(m);f _y(m)) z=5x³y²-x

Пр. Пусть z=f(x;y) = 3х+5у+6. Тогда grad z = {3_;5} – направл роста ф-и – вектор нормали.

Основное свойство градиента: Вектор-градиент направлен в сторону наискорейшего возрастания функции в данной точке.

grad (C · f) = C · grad f, grad (f + g) = grad f + grad g,

grad (f · g) = g · grad f + f · grad g,

grad f/g = g · grad f − f · grad g/g²

35. Сформулируйте теорему о наибольшем и наименьшем значениях дифферен­цируемой функции на замкнутом ограниченном множестве. Приведите пример.

Пусть ф-я u = f (x₁ , x₂ ,…, x_n) опр-на и непрерывна в нек- огр-ом и замкнутом мн-ве D и имеет на этом мн-ве конечные част производные (за искл, быть может, отд точек). Тогда эта ф-я достигает на D своего наиб и наим зн-я (см. св-ва непрерывных ф-й). Если это знач дост-ся во внутр точке мн-ва, то, очевидно, эта точка д быть стац; кроме того, наиб и наим зн-е может дост-ся на границе мн-ва D. Поэтому для опр-ия наиб и наимо зн-й ф-и на мн-ве D треб-ся:

1. найти стац точки ф-и, принадлежащие D, и выч-ть зн-я ф-и в этих точках; 2)найти наиб и наим зн-е, принимаемое ф-ей на границе мн-ва D;3) выбрать наим и наиб из полученных чисел, кот-е и будут являться наим- и наиб- зн-ми ф-и на всем мн-ве D.

Пример. Найдем наиб зн ф z = sin x + sin y – sin (x + y) в треуг-ке со сторонами х = 0, у = 0, х + у = 2π. Стац точки опр-ся из решения системы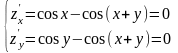 , откуда . Един-ой внутр точкой дан тр-ка, являющейся реш-м получ сис-мы, буде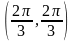т , в кот . Это зн-е оказывается наиб и на всем рассм-ом мн-ве, так как на его границе z = 0.

36. Дайте опр- частных производных высших порядков ф-и двух перем. Сформ теорему о равенстве смешанных производных и приведите в качестве ее иллюстрации пример.

Пусть D – открытое множество в R² , f(x,y) – определенная на множестве D ф-я. Предположим, что в каждой точке М D существуют частные производные f ‘_x и f ‘_y. Тогда частные производные f ‘_x(x,y) и f ’_y(x,y) естественно считать ф-ми с обл опр D Они наз-ся частными производными пер-го порядка. Част производные от ф-й f ‘_x(x,y) и f ’_y(x,y) наз-ся част производными вт-го порядка от ф-и f(x,y). Част производные от част производных вт-го порядка наз-ся част производными т-го порядка и т.д. Если первая производная ф-и z= f(x,y) была взята скажем, по x, то ее частные производные в (x₀,y₀) обозн-ся так:

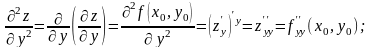
Продолжая дифф-ть полученные рав-ва, получим частные произв более высоких порядков.

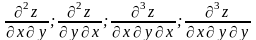
Определение. Частные производные вида и т.д. называются смешанными частными производными.

Теорема. Если производные f_xy(x,y) f_yx(x,y) существуют в некоторой окрестности точки М(x₀,y₀) и непрерывны в самой точке М, то имеет место равенство: .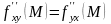

Пример: Док-ть справедливость теоремы (част производные высших порядков не зависят от порядка дифф-ия) для f (x;y) = x³–3y³+5xy²

Проверка: f '_x=3x²+5y² f '_y=10xy–9y² f ''_xy=10y f ''_yx=10y. Теорема спр-ва.