
Введение.
В процессе проектирования глобальной многофункциональной информационно вычислительной сети отраслевого масштаба, охватывающей предприятия отрасли, расположенные в ряде регионов страны, для оценки показателей пропускной способности сети с использованием методов математического моделирования к числу основных задач относится задача сбора и обработки исходных данных для математических моделей сети. В составе исходных данных должны быть определены параметры потоков заявок на обслуживание. Для рассматриваемой проектируемой системы руководство предприятий-пользователей сети представило данные по требуемым объемам информации, которые в течение рабочего дня должны передаваться по определенным направлениям передачи информации в сети и по определенным функциям, выполняемым сетью. Определены были также средние объемы передаваемых файлов по различным направлениям сети и функциям, выполняемым сетью. По каждой функции и направлению сети интенсивность потока заявок определяется формулой:
, (1/сек) (1)
где
V - требуемый объем информации в Кбайт, подлежащий передаче в течение рабочего дня по определенному направлению и функции сети;
Vcp - средний объем передаваемых файлов по определенному направлению и функции сети в Кбайт;
Т - продолжительность рабочего дня (Т = 28800 сек).
В предположении
пуассоновского потока заявок в сети
интенсивность потока заявок  равна параметру потока заявок. Определяемые
параметры
являются фактически максимальными,
поскольку вычислены их требований
пользователей, естественно, предъявленных
в виде максимального запроса. Если у их
использовать в качестве исходных данных
для моделей сети,
равна параметру потока заявок. Определяемые
параметры
являются фактически максимальными,
поскольку вычислены их требований
пользователей, естественно, предъявленных
в виде максимального запроса. Если у их
использовать в качестве исходных данных
для моделей сети,
то примерно в 50 %
случаев передаваемые объемы информации
превысят требуемые значения. Для того,
чтобы получить их этих данных исходные
данные для моделирования системы, должно
решиться следующее уравнение относительно
параметра  :
:
 , где
(2)
, где
(2)
k = [ m Т];[…]— округление до целого числа. Параметр потока заявок , вычисленный путем решения уравнения (2), обеспечивает при имитации потока заявок в течение рабочего дня превышением числом заявок величины К в 1 % случаев.
Соотношение (2) является точным. Левая часть уравнения (2) является функцией распределения вероятностей случайной величину распределенной по закону Пуассона, и изменяется монотонно, относительно параметра . Поэтому для решения уравнения (2) относительно был применен метод последовательных приближений (метод половинного деления), обеспечивающий однозначное решение с заданным числом верных цифр.
В связи с затратой машинного времени целесообразно исследовать возможность использования для практических расчетов приближенной формулы:
где (3)

Приведенная
приближенная формула может использоваться
при больших значениях  «для грубых, ориентировочных расчетов».
Возможность использования правой
части приближенного равенства (3) в
качестве левой части уравнения (2) и
получения при этом решения уравнения
(2) с заданным числом верных цифр не
исследована. Таким образом, область
возможного использования соотношения
(3) в рамках рассматриваемой научно-технической
задачи не определена. В дальнейшем
уравнение (2) будет именоваться точным
соотношением, а приближенным
соотношением будем именовать уравнение
(2), когда в качестве левой его части
использована правая часть уравнения
(3).
«для грубых, ориентировочных расчетов».
Возможность использования правой
части приближенного равенства (3) в
качестве левой части уравнения (2) и
получения при этом решения уравнения
(2) с заданным числом верных цифр не
исследована. Таким образом, область
возможного использования соотношения
(3) в рамках рассматриваемой научно-технической
задачи не определена. В дальнейшем
уравнение (2) будет именоваться точным
соотношением, а приближенным
соотношением будем именовать уравнение
(2), когда в качестве левой его части
использована правая часть уравнения
(3).
2. Постановка задачи на исследование.
При заданных величинах Т и Р (Т>0, 0<Р<1, Р - правая часть уравнения (2), где для решения изложенной научно-технической задачи оно заданно равным 0, 99) разработать алгоритм и программу для ПЭВМ решения уравнения (2) относительно параметра с заданным числом верных цифр (s) в результате и при практических затратах машинного времени.
Приближенное число может быть представлена в следующем виде:
 ,
,
где
 -
i-я
значащая цифра
(в числе значащих цифр не включаются
предшествующие
-
i-я
значащая цифра
(в числе значащих цифр не включаются
предшествующие  нули;
|
|>0);
нули;
|
|>0);
r - порядок первой значащей цифры;
s - число значащих цифр в ,
s значащих цифр в являются верными, если выполнено неравенство:
 ,
,
где
| |
- абсолютное значение погрешности числа
|
- абсолютное значение погрешности числа
|
| = | -
- |, где
-
точное значение величины, характеризуемой
приближенным числом
.
|, где
-
точное значение величины, характеризуемой
приближенным числом
.
3. Результаты исследовательских расчетов.
Д
ъ>
ля решения точного соотношения, как уже упоминалось, применен метод последовательных приближений (метод половинного деления). На первом шаге величина делится пополам, и результат подставляется в левую часть соотношения (2) в качестве параметра . Если при этом левая часть соотношения (2) оказывается меньше правой, то для последующего деления пополам на следующем шаге берется интервал (0, /2). Если же левая часть соотношения оказывается больше правой, то для после- дующего деления пополам выбирается интервал ( /2,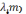 .
.
Подобная процедура
осуществляется на всех последующих
шагах расчета, до тех пор, пока у выбранного
на следующем шаге интервала( )
абсолютная разность границ не обеспечит
выполнения неравенства:
)
абсолютная разность границ не обеспечит
выполнения неравенства:
|  |<0,5
|<0,5 .
.
Округленная до s
значащих цифр величина 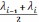 является результатом расчета, который
обозначим через
является результатом расчета, который
обозначим через  ,
с s
верными значащими цифрами. Путем
элементарных преобразований приближенного
соотношения получена следующая
расчетная формула:
,
с s
верными значащими цифрами. Путем
элементарных преобразований приближенного
соотношения получена следующая
расчетная формула:
 } (4)
} (4)
где
tp - квантиль нормального распределения вероятностей N(0, 1) для уровня вероятности Р (в нашем случае Р=0,99).
При выводе формулы
использовалось естественное условие
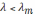 .
Результат расчета по формуле (4) в
дальнейшем будем обозначать
.
Результат расчета по формуле (4) в
дальнейшем будем обозначать
Порядок пересчета
совокупности параметров {  }
в исходные данные для моделирования
должен предусматривать пересчет, начиная
с наименьшего значения
}
в исходные данные для моделирования
должен предусматривать пересчет, начиная
с наименьшего значения  затем
затем  т.д. до
т.д. до  (r
- общее число параметров). Пересчет
должен вестись с использованием точного
соотношения, обеспечивающим определение
соответствующих величин
,
и приближенной формулы вплоть до
(r
- общее число параметров). Пересчет
должен вестись с использованием точного
соотношения, обеспечивающим определение
соответствующих величин
,
и приближенной формулы вплоть до
 ,
и достигается равенство заданного
числа s
первых цифр. При пересчете величин
,
и достигается равенство заданного
числа s
первых цифр. При пересчете величин 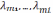 в качестве результата должны выдаваться
соответствующие величины
.
При пересчете величин
в качестве результата должны выдаваться
соответствующие величины
.
При пересчете величин  должна использоваться только приближенная
формула и в качестве результатов
должны выдаваться соответствующие
величины
должна использоваться только приближенная
формула и в качестве результатов
должны выдаваться соответствующие
величины
Предложенный
порядок расчета предполагает
справедливость следующего утверждения:
При  число совпадающих
число совпадающих
первых значащих
соответствующих цифр в величинах
и неограниченно (вплоть до бесконечности)
ступенчато возрастает при монотонном
характере этого возрастания.
Сформулированное утверждение
нуждается в обосновании. Из
следует, что и  .
.
Непосредственно из формулы (4) следует при монотонном характере изменения . Из точного соотношения
(2) следует, что при
любом значении
при стремлении его к бесконечности
соответствующее значение величины К
продолжает оставаться квантилью
распределения Пуассона с фиксированным
уровнем вероятности Р (Р = 0,99). Квантиль
при фиксированном уровне вероятности
может стремиться к бесконечности
только тогда, когда математическое
ожидание и дисперсия распределения,
т.е. произведение
• Т стремиться к бесконечности,
причем монотонно по отношению к величине
К. Поскольку Т есть величина фиксированная,
то имеем:  .
.
В соответствии с
известным утверждением о том, что при
 распределение Пуассона асимптотически
нормально, причем безотносительно к
величине К, должно выполняться следующее
соотношение:
распределение Пуассона асимптотически
нормально, причем безотносительно к
величине К, должно выполняться следующее
соотношение:
 . (5)
. (5)
Отметим, что отношение квантили распределения Пуассона К с уровнем вероятности Р к квантили ненормированного и нецентрированного распределения К+0,5 с тем же уровнем вероятности Р монотонно стремиться к единице:
 .
.
Квантили при
фиксированном Р связанны монотонной
функциональной зависимостью с параметрами
 распределений вероятностей. Поэтому
отношение /
из соотношения (5) должно характеризоваться
монотонным, (хотя и ступенчатым)
характером изменения при стремлении
к пределу. Из соотношения (5) непосредственно
следует соотношение для относительной
погрешности приближенной формулы:
распределений вероятностей. Поэтому
отношение /
из соотношения (5) должно характеризоваться
монотонным, (хотя и ступенчатым)
характером изменения при стремлении
к пределу. Из соотношения (5) непосредственно
следует соотношение для относительной
погрешности приближенной формулы:
 . (6)
. (6)
П
А„,
ричем относительная погрешность характеризуется монотонным характером ступенчатого изменения при стремлении к пределу. Соблюдая осторожность следует допустить возможность стремления к бесконечности абсолютной погрешности | при . Тогда из (6) следует, что бесконечно малаявеличина 1/ как и 1/ при есть величина более высокого порядка малости, чем бесконечно малая величина 1/| |. Следовательно при более быстром возрастании и () по сравнению с абсолютной погрешностью возрастание порядка
первых значащих
цифр r
в числах
и  и при фиксированном требуемом числе
совпадающих первых значащих цифр s в
числах
и приводит к такому росту допустимой
абсолютно погрешности, что она при
конечном
неизбежно превышает фактическую
абсолютную погрешность приближенной
формулы: ||<
0,5
.
Это выполняется при любом конечном
заданном числе s. Конечно для невозрастающей
абсолютной погрешности обоснованное
утверждение будет заведомо справедливым.
Невыполнение изложенных условий при
обосновании сформулированного утверждения
неизбежно приводит к отрицанию
асимптотической нормальности распределения
Пуассона исследовательских
расчетов.
и при фиксированном требуемом числе
совпадающих первых значащих цифр s в
числах
и приводит к такому росту допустимой
абсолютно погрешности, что она при
конечном
неизбежно превышает фактическую
абсолютную погрешность приближенной
формулы: ||<
0,5
.
Это выполняется при любом конечном
заданном числе s. Конечно для невозрастающей
абсолютной погрешности обоснованное
утверждение будет заведомо справедливым.
Невыполнение изложенных условий при
обосновании сформулированного утверждения
неизбежно приводит к отрицанию
асимптотической нормальности распределения
Пуассона исследовательских
расчетов.
МИРЭА
ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
БАЗОВАЯ КАФЕДРА МОИС
при ФГУП ЦНИИ <<ЦЕНТР>>
УТВЕРЖДАЮ:
Заведующий базовой кафедрой
_____________В.Г.Артюхов
<<___>>___________2012г.
