
- •Предмет молекулярной физики. Основные положения молекулярно- кинетической теории. Идеальный газ.
- •2.Законы идеального газа. Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона). Физический смысл универсальной газовой постоянной.
- •4.Степени свободы молекул идеального газа. Теорема Больцмана о распределении энергии по степеням свободы молекул идеального газа.
- •5.Распределение молекул идеального газа по скоростям (распределение Максвелла). Графическое представление и анализ функции распределения.
- •6. Скорости молекул идеального газа (наиболее вероятная, среднеарифметическая, среднеквадратичная)
- •7. Опыт Штерна
- •8. Идеальный газ во внешнем силовом поле. Барометрическая формула.
- •9.Распределение Больцмана.
- •10.Предмет термодинамики. Термодинамическая сила.
- •11. Равновесные и неравновесные состояния.
- •12. Равновесный процесс.Работа при изменении состояния идеального газа.
- •16.Теплоемкость идеального газа при постоянном объеме.
- •17. Теплоемкость газа при постоянном давлении
- •18. Первый закон термодинамики применительно к изопроцессам. Работа идеального газа в этих условиях.
- •19. Адиабатический процесс
- •2 0.Первый закон термодинамики применительно к адиабатическому процессу . Работа идеального газа при адиабатическом процессе.
- •21.Круговые процессы(циклы) кпд кругового процесса.
- •22.Обратимые и необратимые процессы.
16.Теплоемкость идеального газа при постоянном объеме.
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
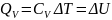
|
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для
процесса при постоянном давлении первый
закон термодинамики дает:

|
где ΔV –
изменение объема 1 моля идеального газа
при изменении его температуры на ΔT.
Отсюда следует: ![]()
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
pV = RT, |
где R – универсальная газовая постоянная.
При p = const
|
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
Cp = CV + R. |
17. Теплоемкость газа при постоянном давлении
Согласно определению теплоемкости при постоянном давлении Ср Qp = СрΔТ.
Работа, которую совершит 1 моль идеального газа, расширяющегося при постоянном давлении, равна A' = RΔT.
Это следует из выражения для работы газа при постоянном давлении А' = pΔV и уравнения состояния (для одного моля) идеального газа. pV = RT.
Внутренняя энергия идеального газа от объема не зависит. Поэтому и при постоянном давлении изменение внутренней энергии ΔU = CVΔT, как и при постоянном объеме. Применяя первый закон термодинамики, получим СрΔТ = CVΔT + RΔT.
Следовательно, молярные теплоемкости идеального газа связаны соотношением Cp = Cy + R.
Впервые эта формула была получена Р. Майером и носит его имя.
В случае идеального
одноатомного газа
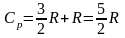
18. Первый закон термодинамики применительно к изопроцессам. Работа идеального газа в этих условиях.
Первый закон термодинамики позволяет вычислить изменение параметров идеального газа при тепловых и механических процессах.
Так, если в газе протекают изопроцессы, первый закон термодинамики может быть записан в частном виде.
При изотермическом процессе изменения внутренней энергии в идеальном газе не происходит и все подводимое к газу количество теплоты идет на совершение им работы. T = const, U = const, ΔU = 0, Q = A
При изохорном процессе объем газа остается постоянным. Соответственно, не совершается работа и внутренняя энергия газа изменяется исключительно за счет теплообмена с окружающей средой. V = const, ΔV = 0, A = 0, ΔU = QV
(Индекс V означает, что процесс протекает при постоянном объеме).
Если при теплообмене происходит изменение температуры газа на ΔT, то QV = cVmΔT. cV – удельная теплоемкость газа при постоянном объеме.
Подставляя
это выражение в уравнение первого
закона термодинамики для изохорного
процесса, имеем: ΔU = cVmΔT.
С другой стороны, для одноатомного
идеального газа ![]()
Приравняв
правые части уравнений и произведя
соответствующие преобразования, имеем:
![]()
При изобарном процессе изменение внутренней энергии газа происходит как за счет теплообмена, так и за счет совершения механической работы. Если к газу подводится некоторое количество теплоты, то оно частично расходуется на увеличение внутренней энергии газа, частично на совершение газом работы при его расширении. p = const, A = pΔV, Qp = ΔU + pΔV.
|
(Индекс p означает, что процесс протекает при постоянном давлении).
Давление газа остается постоянным за счет соответствующего изменения объема. Так как ΔU = QV, то Qp = QV + pΔV.
Таким образом оказывается, что для повышения температуры газа на одно и то же количество градусов при постоянном давлении надо сообщить ему большее количество теплоты, чем при постоянном объеме, так часть теплоты расходуется на совершение работы.
Если
обозначить удельную теплоемкость при
постоянном давлении cp,
то первый закон термодинамики для
изобарного процесса примет вид: ![]() или:
или: ![]() Из уравнения Менделеева–Клапейрона
следует, что
Из уравнения Менделеева–Клапейрона
следует, что ![]() Таким образом,
Таким образом, ![]()
С
учетом того, что ![]() Наряду с удельными теплоемкостями газа
при постоянном объеме и постоянном
давлении cV и cp,
можно ввести молярные теплоемкости CV = cVM при
постоянном объеме и Cp = cpM при
постоянном давлении. Сделав это,
имеем: Cp = CV + R.
Полученное уравнение носит название
уравнения Майера. Кроме рассмотренных,
возможен еще вариант, когда термодинамическая
система не обменивается теплотой с
окружающей средой. Процесс, происходящий
при этом с газом, называется адиабатным.
При адиабатном процессе работа
совершается газом за счет убыли его
внутренней энергии, либо наоборот, за
счет совершения над газом работы,
увеличивается его внутренняя
энергия. Q = 0; A = –ΔU.
Наряду с удельными теплоемкостями газа
при постоянном объеме и постоянном
давлении cV и cp,
можно ввести молярные теплоемкости CV = cVM при
постоянном объеме и Cp = cpM при
постоянном давлении. Сделав это,
имеем: Cp = CV + R.
Полученное уравнение носит название
уравнения Майера. Кроме рассмотренных,
возможен еще вариант, когда термодинамическая
система не обменивается теплотой с
окружающей средой. Процесс, происходящий
при этом с газом, называется адиабатным.
При адиабатном процессе работа
совершается газом за счет убыли его
внутренней энергии, либо наоборот, за
счет совершения над газом работы,
увеличивается его внутренняя
энергия. Q = 0; A = –ΔU.
