27. Уравнение теплопроводности для случаев сферической и цилиндрической симметрии.

Если среда и распределение темп-ры в ней обладают сферической и цилиндрической симметрией, вместо прямоугольной системы координат более удобно использовать сферическую или цилиндрическую координатные системы.

Тогда ур-е тепл-ти записывается для случая сферической симметрии:

; (1), где r – радиус сферы.

Для случая цилиндрической системы: 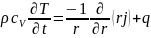; 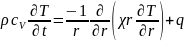(2), где r – расст-е до оси симметрии.

Все задачи на тепл-ть могут быть разделены на стационарные и нестационарные. Стационарным называются такие задачи, в к-х темп-ра Т не меняется во времени. .

26. Теплопроводность. Вывод уравнения теплопроводности в общем виде. Принцип суперпозиций.

Если в твердом теле сущ-т разность темп-р между различными его частями, то тело переносится от более нагретой части к менее нагретой путем теплообмена. В отличие от жидкостей и газов, в твердом теле не может возникнуть конвекция, т.е. перемещение массы в-ва вместе с теплом. Поэтому перенос тепла в твердом теле осуществляется только теплопроводностью. При рассмотрении математич теории теплопроводности, основы к-й были заложены франц математиком Фурье в первой четверти 19 века, предполагается, что: 1) потерями тепла на лучеиспускание можно пренебречь; 2) объем системы остается постоянным, так что никаких перемещений в-ва в процессе передачи тепла не возникает; 3) рассмотрение ограничивается только одномерными задачами, когда темп-ра тела, помимо времени, зависит только от одной пространстввенной координаты.

Плотностью потока тепла назыв вектор j, совпадающий по направ-ю с направ-ем распространения тепла и численно равный кол-ву тепла, проходящему в единицу времени через единичную площадку, перпендикулярную к направ-ю потока тепла. J=σQ/SdT (1) плотность потока тепла.

Пусть в неограниченной среде имеется поток тепла в направ-и, параллельном оси Х. Выделим мысленно в среде цилиндр и рас-ри бесконечно малый участок такого цилиндра АВ с длиной dx. РИС из лаб.раб. 3.1. Пусть S – площадь поперечного сечения цилиндра. Кол-во тепла, поступающее в цилиндр АВ за время dt через основание А с координатой х, равно j(x)Sdt. Кол-во тепла, уходящее за то же время через основание В, будет j(x+dx)Sdt. Полное кол-во тепла, вступающее за время dt в рассматриваемый участок цилиндра, равно

. С др стороны, это кол-во тепла можно представить в виде: σQ=dMc_vdT, где dM=роSdx – масса цилиндра АВб с – уд теплоемкость, dT – повышение темп-ры. Приравнивая оба выраж-я, получаем: . Рас-рим случай бесконечной однородной пластинки толщиной l. Пусть на одной стороне пластинки поддерживается темп-ра T₁, а на другой – Т₂, причем Т₁>T₂. Опыт показывает, что поток тепла пропорционален разности темп-р Т₁-Т₂ и обратно пропорционален толщине пластинки l, т.е. , где χ – коэф-т теплопроводности. Для бесконечно тонкой пластинки примем, что l=dx, T₁=T(x), T₂=T(x+dx). Тогда: . След-но: (2) – ур-е теплопроводности. Если в среде есть источники тепла (например, тепло может выделяться в результате прохождения электрич тока или радиоактивного распада), то для их учета вводится величина q,равная кол-ву тепла, выделяемому источниками в единице объема среды в одну секунду. Тогда ур-е тепл-ти запишется в виде: .

Ур-е тепл-ти (2) линейно и однородно. Пусть Т₁(x,t), T₂(x,t),… - к-л решения ур-я тепл-ти, т.е. выполняются ур-я:

…

Из этого ур-я следует, что и нек-е Т=Т₁+Т₂+…также явля-ся решением ур-я тепл-ти.

Принцип суперпозиций: Если Т₁(x,t), T₂(x,t) и т.д. к-л возможные распределения темп-ры в среде, то их сумма Т= Т₁+Т₂+…также дает нек-е возможное распределение темп-ры в этой же среде.

Знач-е принципа супер позиций: он позволяет по известным решениям ур-я тепл-ти конструировать новые решения ур-я.